I will discuss my experience during the development of the game Super Farter, how a simple game idea turned out to involve somewhat complex mathematics and at least some degree of understanding the psychology needed to keep a player hooked on.

A little about the game

The idea of the game was to create a funny fast-paced game that would be relaxing to play, that is, no constant awareness is required from the user. The target audience was chosen to be children aging 5 - 10, since they represent a strong consumer group on the market. The game is a simple one-button 2D endless runner: tap to jump, hold to fart (fly). The element of farting was added to attract the target audience (hey, say "fart" to a 5 year old, he will start laughing). A unique feature of the game is the concept of speed jumping: by continous jumping (hopping), the player accelerates with either limited or no bounds on speed. Due to the fast-pacedness of the game two distinct problems arise: placing platforms and placing pick-ups on appropriate positions.

Problem #1: Placing platforms

A fast-paced platform runner seems simple enough? Accelerate the character, disperse around platforms and pick-ups, and voilà! Well, it does not turn out to be this simple.
Most mobile phone screens are comparatively small, so a character on the screen ideally should not be particularly small (ideally at least ⅛ of the screen's height).

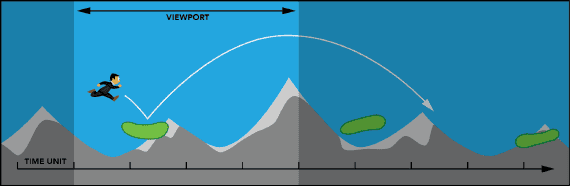
Figure 1: Reaction time vs Viewport size

The problem boils down to reaction time (RT). As we are talking about fast-paced games, the scenary should be scrolling fast. Notice on Figure 1 that the player does not see much of the world ahead, which disables the player to make a decision (e.g. full jump, partial jump, no jump) in time to reach the platform. 

Human RT is about 200 ms at constant awareness. Playing a game in constant awareness is psychically demanding, so we wish to reduce reaction time to about 400-500 ms. The response time is defined to be the the reaction time + movement time. So lets say a player is running along and sees a platform on the right-hand side of the screen, while the world is scrolling left. The movement time of the character takes about 200 ms, the whole process should take about 650 ms on average.

A simple calculation shows that the world should scroll (or equivalently, the player should run) at a speed about

1 screen-width / 0.65 s = 1.5  screen-widths per second,

which is not particularly fast.

In short, a fast-paced 2D platformer does not allow the player to react to visual stimuli within his reaction time.

There are two classical solutions to fix this problem:

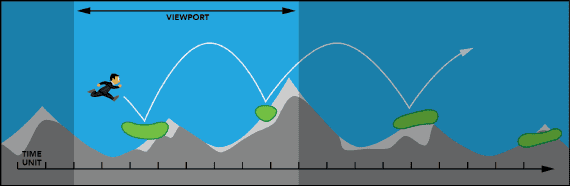
Figure 2: Jumping on platforms at a slower pace

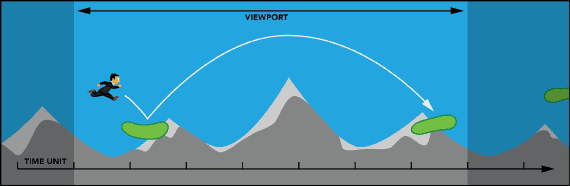
Figure 3: Zooming out making the viewport bigger

Since we are concentrating on fast-paced games, we dismiss the first solution. The second solution would make the player to appear relatively smaller on screen, would keep the physical pace, but would reduce the perceived pace: look at a speeding train at a 10 foot distance or at a 100 foot distance, the train would appear to be much slower (or at least less exciting to watch) in the latter.

A solution to the problem is to make the world dynamic, i.e. let the world adjust to the players decisions. When a player makes a jump, artificially place the platform right where he is supposed to land. Initially this means that the player must take a leap of faith, but as the player recieves a positive feedback at each leap, this brings, on the long run, positive reinforcement to the player: a combined feeling of "I am lucky" and "I am good at this". After a few successful jumps, the player starts to take perfect jumps for granted and does not percieve the fact that the platforms are not visible before the jump, which solves the problem specified.

Lets dig into the mathemacal part of the platform-placing problem. The calculation of the players path can be calulated either by the equations of motion or any method of extrapolation made at the beginning of the jump.

Normaly the equations of motion would seem to be the best choice. Unfortunally preliminary experiments showed that they did not turn out to predict the players movement very good for one or more of the following reasons:

Extrapolation is the best choice in this case. Since the equations of motion still predict a parabolic path, we use quadratic approximation, i.e. find the best 2nd degree polynomial that best fits the player's trajectory and calculate the landing point.

There are two ways to get such a polynomial:

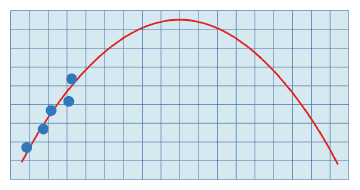
Figure 4: Second degree polynomial approximation

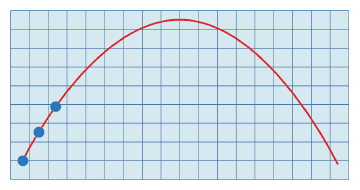
Figure 5: Second degree polynomial interpolation

The approximation method brings good results. The Least Squares Method is a simple widely used algorithm that calculates the best-fitting curve to a given set of points (it can be applied to any type of curve). Once you get the polynomial p(x)=ax²+bx+c that describes your path, simply calculate the solution of the equation p(x)=h, where h is your height at jump-point. The biggest of the two solutions is the x-coordinate of the landing point T to which we move (or create) the platform (Figure 6).

T = (-0.5(b + sqrt(b² - 4ac - 4ah)) / a, h) 
 

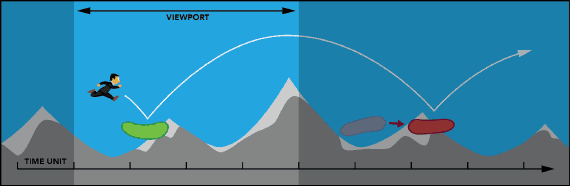
Figure 6: Dynamically placing a platform

Polynomial interplation also brings good results, but not great: is it more susceptible to perturbations, initial inaccuracies in the physics engine.

Drawbacks

If the player makes a bad jump or starts the jump at a slow pace, the jump destination is still in the current viewport and since platforms cannot appear from thin air, the player’s "leap of faith" fails and will provide a negative reinforcement. Thus, a bit of practice may be required from the player.

Problem #2: Placing pick-ups

An analogue problem to the one above appears in placing pick-ups.

Classicaly objects are scattered around the world so that the player can jump to pick them up within his reaction time. Again, a fast-paced game disables the user to acieve this naturally (Figure 7).
 

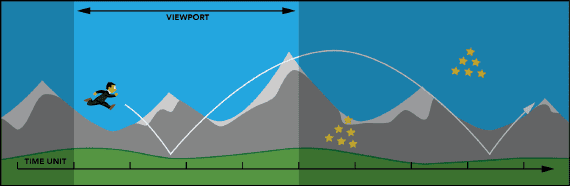
Figure 7: The player misses the pick-ups outside the viewport

We wish that the user, at least most of the time, picks up an object at his peak point, i.e. the vertex of his parabolic jump trajectory (and perhaps also at the landing point), see Figure 8.

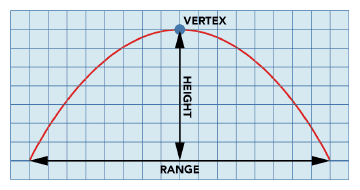
Figure 8: The range, height and vertex of a jump

The previous solution cannot be applied to this case, since the length of a jump is usually between one or two viewport widths, thus, at the jumping time the vertex often appears inside the viewport and the object obviously cannot be placed there mid-game.
A classical solution would again involve to either slow the pace of the game or resize the viewport, but as argued before, this would ruin the fast-pacedness of the game.

We again work out a dynamic solution. Because of the nature of the game (continous jumping), we predict that if the player jumps a few times in a row, the player will jump a few times more. To place pick-ups on the desired places we must predict the players jumping behaviour: we wish to predict the players range and height to get the verticies of the player's next few jumps (Figure 9). Recall that a single jump is bounded by the equations of motion, furthermore, the players trajectory bahaves as a trajectory of a projectile.

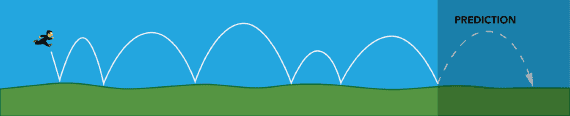
Figure 9: Predicting a jump

The first method that comes in mind is to take an average (arihmetic mean) of the players last n ranges and heights, and take this average to predict the next few jumps. A slightly more advanced method would take a weighted arithmetic mean, since the player is more likely jump a bit more like the previous jump, not the jump made a while ago.

The mean method brings good results but not perfect. Analysis showed that jumps now and then appear to be too imperfect to get a good average. Frequent "bad jumps" appear from one of the following reasons:

On the other hand it might happen that a jump is unusually good. All these irregularities mess up the average.

Trying out various methods, it turned out that outlier ellimination method gave best results. The idea is simple: from the last n jumps, take out m < n jumps that stand out the most and take the average of the remaining. Best three our of five gave satisfying results. In addition, if the player is accelerating on each jump, the range of the jump should be multiplied by a calibrated constant. Now we just  place the pick-up either at the vertex or the landing point of the predicted jump (Figure 10).

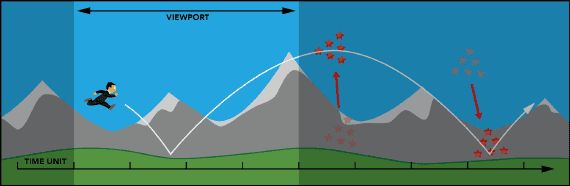
Figure 10: Dynamically placing pick-ups

In the realization the outlier method actually worked too well: collecting practically every item had a very unnatural feeling to it. It did not manage to fool the player into a "I am good at this" feeling. One can easily fix this by randomly scattering around about ⅓ of the pick-ups . With this the player gets a feeling "eventhough items are randomly placed, manage to collect most of them". 

Conclusion

We have discussed two problems that can appear in fast-paced platform games: placing platforms and placing pick-ups so the player hits them every time. We outlined various solutions and pointed out which of the solutions gave the best empirical results. The problems described are imperative only if we wish to place items in favour of the player and win the player over in the sence that the game is enjoyable to play despite the fact that the player is not consciously aware of the deceptions. By fooling the player into thinking he is good at the game, we bring positive emotions and potentially make a game "addictive", which we assume is objective to all game developers. Of course other obsticles (enemies, spikes, rockets,...) should be placed to distract the player and allow the player to eventually lose the game.

You are invited to download and checkout the whole game: Super Farter: a semi-realistic farting simulator.