The RLD Handbook: Sometimes it's not about the metrics - Depth & Complexity

Depth versus Complexity

I recently acquired an arcade cab that came with two games, one of which being Sega’s Decathlete.  A mid 90s take on the classic ‘waggle game’. A type of game (I intentionally didn’t say genre) that is probably best epitomized by California Games - the famous keyboard breaker from the late 80s. Decathlete is one of the least complex games you can get. Rules are simple, interaction is limited but is it a deep game? This got me thinking about the concept of Depth versus Complexity aspect of game design. What tools do we have to evaluate depth and complexity?  How much of either is too much?

To delve into this one, I’m going to look at two games from the same developer which have the same mechanics but different levels of complexity; Radiant Silvergun and Ikaruga. Before I jump into the analysis, I’m going to clarify a few points starting with looking at depth and complexity in relation to mechanics, rules & systems.

Mechanics are actions enacted by game agents (either AI or Human) within the boundaries of the game rules in order to alter game systems to their advantage. I consider what a player can do (game input options) as part of mechanics. The second part of my definition of mechanics is how these inputs are used in specific combinations to achieve an outcome. Therfor the complexity of mechanics is a consequence of the options available to the player and the depth of the mechanics is how many of these 'options' need to be strung together to form the of tactics. 

Mechanics have complexity and depth, but so too can rules and systems.. This means that we can games with low complexity and singificant depth, or any variation of those two things. Given that the games I’ve chosen to examine are arcade games, I am going to presume that they will most likely be low complexity but with significant depth in either the mechanics, systems or both.

As part of this article, I also want to explore the cognitive side of depth and complexity. Is there a difference between high complexity and great levels of depth?  To get the ball rolling, I’m going to start by examining the ubiquitus Rock, Scissors, Paper (RSP).

Rock, Scissor, Paper

In a game of RSP, the player has a clear set of rules. These rules are not complex as there are very few of them and they remain constant.

The ‘system’ behind RSP is best described as a graphic but is also easily described as an IF, THEN, ELSE statement. Given that there are not multiple layers of inter-dependant systems feeding each other, RSP’s systems are not complex.

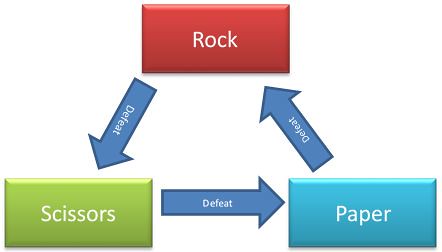
IF Player A chooses ROCK and Player B chooses ROCK THEN Re-Match ELSE

                IF Player A chooses ROCK and Player B chooses SCISSORS THEN Player A wins round ELSE

                IF Player A chooses ROCK and Player B chooses PAPER THEN Player B wins round

Etc…

The Mechanics of RSP are based on game agents looking for discernible patterns in their opponent’s behavior. For instance, if an opponent chooses rock and you choose rock, is there something about their behavior which suggests you might be able to predict the outcome of the next round based on the previous. I would say that this is not deep in comparison to other games, however the significant meta-game elements means that RSP is a little deep, but only when played face to face, with other humans.

Now, if we are to examine the mechanics, rules and systems of RSP we could express it like this... (Figure 1)

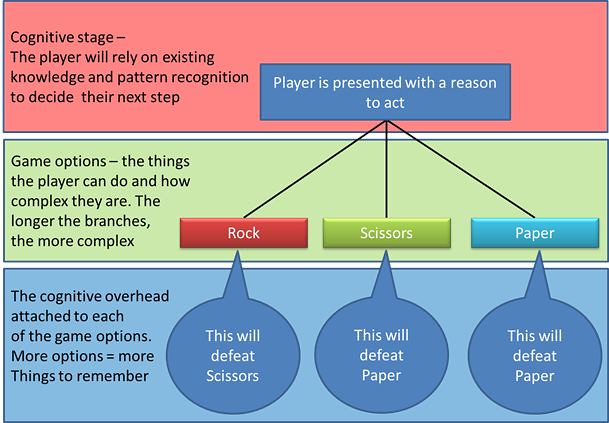
Figure 1

In the first (red stage) the player has something that they need to do. In the green. This is where the player can use mechanics. The outcome of the game is governed by rules and systems determine the winner. 

To help evaluate depth & complexity I fist like to map things out visually. My horizontal axis will usually give me an idea of complexity, whilst my vertical axis will generally give me an indication of depth. My visual mapping also only accounts for what I refer to as one round of the game. If a sentence in part of part of a larger narrative, then a 'round' is the individual sentences. You could also think of the concept of "outcomes" to limit your graphical mapping. How many actions are required before a game system will give a discernable outcome to the player. Now keep in mind that what a round is will always be dictated by the type of game that you are playing. Games may also seem to be deep if you haven't correctly brokem them down into individual components. This is a skill in iteelf, but not one I will delve into here. (Note that I do not consider the time it takes to reach an outcome a factor, just the amount of steps it takes to arrive at the outcome.[1])

If I am ever a little stuck with this processes, I will often ask myself if a certain 'round' requires strategy to complete, or just a single tactic. If I can complete a ‘round’ in a game just using a tactic, then I consider it to have little to no depth. If multiple different tactics are required (and hence form part of a strategy) to complete a ‘round’ of game then I consider it to have some depth. Lastly, if I can use a range of different strategies to achieve the same outcome or similar outcomes, then the game has significant depth. (but not necessarily complexity!) Complexity enters this equation when you consider what is required to achieve the tactic itself and how many tactics the game expects the player to know and use. 

So let’s analyze RSP using these questions;

Can I win a round of RSP just using tactics? (use this to begin to evaluate depth)

Yes, even if against a human player. (One round of RSP does not have depth)

How complex are the tactics to execute? (use this to understand complexity)

Not really difficult, I only have to do one of three things to execute a tactic. (RSP is of low complexity)

So, if we just look at one round of RSP and ignore the meta game that is often part of it, then we have a low complexity, low depth game. I would even go so far as to argue that ‘game’ is a strong word for the novice RSP player, but let’s not open that can of worms.

Low Complexity, Significant Depth

Now that we have some sort of taxonomy to differentiate the depth and complexity we need to understand the relative value of each. Does 1 Complexity = 1 Depth?

Every mechanic, rule and system will have a cognitive load associated with it. This is essentially the mental ‘cost’ associated with having to remember what certain game options do or more specifically in the context of mechanics, remembering how certain game actions alter the game systems in the players favor given the current state of said systems. In terms of cognitive load, both depth and complexity have a ‘cost’ but are they of equal cognitive value and is it better to load one up more than another?

In order to get more perspective on this problem, let’s consider two arcade titles; Radiant Silvergun , (Treasure, 1999) (Figure 2) & Ikaruga (Treasure, 2001). Both games are by the same developer and same designer and both share the same (or very similar) mechanics, rules & systems, they are fundamentally different, but without digging deeper it is hard to understand if this is a result from differences in complexity or depth or both.

Using the same approach used to map depth and complexity of RSP we can begin to unpack both titles. In both games, the player has one compulsory objective

And one additional, non-compulsory objective

For this analysis, I am going to consider that the player is aiming for the non-compulsory objective in addition to the compulsory objective.

Figure 2

Further to this, both games are a type of spatial puzzle, especially if the player is trying to achieve the non-compulsory objective. These spatial problems I consider to be the tangible embodiment of the games systems. The reason for this is that they represent consequence and force the player to adapt. The spatial puzzle systems can really only be measured in terms of their relative complexity. Increasing complexity forces the player to adopt strategy hence forcing the player to explore deeper mechanics to achieve the non-compulsory goal. Multiple tactics are needed as part of a larger strategy to clear the screen in a particular order. Complexity of the input scheme, couples with complexity of the systems mean that strategy is required.

Let’s adopt a system to quantify the complexity of these the spatial puzzles. I believe the most appropriate tool we have is the principle of minimum and maximum cutting derived from graph theory.

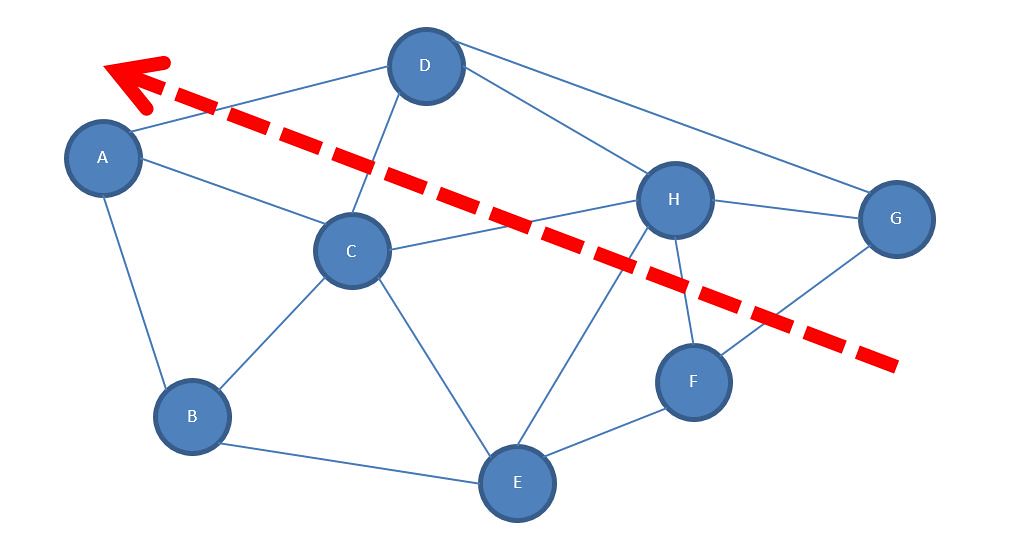
Figure 3

Imagine that in the graph depicted in Figure 3 that each node (labelled A through G) is an AI controlled enemy on screen. If the player simply wanted to strafe across the screen like the dotted red arrow depicts, then this would result in a minimum cut – i.e. taking the shortest possible route from one point to another. Often the decision to take a route will be based on the experience of the players. Novices under stress may choose the safest option, whilst experience players will usually find this the least appealing path. The designers of Radiant Silvergun have provided an alternative for experienced players wishing to achieve the non-compulsory objective. In all cases, the non-compulsory objective is enforced by forcing the player to undertake strategies involving Maximum Cutting.

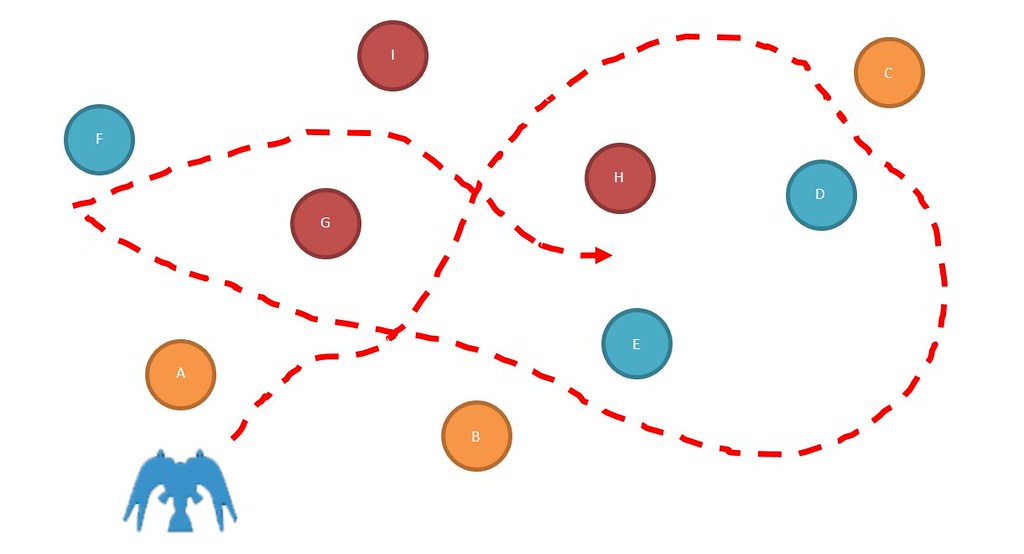
Figure 4

Figure 4 shows the principle of maximum cutting in relation to Radiant Silvergun. In this example, we can see that in order for the player to destroy enemies in groups of three, they will need to use a much more complex movement strategy in order to solve the spatial puzzle. Multiple tactics can be employed as part of a larger strategy forcing the game to be deep. But is it complex?

Radiant Silvergun and Ikaruga are fundamentally different to  RSP. In RSP, each game agent has the exact same options (mechanics) available to them. In Radiant Silvergun and Ikaruga the game agents have significant different options available to them (albeit completely scripted and predictable). Further to this, the AI agents in both games are non-adaptive. That is, although they do certain adaptive actions like aiming, all AI agents are consistent in their behaviors. This difference causes a tremendous cognitive cost for the player as they will need to remember far more information in order to be successful, however the cost is mitigated by having similar looking enemies behave in similar ways throughout the game.

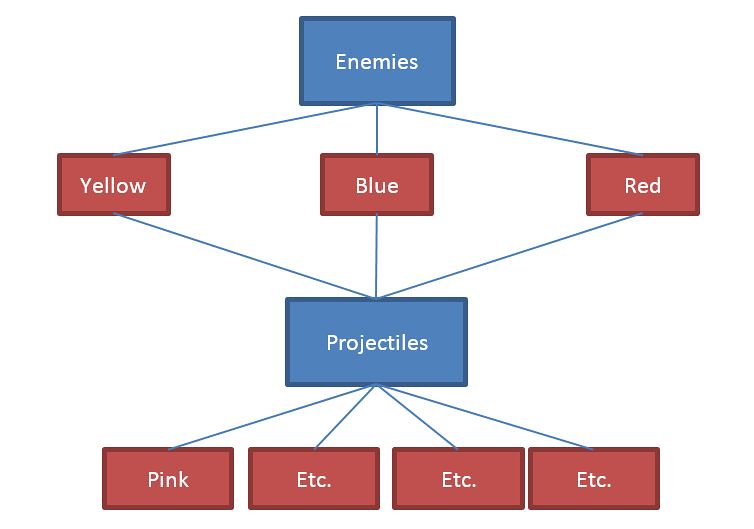
Figure 5

For every type of enemy in Radiant Silveregun, the player needs to remember what they do and how their actions impact on the game current state of the game systems. Figure 5 is one small part of the entire “tree” of information that the player needs to remember just for enemy information. In Radiant Silveregun there are multiple enemy agents. Each class of enemy agent can be one of three colors. Further to this, each enemy agent can usually fire multiple classes of projectiles. In other terms, the player is expected to learn and memorize multiple possible behaviors for agents that a represented in a similar way. This is somewhat complex due to the sheer amount of different enemies. It also has some minimal depth as the agents have some variation in their tactics – no enemies though have a strategy.

Things start to get even more complex when we consider the options that the player has and the cognitive load associated with this. Figure 6 is what the player can do in Radiant Silvergun. The breadth of these options suggests higher than normal complexity for an arcade game. (Note that the movement options and fire options should be at the same level of the hierarchy, however due to formatting constraints they have been represented one after the other.)

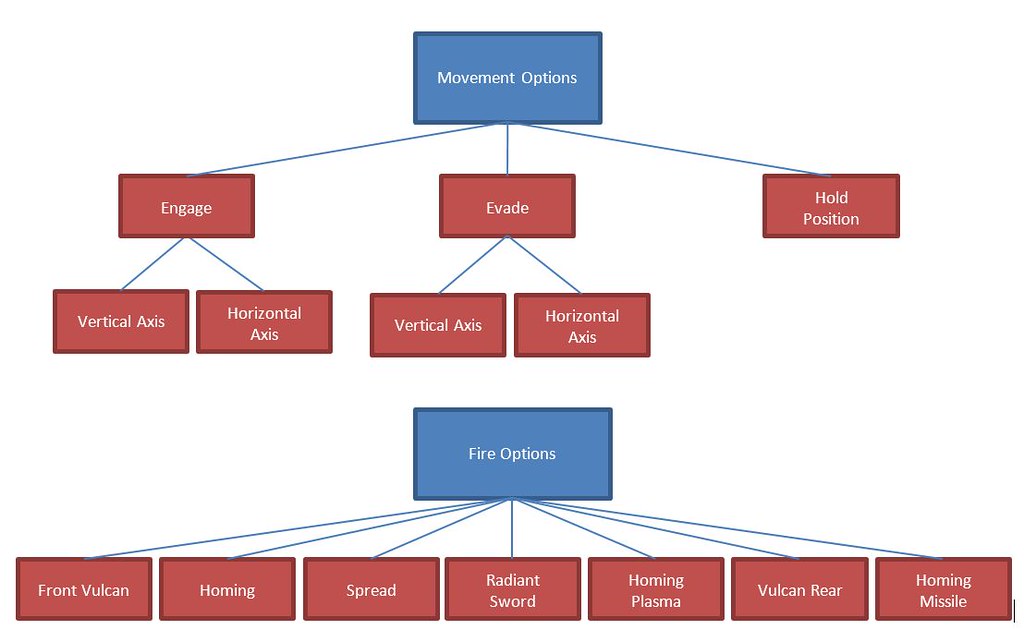
Figure 6

For each of the fire options, the player needs to remember what they do and how to trigger them. The possible interactions are therefore complex by virtue of their quantity;

Now these weapons are not just for aesthetic purposes, they are used to solve maximum cutting problems and clear a path for the player to move (and engage) along multiple vectors. (Figure 7) The combination of these two things cause the game to have the most depth when going for the non-compulsory object.

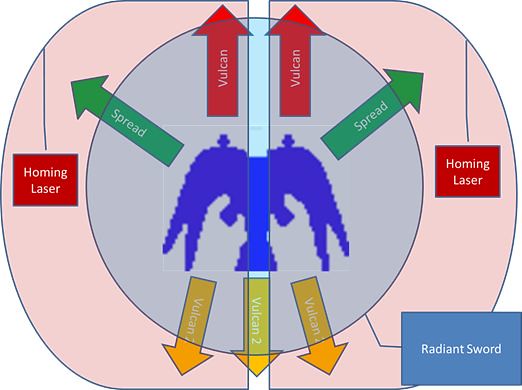
Figure 7

If we put the complexity of the players options together with the strategy forced by undertaking maximum cutting then we have game mechanics which are deep; (Figure 8)

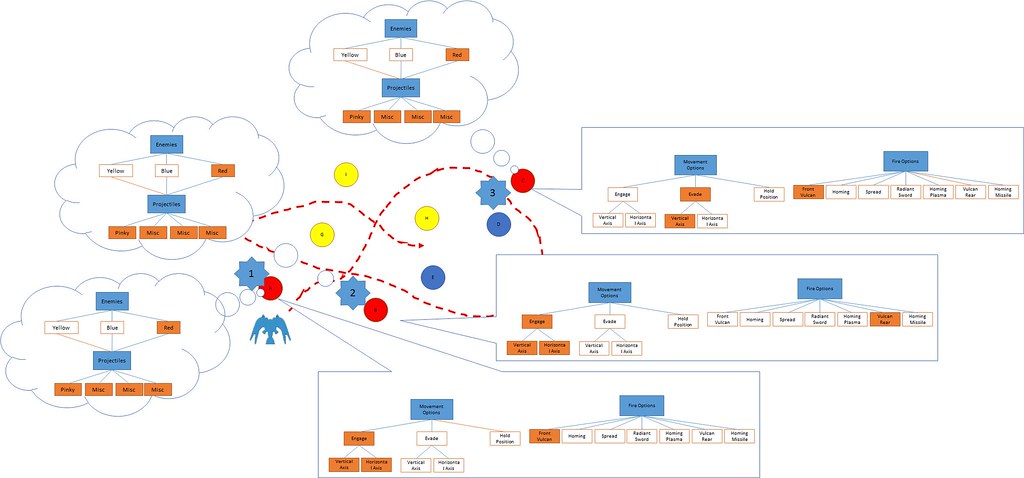
Figure 8 (click for large image)

At each one of the first three points in Figure 8, the player needs to evaluate their spatial position, evaluate the immediate threat, then decide what they are to do in order to address both main objectives of the game. Although there is an ideal maximum cutting route in this example, it could be solved using multiple different strategies.

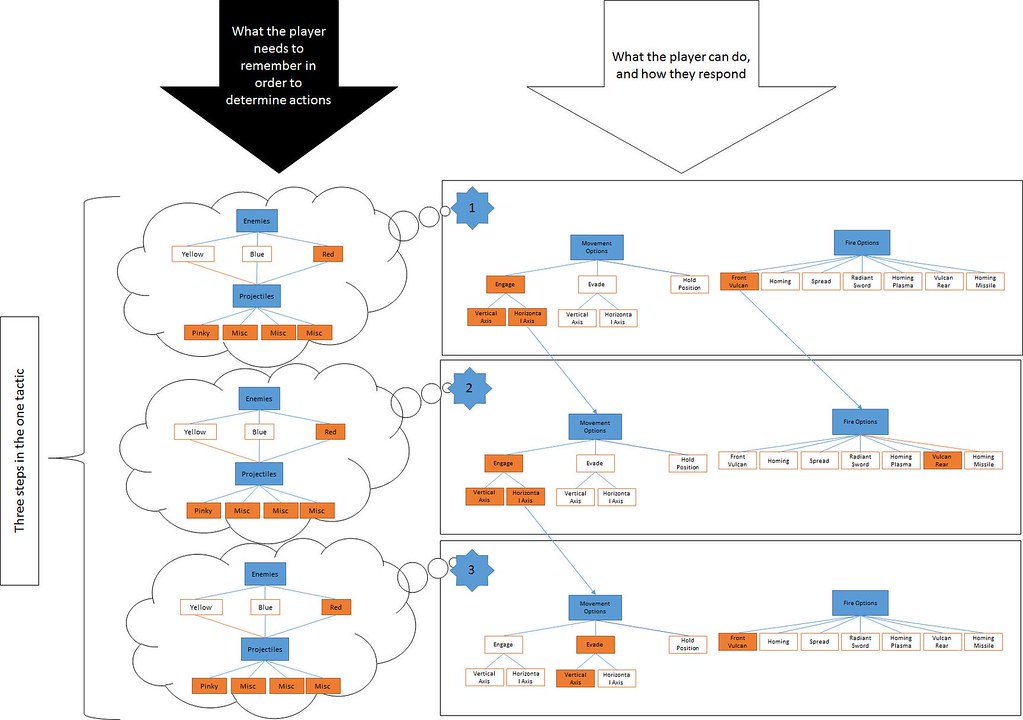
Figure 9 (click for large image)

If we represent these first three steps as a linear sequence (Figure 9) we can begin to see how deep the decision making process (depth) needs to be for effective strategy. We also get a clear indication of complexity as seen in the overall physical width of the options at each stage. Note that rule complexity is low as the the same rules are enforced at each layer of the decision making process.

To put this one diagram into context of the larger game experience, to reach a world record score in Radiant Silvergun you will be required to do this for minutes at a time, without a break, without failure! The issue is that Radiant Silvergun gives us a false sense of depth and complexity as the depth /strategy element can be learnt and refined. At the end of the day, this still means that we are really dealing with a game which is more complex, than it is deep.

Ikaruga

If we move beyond Radiant Silvergun to its spiritual successor, then we can see how even simple reductions in player options will result in a far more manageable levels of complexity.

Figure 10
 

Ikaruga (Figure 10) has the exact same objectives (both compulsory and noncompulsory) as Radiant Silvergun. Ikrauga also has the same spatial problem solving as Radiant Silvergun, relying on the player to use their weapons to solve the maximum cutting problems in each section of the game. Ikaruga though has lower complexity and as a result a reduction mechanical complexity and depth.

Instead of their being three colours of enemy, there is now only two and instead of having seven weapons, there is only two. Ironically, this reduction in mechanical and system complexity allows Ikaruga to be more complex in the maximum cutting problems and duration of encounters. The reason being that the lower complexity of spatial puzzles allows for more, different strategies to be applied to achieve the same goal. Think of it this way, if you have to drive from point A to point B then you will have multiple different routes and options available to you. If however, you needed to pickup a friend along the way, then this is going to begin to reduce the total amount of options you might take. The total possibilities are always tempered by the logistics of the constraints along the way.

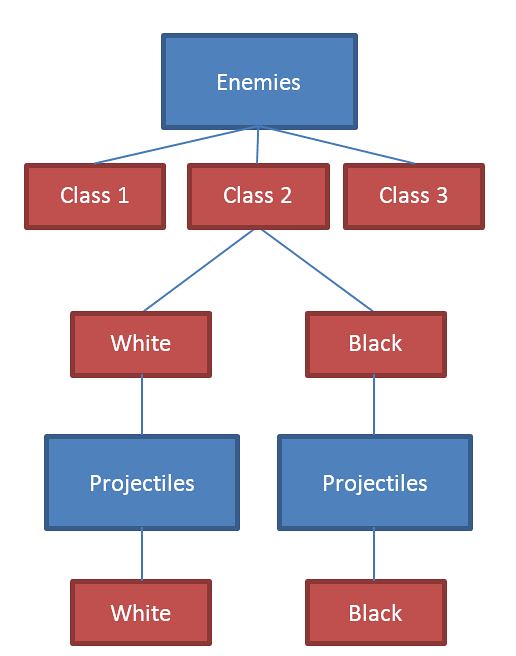
Figure 11

The reduction of complexity in Ikaruga is further demonstrated in a revision to design of its enemies. This can be seen in Figure 11. In Radiant Silvergun, each enemy could often shoot multiple different projectile types, however Ikaruga ‘nests’ the projectile type in in the enemy colour type. What this means is enemy tactics become one dimensional and hence have no depth . When the player looks at an enemy in Ikaruga, they can immediately predict (and pre-empt) the type of projectile that will come towards them and adjust accordingly. As a side note, projectiles in Ikaruga tend to have a slightly higher velocity than Radiant Silvergun. Ikaruga also ‘nests’ the fire type for the player, which greatly reduces the complexity of the input scheme. (Figure 12)

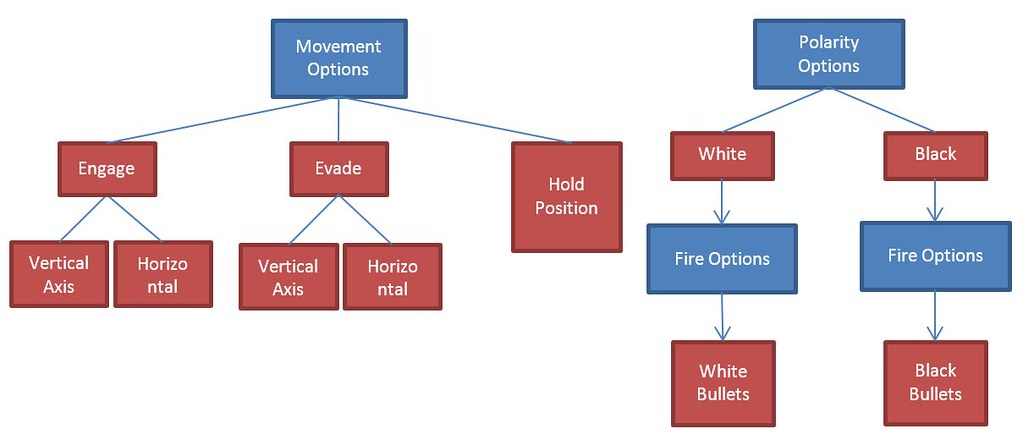
Figure 12

Due to the reduction in complexity, we also have a reduction in the cognitive load associated with remember and processing this complexity. This also highlights that complexity and depth are different types of cognitive skills. Is complexity more reliant on recall and memory and is depth more reliant onanalytical thinking? I think so, but unfortunately I’m not qualified to say that!

But what about the spatial design, does this have enough complexity to result in depth? Ikaruga may be less complex in some areas, however the addition of more rules results in a deeper set of mechanics. Ikaruga adds in an additional set of rules to promote deeper strategy in spatial problem solving. This is achieved introducing a set of rules allowing the player to absorb enemy bullets if their shields are the same colour as the enemies projectiles;

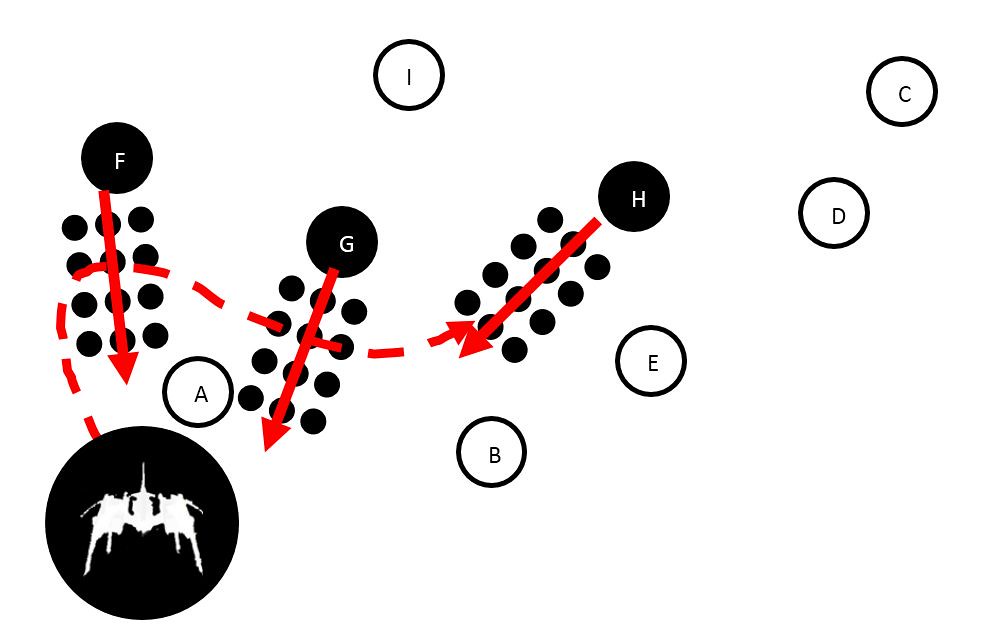
Figure 13

Figure 14

To demonstrate the differences between Ikaruga and Radiant Silvergun, Figure 13 & Figure 14 are used to represent two successive steps in the same scenario. In Figure 13, the player chooses the black shield (and by defacto, the black fire type) making them immune to the incoming barrage of black bullets. The player destroys this group of three black enemies resulting in a chain bonus. Once the black enemies are removed, the player can then use a maximum cutting solution to engage the remaining white enemies in Figure 14.

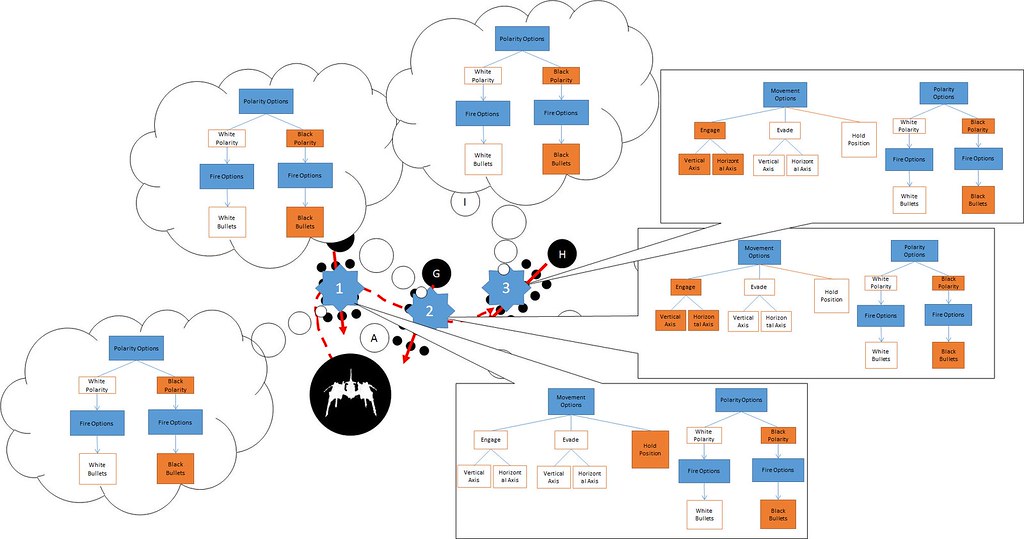
Figure 15 (click for large image)

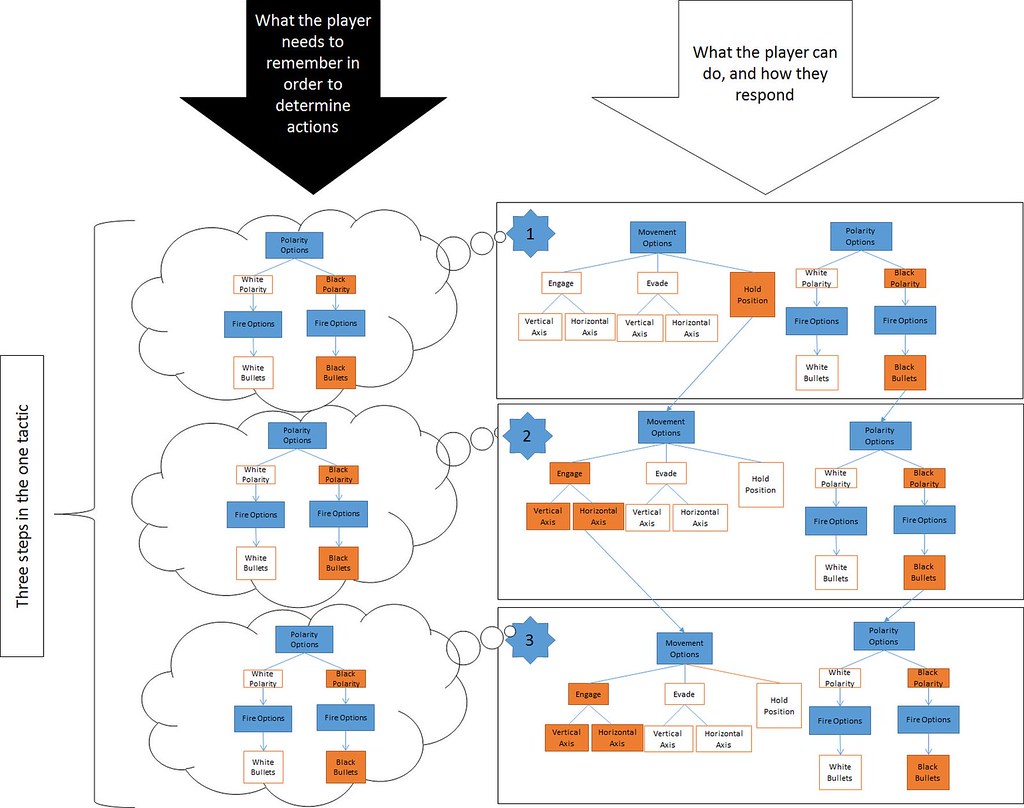
Figure 16 (click for large image)

Figure 15 & Figure 16 are breakdowns of the depth and complexity in Ikaruga using the same principle that was applied to the Radiant Silvergun example. As we can see, the reduction in complexity of options, such as the nesting of fire types and reduction in enemy classes and colours significantly reduces the complexity BUT it does allow for different strategies to be applied, hence resulting in greater depth (at least as an outcome of my methodology). This depth is evident in more complex and varied maximum cutting solution. By reducing options and enemy types the designers have cleverly reduced the amount of dominant strategies. This allows the game to have greater depth as each spatial puzzle will have multiple solutions, all of which yield a positive outcome in the immediate scenario BUT may have an impact in the transition between scenarios. (for example, completely a spatial puzzle and ending up in one section of the screen compared to another will have an impact of the tactics required to solve the next maximum cutting problem.

Conclusion & Lessons Learnt

Although I have really only looked at two genre-specific examples, I think that there is a lot to take away from depth and complexity analysis of the games we like. Here are some of the pointers for me. Some taken from this analysis, some taken from reflecting on my own gaming experiences;

The last and probably most important lesson learnt from this analysis can only be answered when coming back to pondering if Decathlete is a deep game? If we use the approach I used in this document then Decathlete is neither complex, nor is it deep. But you know what? I don’t care! I still had an absolute blast playing it today on a big, old blurry arcade cabinet with a bunch of other folks having fun, either playing or watching. So the final lesson learnt, and probably the most important;

Rock, Scissors, Paper anyone?

[1] Time is a metric of difficulty fine tuning. It works by disconnecting cause and response associations in the mind of the player, taking more attention to identify exploitable patterns.