Trending
Opinion: How will Project 2025 impact game developers?
The Heritage Foundation's manifesto for the possible next administration could do great harm to many, including large portions of the game development community.
The idea of using the stencil buffer to generate shadows has been around for over a decade, but only recently has 3D graphics hardware advanced to the point where using the stencil algorithm on a large scale has become practical. Not long ago, there existed some unsolved problems pertaining to stencil shadows that prevented the algorithm from working correctly under various conditions. Advances have now been made, however, so that stencil shadows can be robustly implemented to handle arbitrarily positioned point lights and infinite directional lights having any desired spatial relationship with the camera. This article presents the intricacies of the entire stencil shadow algorithm and covers every mathematical detail of its efficient implementation.

The idea of using the stencil buffer to generate shadows has been around for over a decade, but only recently has 3D graphics hardware advanced to the point where using the stencil algorithm on a large scale has become practical. Not long ago, there existed some unsolved problems pertaining to stencil shadows that prevented the algorithm from working correctly under various conditions. Advances have now been made, however, so that stencil shadows can be robustly implemented to handle arbitrarily positioned point lights and infinite directional lights having any desired spatial relationship with the camera. This article presents the intricacies of the entire stencil shadow algorithm and covers every mathematical detail of its efficient implementation.
The basic concept of the stencil shadow algorithm is to use the stencil buffer as a masking mechanism to prevent pixels in shadow from being drawn during the rendering pass for a particular light source. This is accomplished by rendering an invisible shadow volume for each shadow-casting object in a scene using stencil operations that leave nonzero values in the stencil buffer wherever light is blocked. Once the stencil buffer has been filled with the appropriate mask, a lighting pass only illuminates pixels where the value in the stencil buffer is zero.
As shown in Figure 1, an object’s shadow volume encloses the region of space for which light is blocked by the object. This volume is constructed by finding the edges in the object’s triangle mesh representing the boundary between lit triangles and unlit triangles and extruding those edges away from the light source. Such a collection of edges is called the object’s silhouette with respect to the light source. The shadow volume is rendered into the stencil buffer using operations that modify the stencil value at each pixel depending on whether the depth test passes or fails. Of course, this requires that the depth buffer has already been initialized to the correct values by a previous rendering pass. Thus, the scene is first rendered using a shader that applies surface attributes that do not depend on any light source, such as ambient illumination, emission, and environment mapping.
Figure 1. An object’s shadow volume encloses the region of space for which light is blocked by the object. |
The original stencil algorithm renders the shadow volume in two stages. In the first stage, the front faces of the shadow volume (with respect to the camera) are rendered using a stencil operation that increments the value in the stencil buffer whenever the depth test passes. In the second stage, the back faces of the shadow volume are rendered using a stencil operation that decrements the value in the stencil buffer whenever the depth test passes. As illustrated in Figure 2, this technique leaves nonzero values in the stencil buffer wherever the shadow volume intersects any surface in the scene, including the surface of the object casting the shadow.
Figure 2. Numbers at the ends of rays emanating from the camera position C represent the values left in the stencil buffer for a variety of cases. The stencil value is incremented when front faces of the shadow volume pass the depth test, and the stencil value is decremented when back faces of the shadow volume pass the depth test. The stencil value does not change when the depth test fails. |
There are two major problems with the method just described. The first is that no matter what finite distance we extrude an object’s silhouette away from a light source, it is still possible that it is not far enough to cast a shadow on every object in the scene that should intersect the shadow volume. The example shown in Figure 3 demonstrates how this problem arises when a light source is very close to a shadow-casting object. Fortunately, this problem can be elegantly solved by using a special projection matrix and extruding shadow volumes all the way to infinity.
Figure 3. No matter what finite distance an object’s silhouette is extruded away from a light source, moving the light close enough to the object can result in a shadow volume that cannot reach other objects in the scene. |
The second problem shows up when the camera lies inside the shadow volume or the shadow volume is clipped by the near plane. Either of these occurrences can leave incorrect values in the stencil buffer causing the wrong surfaces to be illuminated. The solution to this problem is to add caps to the shadow volume geometry, making it a closed surface, and using different stencil operations. The two caps added to the shadow volume are derived from the object’s triangle mesh as follows. A front cap is constructed using the unmodified vertices of triangles facing toward the light source. A back cap is constructed by projecting the vertices of triangles facing away from the light source to infinity. For the resulting closed shadow volume, we render back faces (with respect to the camera) using a stencil operation that increments the stencil value whenever the depth test fails, and we render front faces using a stencil operation that decrements the stencil value whenever the depth test fails. As shown in Figure 4, this technique leaves nonzero values in the stencil buffer for any surface intersecting the shadow volume for arbitrary camera positions. Rendering shadow volumes in this manner is more expensive than using the original technique, but we can determine when it’s safe to use the less-costly depth-pass method without having to worry about capping our shadow volumes.
Figure 4. Using a capped shadow volume and depth-fail stencil operations allows the camera to be inside the shadow volume. The stencil value is incremented when back faces of the shadow volume fail the depth test, and the stencil value is decremented when front faces of the shadow volume fail the depth test. The stencil value does not change when the depth test passes. |
The details of everything just described are discussed throughout the remainder of this article. In summary, the rendering algorithm for a single frame runs through the following steps.
A Clear the frame buffer and perform an ambient rendering pass. Render the visible scene using any surface shading attribute that does not depend on any particular light source.
B Choose a light source and determine what objects may cast shadows into the visible region of the world. If this is not the first light to be rendered, clear the stencil buffer.
C For each object, calculate the silhouette representing the boundary between triangles facing toward the light source and triangles facing away from the light source. Construct a shadow volume by extruding the silhouette away from the light source.
D Render the shadow volume using specific stencil operations that leave nonzero values in the stencil buffer where surfaces are in shadow.
E Perform a lighting pass using the stencil test to mask areas that are not illuminated by the light source.
F Repeat steps B through E for every light source that may illuminate the visible region of the world.
For a scene illuminated by n lights, this algorithm requires at least n+1 rendering passes. More than n+1 passes may be necessary if surface shading calculations for a single light source cannot be accomplished in a single pass. To efficiently render a large scene containing many lights, one must be careful during each pass to render only objects that could potentially be illuminated by a particular light source. An additional optimization using the scissor rectangle can also save a significant amount of rasterization work -- this optimization is discussed in the last section of this article.
To ensure that shadow volumes surround every last bit of space for which light is blocked by an object, we must extrude the object’s silhouette to infinity. Using a standard perspective projection matrix would cause such a shadow volume to be clipped by the far plane. To avoid this unwanted effect, we can actually place the far plane at an infinite distance from the camera.
Recall that the projection matrix transforms points from eye space to clip space. In OpenGL, eye space is the coordinate system in which the camera lies at the origin, the x-axis points to the right, the y-axis points upward, and the camera points down the negative z-axis. In clip space, a 4D homogeneous point <x,y,z,w> is inside the view frustum if -w<x<w, -w<y<w, and -w<z<w. Once primitives have been clipped, a vertex is transformed into a 3D point in normalized device coordinates by performing a perspective divide by its w-coordinate. This results in a point whose x, y, and z coordinates all lie in the range [-1,1]. In the final transformation before rasterization, these coordinates are remapped to the dimensions of the viewport and the physical range of the depth buffer.
The standard OpenGL perspective projection matrix P has the form
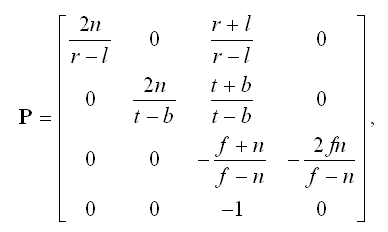 (1)
(1)
where n is the distance to the near plane, f is the distance to the far plane, and l, r, b, and t represent the left, right, bottom, and top edges of the rectangle carved out of the near plane by the view frustum. By evaluating the limit as f tends to infinity, we obtain the matrix
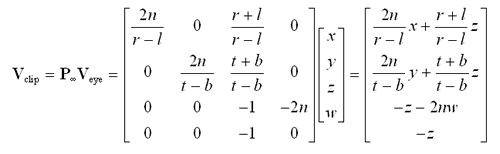 (2)
(2)
The matrix P¥ transforms a 4D homogeneous eye-space point Veye=<x,y,z,w> to the clip-space point Vclip as follows.
 (3)
(3)
Assuming w>0 (it is normally the case that w=1), the resulting z-coordinate of is always less than the resulting w-coordinate of Vclip, ensuring that projected points are never clipped by the far plane. A point at infinity is represented by 4D homogeneous vector having a w-coordinate of zero in eye space. For such a point, (Vclip)z = (Vclip)w, and the perspective divide produces a 3D point in normalized device coordinates having the maximal z-value of one.
In practice, the limitations of hardware precision can produce points having a normalized z-coordinate slightly greater than one. This causes severe problems when the z-coordinate is converted to an integer value to be used in the depth buffer because the stencil operations that depend on the depth test to render shadow volumes may no longer function correctly. To circumvent this undesirable effect, we can map the z-coordinate of a point at infinity to a value slightly less than one in normalized device coordinates. The z-coordinate of a 3D point D in normalized device coordinates is mapped from a value Dz in the range [-1,1] to a value D'z in the range [-1,1-e], where e is a small positive constant, using the relation
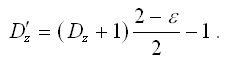 (4)
(4)
We need to find a way to modify the z-coordinate of Vclip in order to perform this mapping as points are transformed from eye space into clip space. We can rewrite Equation (4) as an adjustment to (Vclip)z by replacing Dz with (Vclip)z / (Vclip)w and D'z with (V'clip)z / (Vclip)w as follows.
 (5)
(5)
Plugging in the values of and given by equation (3), we have
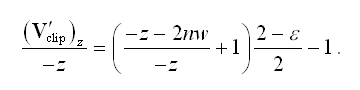 (6)
(6)
Solving for and simplifying yields
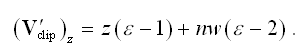 (7)
(7)
We can incorporate this mapping into the projection matrix P¥ given by Equation (2) as follows to arrive at the slightly tweaked matrix P'¥ that we actually use to render a scene.
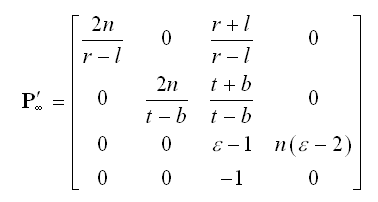 (8)
(8)
If the graphics hardware supports depth clamping, then use of the matrix P'¥ given by Equation (8) is not necessary. The GL_NV_depth_clamp extension to OpenGL allows a renderer to force depth values in normalized device coordinates to saturate to the range [-1,1], thus curing the precision problem at the infinite far plane. When depth clamping is enabled using the function call
glEnable(GL_DEPTH_CLAMP_NV);
the projection matrix P¥ given by Equation (2) can safely be used.
The question of depth buffer precision arises when using an infinite projection matrix. It is true that placing the far plane at infinity reduces the number of discrete depth values that can occur within any finite interval along the z-axis, but in most situations this effect is small. Consider the function that uses the matrix P given in Equation (1) to map an eye-space point V=<Vx,Vy,Vz,1> to its corresponding depth in normalized device coordinates:
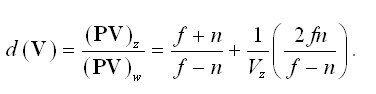 (9)
(9)
We obtain a different dfunction d¥(V) by using the matrix P¥ given by Equation (2) to map an eye-space point V to its normalized depth:
 (10)
(10)
Given two eye-space points V1and V2, we can compare the differences in depth values produced by the functions d and d¥ as follows.
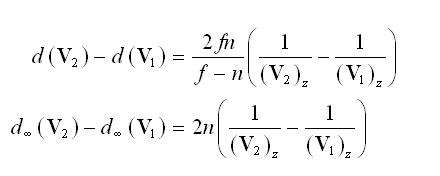 (11)
(11)
This demonstrates that the standard projection matrix P maps the points V1and V2 to a range that is a factor f /(f-n) larger than the range to which the points are mapped by the infinite projection matrix , thus equating to greater precision. For practical values of f and n, where f is much larger than one and n is much smaller than one, is close to unity, so the loss of precision is not a significant disadvantage.
The stencil shadow algorithm requires that the models in our world be closed triangle meshes. In mathematical terms, the surface of any object that casts a shadow must be a two-dimensional closed manifold. What this boils down to is that every edge in a mesh must be shared by exactly two triangles, disallowing any holes that would let us see the interior of the mesh.
Edge connectivity information must be precomputed so that we can determine a mesh’s silhouette for shadow volume rendering. Suppose that we have an indexed triangle mesh consisting of an array of N vertices V1,V2,…,VN and an array of M triangles T1,T2,…,TM. Each triangle simply indicates which three vertices it uses by storing three integer indexes i1, i2, and i3. We say that an index ip precedes an index iq if the number p immediately precedes the number q in the cyclic chain 1®2®3®1. For instance, i2 precedes i3 and i3 precedes i1, but i2 does not precede i1.
The indexes i1, i2, and i3 are ordered such that the positions of the vertices Vi1, Vi2, and Vi3 to which they refer are wound counterclockwise about the triangle’s normal vector. Suppose that two triangles share an edge whose endpoints are the vertices Va and Vb as shown in Figure 5. The consistent winding rule enforces the property that for one of the triangles, the index referring to Va precedes the index referring to Vb, and that for the other triangle, the index referring to Vb precedes the index referring to Va.
Figure 5. When consistent winding is enforced, it is always the case that the indexes referring to the vertices Va and Vb of exactly one of the two triangles sharing an edge satisfies the property that the index referring to Va precedes the index referring to Vb. |
As demonstrated in Listing 1, the edges of a triangle mesh can be identified by making a single pass through the triangle list. For any triangle having vertex indexes i1, i2, and i3, we create an edge record for every instance in which i1< i2, i2< i3, or i3< i1and store the index of the current triangle in the edge record. This procedure creates exactly one edge for every pair of triangles that share two vertices Va and Vb, duplicating any edges that are shared by multiple pairs of triangles.
Once we have identified all the edges, we make a second pass through the triangle list to find the second triangle that shares each edge. This is done by locating triangles for which i1> i2, i2> i3, or i3> i1 and matching it to an edge having the same vertex indexes that has not yet been supplied with a second triangle index.
Armed with the edge list for a triangle mesh, we determine the silhou¹ette by first calculating the dot product between the light position and the plane of each triangle. For a triangle whose vertex indexes are i1, i2, and i3, the (unnormalized) outward-pointing normal direction N is given by
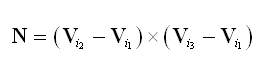 (12)
(12)
since the vertices are assumed to be wound counterclockwise. The 4D plane vector K corresponding to the triangle is then given by
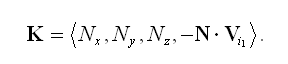 (13)
(13)
Let L represent the 4D homogeneous position of the light source. For point light sources, LW≠0, and for infinite directional light sources, LW=0. A triangle faces the light source if K·L>0; otherwise, the triangle faces away from the light source. The silhouette is equal to the set of edges shared by one triangle facing the light and one triangle facing away from the light.
Once the set of an object’s silhouette edges has been determined with respect to a light source, we must extrude each edge away from the light’s position to form the object’s shadow volume. In this section, we present methods that perform the extrusion by making use of widely available vertex programming hardware exposed by the GL_NV_vertex_program and GL_EXT_vertex_shader extensions to OpenGL.
For a point light source, the extrusion of the silhouette edges consists of a set of quads, each of which has the two unmodified vertices belonging to an edge and two additional vertices corresponding to the extrusion of the same edge to infinity. For an infinite directional light source, all points project to the same point at infinity, so the extrusion of the silhouette edges can be represented by a set of triangles that all share a common vertex. We distinguish between points that should be treated normally and those that should be extruded to infinity by using 4D homogeneous coordinates. A w-coordinate of one is assigned to the unmodified vertices and a w-coordinate of zero is assigned to the extruded vertices. The extrusion methods that we present utilize the information stored in the w-coordinate to perform the appropriate vertex modifications.
Before we examine the extrusion methods, we must prepare the appropriate quad list or triangle list (depending on whether we are using a point light or infinite directional light). We need to make sure that the vertices of each extrusion primitive are wound so that the face’s normal direction points out of the shadow volume. Suppose that a silhouette edge E has endpoints A and B. The edge-finding code presented in Listing 1 associates the triangle for which the vertices A and B occur in counterclockwise order as the first triangle sharing the edge E. Thus, if the first triangle faces toward the light source, then we want the vertices A and B to occur in the opposite order for the extruded primitive so that its vertices are wound counterclockwise. If the first triangle faces away from the light source, then we use the vertices A and B in the same order for the extruded primitive. Table 1 lists the vertices of the extrusion of the edge E for point light sources and infinite directional light sources for the cases that the first triangle associated with the edge E faces toward or away from the light source.
Table 1. Given a silhouette edge E having endpoints A and B, this table lists the object-space vertices of the extruded shadow volume face corresponding to E. The first triangle associated with the edge E is the triangle for which the vertices A and B occur in counterclockwise order.

Using the GL_NV_vertex_program extension, we can employ a couple simple vertex programs to perform edge extrusion and transformation to clip space. In each program, we assume that the product of the projection matrix and model-view matrix has been tracked into constant registers c[0]–c[3] and that the object-space light position has been stored in constant register c[4]. Vertex programs are enabled and these constants are loaded using the following function calls, where lx, ly, lz, and lw represent the light position.
glEnable(GL_VERTEX_PROGRAM_NV);
glTrackMatrixNV(GL_VERTEX_PROGRAM_NV, 0,
GL_MODELVIEW_PROJECTION_NV, GL_IDENTITY_NV);
glProgramParameter4fNV(GL_VERTEX_PROGRAM_NV, 4, lx, ly, lz, lw);
For a point light source residing at the point L in object space, a vertex V from Table 1 is unmodified if its w-coordinate is one and is extruded if its w-coordinate is zero by using the formula
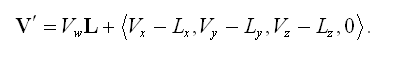 (14)
(14)
The following vertex program applies this formula and then transforms the resulting vertex position into clip space.
!!VP1.0
ADD R0.xyz, v[OPOS], -c[4];
MAD R0, v[OPOS].w, c[4], R0;
DP4 o[HPOS].x, c[0], R0;
DP4 o[HPOS].y, c[1], R0;
DP4 o[HPOS].z, c[2], R0;
DP4 o[HPOS].w, c[3], R0;
END
In the case that shadow volume caps must be rendered (see the next section), a vertex program nearly identical to the one above should be used to transform vertices belonging to triangles that face away from the light source. Such vertices can be treated as if their w-coordinates are zero, so the MAD instruction has no effect and can be removed when projecting a back cap.
For an infinite light source residing at the point L (having w-coordinate zero) in object space, a vertex V is unmodified or extruded by using the formula
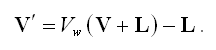 (15)
(15)
The following vertex program applies this formula and then transforms the resulting vertex position V' into clip space.
!!VP1.0
ADD R0, v[OPOS], c[4];
MAD R0, v[OPOS].w, R0, -c[4];
DP4 o[HPOS].x, c[0], R0;
DP4 o[HPOS].y, c[1], R0;
DP4 o[HPOS].z, c[2], R0;
DP4 o[HPOS].w, c[3], R0;
END
The formulas given by Equations (14) and (15) can also be implemented using the GL_EXT_vertex_shader extension. Within our vertex shaders, we need to track model-view-projection matrix and the current vertex position, and we need to define an invariant corresponding to the object-space light position. Vertex shaders are enabled and these values are initialized using the following code, where lpos points to the first component of the light position.
glEnable(GL_VERTEX_SHADER_EXT);
GLuint mvp_matrix = glBindParameterEXT(GL_MVP_MATRIX_EXT);
GLuint vertex_pos = glBindParameterEXT(GL_CURRENT_VERTEX_EXT);
GLuint light_pos = glGenSymbolsEXT(GL_VECTOR_EXT,
GL_INVARIANT_EXT, GL_FULL_RANGE_EXT, 1);
glSetInvariantEXT(light_pos, GL_FLOAT, &lpos);
For a point light source, Equation (14) can be implemented using the following vertex shader code, which also performs the transformation into clip space. We define a few temporary variables to hold intermediate results.
glBeginVertexShaderEXT();
GLuint temp1 = glGenSymbolsEXT(GL_VECTOR_EXT,
GL_LOCAL_EXT, GL_FULL_RANGE_EXT, 1);
GLuint temp2 = glGenSymbolsEXT(GL_SCALAR_EXT,
GL_LOCAL_EXT, GL_FULL_RANGE_EXT, 1);
GLuint swiz = glGenSymbolsEXT(GL_VECTOR_EXT,
GL_LOCAL_EXT, GL_FULL_RANGE_EXT, 1);
glShaderOp2EXT(GL_OP_SUB_EXT, temp1, vertex_pos, light_pos);
glExtractComponentEXT(temp2, vertex_pos, 3);
glSwizzleEXT(swiz, temp1, GL_X_EXT, GL_Y_EXT,
GL_Z_EXT, GL_ZERO_EXT);
glShaderOp3EXT(GL_OP_MADD_EXT, temp1, temp2, light_pos, swiz);
glShaderOp2EXT(GL_OP_MULTIPLY_MATRIX_EXT,
GL_OUTPUT_VERTEX_EXT, mvp_matrix, temp1);
glEndVertexShaderEXT();
For an infinite light source, we can replace the operations performed in the point light case with the following code to implement Equation (15).
glShaderOp2EXT(GL_OP_ADD_EXT, temp1, vertex_pos, light_pos);
glExtractComponentEXT(temp2, vertex_pos, 3);
glSwizzleEXT(swiz, temp1, GL_NEGATIVE_X_EXT,
GL_NEGATIVE_Y_EXT, GL_NEGATIVE_Z_EXT, GL_NEGATIVE_W_EXT);
glShaderOp3EXT(GL_OP_MADD_EXT, temp1, temp2, temp1, swiz);
glShaderOp2EXT(GL_OP_MULTIPLY_MATRIX_EXT,
GL_OUTPUT_VERTEX_EXT, mvp_matrix, temp1);
Determining Whether Caps are Necessary
As mentioned earlier, a completely closed shadow volume having a front cap and a back cap must be rendered whenever the camera lies inside the shadow volume or the faces of the silhouette extrusion could potentially be clipped by the near plane. We wish to render this more expensive shadow volume as infrequently as possible, so a test for determining when it is not necessary would be useful.
The near rectangle is the rectangle carved out of the near plane by the four side planes of the view frustum. As shown in Figure 6, we can devise a test to determine whether the shadow volume might be clipped by the near plane by constructing the set of planes that connect the boundary of the near rectangle to the light source. We call the volume of space bounded by these planes and by the near plane itself the near-clip volume. Only a point inside the near-clip volume can have an extrusion away from the light source that intersects the near rectangle. Thus, if an object is known to lie completely outside the near-clip volume, then we do not have to render a capped shadow volume.
Figure 6. The near-clip volume is bounded by the planes connecting the near rectangle to the light position L. If an object lies completely outside the near-clip volume, then it’s shadow volume cannot intersect the near rectangle, so it is safe to render it without caps.
When constructing the near-clip volume, we consider three cases: 1) the light source lies in front of the near plane, 2) the light source lies behind the near plane, and 3) the light source is very close to lying in the near plane. Let W be the transformation matrix that maps eye space to world space, and suppose that our light source lies at the 4D homogeneous point L in world space. We consider a point light source (for which LW=1) to be lying in the near plane if its distance to the near plane is at most some small positive value d. For an infinite directional light source (for which LW=0), we consider the distance to the near plane to be the length of the projection of the light’s normalized direction vector <Lx,Ly,Lz> onto the near plane’s normal direction. In either case, we can obtain a signed distance d from the light source to the near plane by calculating
(17)
If d>d, then the light source lies in front of the near plane; if d<-d, then the light source lies behind the near plane; otherwise, the light source lies in the near plane.
In the case that the light source lies in the near plane, the near-clip volume is defined by the planes K0=<0,0,-1,-n> and K1=<0,0,1,n>. These two planes are coincident, but have opposite normal directions. This encloses a degenerate near-clip volume, so testing whether an object is outside the volume amounts to determining whether the object intersects the near plane.
If the light source does not lie in the near plane, we need to calculate the vertices of the near rectangle. In eye space, the points R0, R1, R2, and R3 at the four corners of the near rectangle are given by
(18)
where n is the distance from the camera to the near plane, a is the aspect ratio of the viewport, equal to its height divided by its width, and e is the camera’s focal length, related to the horizontal field-of-view angle a by the equation e=1/tan (a/2). These four points are ordered counterclockwise from the camera’s perspective. For a light source lying in front of the near plane, the world-space normal directions Ni, where 0<i<3, are given by the cross products
(19)
where each R'i is the world-space vertex of the near rectangle given by R'i=WRi. For a light source lying behind the near plane, the normal directions are simply the negation of those given by Equation (19). The corresponding world-space planes Ki bounding the near-clip volume are given by
(20)
We close the near-clip volume by adding a fifth plane that is coincident with the near plane and has a normal pointing toward the light source. For a light source lying in front on the near plane, the fifth plane K4 is given by
(21)
and for a light source lying behind the near plane, the fifth plane is given by the negation of this vector. (Remember that if W is orthogonal, then (W-1)t =W.)
We determine whether a shadow-casting object lies completely outside the near-clip volume by testing the object’s bounding volume against each of the planes Ki. If the bounding volume lies completely on the negative side of any one plane, then the object’s shadow volume cannot intersect the near rectangle. In the case that an object is bounded by a sphere having center C and radius r, we do not need to render a capped shadow volume if Ki·C<-r for any i.
Figure 7 demonstrates that for point light sources, bounding volumes lying behind the light source from the camera’s perspective may often be mistaken for those belonging to objects that might cast shadows through the near rectangle. This happens when the bounding volume lies outside the near-clip volume, but does not fall completely on the negative side of any one plane. We can improve this situation substantially by adding an extra plane to the near-clip volume for point lights. As shown in Figure 7, the extra plane contains the light position L and has a normal direction that points toward the center of the near rectangle. The normal direction N5 is given by
(22)
and the corresponding plane K5 is given by
(23)
The plane K5 is added to the near-clip volume boundary for point light sources regardless of whether the light position is in front of, behind, or in the near plane.
Figure 7. Adding an extra plane to the near-clip volume for point light sources enables more objects to be classified as outside the near-clip volume.
See “For Further Information” at the end of this article for methods that can be used to determine whether other types of bounding volumes, such as ellipsoids, cylinders, and boxes, intersect the near-clip volume.
Rendering Shadow Volumes
Now that we can determine an object’s silhouette with respect to a light source, construct a shadow volume by extruding the silhouette edges away from the light source, and decide whether front and back caps are necessary, we are finally ready to render the shadow volume into the stencil buffer. We assume that the frame buffer has already been cleared and that an ambient rendering pass has been performed to initialize the depth buffer. This section concentrates on the operations necessary to illuminate the scene using a single light source, and these operations should be repeated for all light sources that can affect the visible region of the world being rendered.
First, we must clear the stencil buffer, configure the stencil test so that it always passes, and configure the depth test so that it passes only when fragment depth values are less than those already in the depth buffer. This is done using the following function calls.
glClear(GL_STENCIL_BUFFER_BIT);
glEnable(GL_STENCIL_TEST);
glStencilFunc(GL_ALWAYS, 0, ~0);
glEnable(GL_DEPTH_TEST);
glDepthFunc(GL_LESS);We are only going to be drawing into the stencil buffer, so we need to disable writes to the color buffer and depth buffer as follows.
glColorMask(GL_FALSE, GL_FALSE, GL_FALSE, GL_FALSE);
glDepthMask(GL_FALSE);Shadow volume faces are rendered using different stencil operations depending on whether they face toward or away from the camera, so we need to enable face culling with the following function call.
glEnable(GL_CULL_FACE);
For a shadow volume that does not require capping because it cannot possibly intersect the near rectangle, we modify the values in the stencil buffer when the depth test passes. The stencil value is incremented for fragments belonging to front-facing polygons and is decremented for fragments belonging to back-facing polygons. These operations are performed by the following function calls, where the function DrawShadowVolume() renders all of the polygons belonging to the shadow volume.
glCullFace(GL_BACK);
glStencilOp(GL_KEEP, GL_KEEP, GL_INCR);
DrawShadowVolume();glCullFace(GL_FRONT);
glStencilOp(GL_KEEP, GL_KEEP, GL_DECR);
DrawShadowVolume();If a shadow volume does require capping, then we modify the values in the stencil buffer when the depth test fails. The stencil value is incremented for fragments belonging to back-facing polygons and is decremented for fragments belonging to front-facing polygons (the opposite of the depth-pass operations). These operations are accomplished using the following function calls. In this case, the DrawShadowVolume() function renders the polygons belonging to the shadow volume’s caps as well as its extruded silhouette edges.
glCullFace(GL_FRONT);
glStencilOp(GL_KEEP, GL_INCR, GL_KEEP);
DrawShadowVolume();glCullFace(GL_BACK);
glStencilOp(GL_KEEP, GL_DECR, GL_KEEP);
DrawShadowVolume();Once shadow volumes have been rendered for all objects that could potentially cast shadows into the visible region of the world, we perform a lighting pass that illuminates surfaces wherever the stencil value remains zero. We re-enable writes to the color buffer, change the depth test to pass only when fragment depth values are equal to those in the depth buffer, and configure the stencil test to pass only when the value in the stencil buffer is zero using the following function calls.
glColorMask(GL_TRUE, GL_TRUE, GL_TRUE, GL_TRUE);
glDepthFunc(GL_EQUAL);
glStencilFunc(GL_EQUAL, 0, ~0);
glStencilOp(GL_KEEP, GL_KEEP, GL_KEEP);Since the lighting pass adds to the ambient illumination already present in the color buffer, we need to configure the blending equation as follows.
glEnable(GL_BLEND);
glBlendFunc(GL_ONE, GL_ONE);We also need to make the function call glCullFace(GL_BACK) just in case a depth-pass shadow volume was most recently rendered, leaving the culling state set to GL_FRONT. After the lighting pass has been rendered, we clean up by resetting a few rendering states back to those needed by the ambient pass for the next frame using the following function calls.
glDepthMask(GL_TRUE);
glDepthFunc(GL_LEQUAL);
glStencilFunc(GL_ALWAYS, 0, ~0);Because we needed to perform different stencil operations for front-facing polygons and back-facing polygons in our shadow volumes, we had to render the shadow volumes twice. Of course, the graphics hardware culled each polygon on either the first pass or the second, but the vertices still had to be processed two times. The GL_EXT_stencil_two_side extension to OpenGL provides a way to avoid this suboptimal situation by allowing separate stencil state for front faces and back faces to be specified simultaneously. When using this extension, we render both front faces and back faces of the shadow volume at the same time, so face culling should be disabled. We therefore prepare to render shadow volumes by making the following function calls.
glEnable(GL_STENCIL_TWO_SIDE_EXT);
glDisable(GL_CULL_FACE);Using the GL_EXT_stencil_two_side extension, an uncapped shadow volume is rendered using the following code, which uses depth-pass stencil operations.
glActiveStencilFaceEXT(GL_FRONT);
glStencilOp(GL_KEEP, GL_KEEP, GL_INCR_WRAP_EXT);
glActiveStencilFaceEXT(GL_BACK);
glStencilOp(GL_KEEP, GL_KEEP, GL_DECR_WRAP_EXT);
DrawShadowVolume();A capped shadow volume is rendered using the depth-fail stencil operations shown in the code below.
glActiveStencilFaceEXT(GL_FRONT);
glStencilOp(GL_KEEP, GL_DECR_WRAP_EXT, GL_KEEP);
glActiveStencilFaceEXT(GL_BACK);
glStencilOp(GL_KEEP, GL_INCR_WRAP_EXT, GL_KEEP);
DrawShadowVolume();Note the use of the GL_INCR_WRAP_EXT and GL_DECR_WRAP_EXT stencil operations. These are provided by the GL_EXT_stencil_wrap extension to OpenGL and allow stencil values to wrap when they exceed the minimum and maximum stencil values instead of being clamped. These operations are necessary because we do not know in what order the polygons belonging to the shadow volume will be rendered and we must account for the possibility that the stencil value for a particular pixel could be decremented before it is incremented.
Scissor Optimization
When using an attenuated light source, it is usually convenient to define a range r beyond which the light source does not contribute any illumination to the world. Although this is not a physically correct model, using an attenuation function that vanishes at a distance r from the light’s position allows us to quickly cull any light source whose sphere of illumination does not intersect the view frustum. When a light source’s sphere of illumination is visible, the area within the viewport that could possibility be affected by the light source may not be the entire viewport. By projecting the sphere of illumination to the image plane and using the scissor rectangle to limit our drawing to the projected area of influence, we can avoid a significant amount of superfluous rendering of both shadow volumes and illuminated surfaces.
Suppose that we have a point light source whose center lies at the point L in eye space and whose range is r, as shown in Figure 8. We wish to find four planes, two parallel to the x-axis and two parallel to the y-axis, that pass through the camera position (the origin in eye space) and are also tangent to the light source’s bounding sphere. Once these planes have been determined, we can locate their intersections with the image plane to find the rectangular boundary of the projection of the light source’s bounding sphere.
Figure 8. For a point light source at the position L having range r, we calculate the four planes that pass through the camera position C and are tangent to the light’s sphere of illumination. By calculating the intersection of each tangent plane with the image plane lying at a distance e from the camera, we can limit our drawing to an area smaller than the full size of the viewport.
We assume that the tangent planes parallel to the y-axis have a unit-length normal vector N whose y-coordinate is zero. Since the planes pass through the origin, each can be represented by a 4D vector T = <Nx,O,Nz,O>. We wish to calculate values of Nx and Nz such that the following conditions are satisfied.
(24)
(25)
By expanding the dot product and rearranging slightly, we can rewrite Equation (24) as
(26)
Squaring both sides of Equation (26) and making the substitution N2z=1-N2x, we have
(27)
This can be rewritten as a quadratic equation Nx in as follows.
(28)
The discriminant D is given by
(29)
D<0 precisely when L2x+L2z<r2 (i.e., when the origin falls within the projection of the sphere onto the x-z plane). When this happens, we know the light source’s bounding sphere fills the entire viewport and we do not continue.
If D>0, then we can solve equation (28) using the quadratic formula to obtain
(30)
This gives us two values for Nx. The corresponding values for Nz are calculated by making a small adjustment to Equation (26):
(31)
We only want to consider planes whose point of tangency with the light source’s bounding sphere lies in front of the camera. As illustrated in Figure 8, the point of tangency P lies in the plane <Nx,0,Nz,0> at a distance r from the point L, giving us the following two equations.
(32)
(33)
Equation (33) can be expanded to
(34)
Using the Pythagorean theorem, we can replace P2 with L2-r2 to obtain
(35)
For the point P to lie in front of the camera, we must require that Pz<0. Since the tangent plane is parallel to the y-axis, the values of Py and Ly are equal and the quantity L2y cancels in Equation (35). By solving Equation (32) for Px, we can make the substitution
(36)
in Equation (35) to arrive at the following equation written completely in terms of the unknown Pz.
(37)
Solving for Pz, we have
(38)
For any tangent plane <Nx,0,Nz,0> calculated using Equations (30) and (31), we calculate the corresponding value of Pz using Equation (38). If Pz < 0, then we have found a plane that may allow us to shrink the scissor rectangle. We now need to determine where the tangent plane intersects the image plane.
As shown in Figure 8, the image plane is perpendicular to the z-axis and lies at a distance e from the camera. On the image plane, the area of the viewport corresponds to x-coordinates in the range [-1,1] and y-coordinates in the range [-a,a], where a is the aspect ratio given by the height of the viewport divided by its width. Any point Q lying in the image plane has coordinates <x,y,-e>. A point Q lying in the plane tangent to the light source’s bounding sphere satisfies N · Q = 0, so we can solve for x:
(39)
This x-coordinate can be mapped to the viewport coordinate x' using the formula
(40)
where l is the left edge of the viewport and w is the viewport’s width, both in pixels.
Given a value x' calculated using Equation (40), we need to determine whether it represents a left-side boundary or a right-side boundary. This can be accomplished by plugging the value Pz given by Equation (38) into Equation (36) to obtain Px. If , then represents a left-side boundary because the point of tangency falls to the left of the light source. If Px>Lx, then x' represents a right-side boundary. Since the value may lie outside the viewport (if x Ï [-1,1]), we calculate the left and right edges of the scissor rectangle as follows.
(41)
The two tangent planes parallel to the x-axis are found in an almost identical manner. Each of these planes is represented by a 4D vector <0,NyNz,0>, whose nonzero components are given by the following formulas.
(42)
The z-coordinate of each corresponding tangent point is given by
(43)
If Pz<0, then the y-coordinate where each plane intersects the image plane is given by
(44)
where the viewport’s aspect ratio a has been added to the denominator. Finally, the viewport coordinate y' is calculated using the formula
(45)
where b is the bottom edge of the viewport and h is the viewport’s height, both in pixels.
To determine whether y' represents a bottom-side boundary or a top-side boundary, we calculate the y-coordinate of the point of tangency using the formula
(46)
If Py<Ly, then y' represents a bottom-side boundary. If Py>Ly, then y' represents a top-side boundary. As with the left and right sides, the values of y' should be clamped to the viewport’s range as follows.
(47)
Using the values given by Equations (41) and (47), the OpenGL scissor rectangle is enabled and set to the appropriate values using the following function calls.
glEnable(GL_SCISSOR_TEST);
glScissor(scissor.left, scissor.bottom,
scissor.right - scissor.left,
scissor.top - scissor.bottom);The scissor rectangle affects the clear operation as well, so once rendering has been completed, one should either disable the scissor test or set the scissor rectangle back to the entire viewport rectangle by making the call glScissor(l, b, w, h).
Conclusion
The techniques described in this article can be used to efficiently render the shadow volumes needed to display a fully shadowed scene in real-time using stencil operations. Future graphics hardware will undoubtedly incorporate greater shadow volume functionality that will relieve the CPU from some of the work that it currently has to do, but the ultimate determination of speed will be innovative methods for minimizing the number of shadow volumes that must be rendered in the first place. Achieving high frame rates for complex scenes having multiple light sources is now the goal of larger-scale optimizations, and this is currently a hot area of 3D graphics research.
For Further Information
The following is the original paper discussing shadow volume capping and depth-fail stencil operations
Everitt, Cass and Kilgard, Mark J., “Practical and Robust Stenciled Shadow Volumes for Hardware-Accelerated Rendering”, NVIDIA Corporation, 2002.
Mathematical derivations of different bounding volume tests that can be used to determine whether an object’s shadow volume might intersect the near rectangle can found in the Visibility Determination chapter of the following book.
Lengyel, Eric, Mathematics for 3D Game Programming & Computer Graphics, Charles River Media, 2002.
Information about the OpenGL extensions used in this article can be found at the OpenGL Extension Registry website:
http://oss.sgi.com/projects/ogl-sample/registry/
Read more about:
FeaturesYou May Also Like