Creating an Event-Driven Cinematic Camera, Part One 2

In the beginning, Auguste and Louis Lumiere made their first short movies without changing the position of the camera. It would take others, such as the magician Georges Melies, to stop and move the camera to create more dynamic scenes than could be done with a stationary, continuously running camera. Over the next century, cinematographers and editors have learned the best ways to film, cut, and transition between different shots to make the movie experience larger than life.

When it comes to camera setup, the dynamic nature of games puts us back to the days of Lumiere. With minimal or no control of the placement of the actors in a game, camera shots are often set as stationary or dragged behind one of the actors. Here and there, we see games that try innovative camera techniques — some that work and others that do not. One way to improve the chances of success is to take the film industry’s century of experience and adapt it to our industry.

One method at our disposal in games is to create a system that automates camera placement and scene transitions (similar to the jobs of the cinematographer, director, and film editor on a major film production). In this, the first of a two-part series of articles on this subject, I’ll look at automating the work the cinematographer does in setting up cameras to capture the best view of a scene. This will lay the groundwork for choosing among available scenes and camera shots required by the director and editor, which I will cover largely in part two.

Describing the Shot

Since the position and orientation of the actors is not known ahead of time, a method of describing the shot without exact positioning information is necessary. In order to arrive at a suitable set of parameters, let’s look at the basic rules and descriptions that a cinematographer follows when setting up a camera shot. We are not searching for a complete description of how the shot is set up, but just for enough information from which to establish a position and orientation for the camera. For example, while we may eventually wish to implement different camera filters for interesting effects, what we care about now is mainly the field-of-view for the camera.

The most important rule of cinematography is called the 180-degree rule: The camera should not cross the line of action. The line of action is an imaginary line that partitions a scene into two distinct areas, usually going through the main actors or in the direction of movement. By not crossing the line between shots, a scene’s screen direction and space is preserved. This idea can be extended to account for the three-dimensional nature of certain games by using a plane to partition space rather than just a line. This information is constant across all or several of the shots in a scene.

Once the line of action has been established, camera placement within the valid area follows what is known as the triangle system. Figure 1 shows the four basic camera positions for two actors: standard, over-the-shoulder, point of view, and profile. Each of these layouts has the same camera at the top point of the triangle, which is used for the establishing (or master) shot. The remaining cameras are meant to favor one actor over another. Figure 1 shows the approximate locations of the cameras on a two-dimensional plane, leaving the need for another parameter to describe the height or vertical angle of the camera.

Two remaining parameters involve the framing of the actor or actors on the screen. The first of these parameters is the shot size, which will determine the distance of the camera from the actor. Figure 2 shows the visible portions for a human actor in the common shot sizes. In addition to these shots, the long shot frames the actor with plenty of space between the edge of the screen and the actor. The other parameter determines the emphasis given to one actor or another, or the approximate screen space taken up by each actor. This information should be sufficient for us to move on to laying out the actual data structure and working out the equations for determining the final position and orientation. From here I’ll assume a basic knowledge of vector math, otherwise, you may wish to refer to Eric Lengyel’s Mathematics for 3D Game Programming and Computer Graphics (Charles River Media, 2002) or other similar graphics text.

Setting the Scene

The first data structure we need is the scene, which persists across several individual shots. In a scene, we are primarily concerned with the actors and therefore need a list of the scene’s actors. The other important part of a scene is the line of action, discussed earlier, which will be stored as a matrix for reasons I will discuss shortly. This means a scene will store data similar to:

class scene
{
// ...
list actors;
matrix line_of_action;
};

Let’s take a closer look at the actor data and see what we will need to know about each actor. To simplify framing of the actor, we will consider only bounding spheres. However, we do need to use two spheres to model a human actor properly. The first sphere encompasses the entire actor, while the second surrounds only the head, or some other significant area for nonhuman actors. Finally, the orientation of the actor is important and should be included in the final data structure similar to this:

class actor
{
// ...
matrix orientation;
sphere body;
sphere head;
};

Now we turn to computing the line of action. As discussed earlier, we can consider this more a plane of action and therefore conveniently store it as a matrix. Although it’s possible to store it more succinctly, the full matrix provides convenient directional vectors and is a standard data structure used in most games. The exact line of action depends on the number of actors in the scene; here I’ll be considering either one or two actors. For one actor the line of action is the vector in the direction the actor is facing, and for two actors the line of action goes from the primary actor to the secondary actor. Use these as a right-vector for the matrix, and form the rest of the matrix using the average up-vector of the actors as a reference:

Emphasis

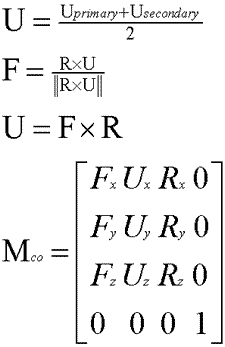
The first parameter we need to look at in the individual shot is the emphasis, because it will affect several of our following calculations. However, before we handle the emphasis we must choose what we want to emphasize. For our purposes, I’ll assume that you can focus on the primary actor, secondary actor, or both. The focus is the center of the selected actor, which I will describe how to calculate when I talk about size. There are two ways we could handle focusing on both actors, the simpler of which is to use the midpoint between the centers. Later, I will discuss a slightly more complex approach that is particularly useful for over-the-shoulder camera shots.

The emphasis chosen specifies where on screen we wish to place the focus. Full-screen emphasis would place the focus in the center of the screen, two-thirds emphasis would place it at one-third of the way across the screen, and half emphasis would place it at one-quarter of the way across the screen. With that in mind, we need to convert the emphasis specification to values we can use in our calculations.

Table 1. Values for each emphasis type, where FOV is the
horizontal field of view for the camera.

The three important values are the angle formed between the ray to the emphasis and the center ray, the angle between the emphasis of the main actor and the emphasis of the second actor (if any), and the distance from the camera to the intersection of the emphasis ray with the view frustum plane one unit from the camera. Table 1 shows the three main emphasis types and their respective values. With these, we are ready to move on to some actual calculations, starting with the camera distance from the focus based on desired size.

Table 2. Interpolation values for shot sizes.

The first step to computing the distance from the focus is to determine the part of the actor to show. At the same time, we can compute the exact location of the focus. This location is the same as the center of the actor mentioned earlier. To do all this, we bring the head and body spheres into play by interpolating between them based on the desired shot size. Table 2 shows the interpolation percentages for several common shot sizes. Take these and plug them into the following equations:

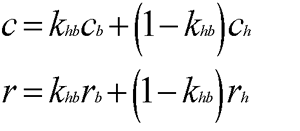
This gives the desired center, or focus, and radius values. Table 2 also gives the percentage of the screen we wish the actor to occupy, which equates to the ratio of the radius to half the screen height. Now we can form two similar right triangles, one using the radius as the far side and one using half the height of the frustum view plane one unit from the camera. Respectively, the adjacent sides are the distance we are seeking and the length value from Table 1. Since the triangles are similar, we know the following ratios are equal:

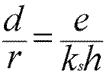
Here, we can obtain h by taking the tangent of half the vertical field of view. Solving for the distance we get:

Angle

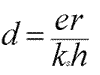
We start with the line-of-action orientation matrix, M_CO, as our initial camera matrix before the angle changes are applied. Next, we need to determine the initial offset for the camera based on the distance we just computed:

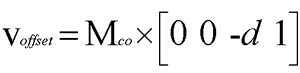
With this as a starting place, we can break the remainder of the angle changes down into three separate rotations:

1. Rotate M_CO and v_offset around the up vector of M_CO by a.
2. Rotate M_CO and v_offset around the right vector of M_CO by b.
3. Rotate M_CO around the up vector of M_CO by q.

Now let’s go over how to compute each of these angles. For the first pass, we start with a simple version of a used when we only care about ensuring that one of the actors is onscreen. The angle is chosen based on the shot type we want from those shown in Figure 1, although more shot types could be added. Table 3 shows the angles to use for each shot type.

Table 3. Shot angles.

The second angle, b, is the desired vertical angle from which to view the scene and should be between –90 and 90 degrees. That leaves us with only q to determine, which is based on the emphasis angle, q_e. The only modification is that we use –q_e if we are looking at the primary actor and q_e if we are looking at the secondary actor.

Finally, add v_offset to the focus location to get the final camera position. The orientation of the camera is M_CO. That completes the basic shot. Let’s look now at an alternative for shooting two actors that is more complex but produces a better shot.

Two Heads Are Better Than One

Sometimes you want both actors in the shot, for which the preceding methods didn’t work. An improved method for framing in this case only need modify how a is calculated when working out the camera angles. Figure 3 is the desired result, and if we apply the law of sines to this, we get:

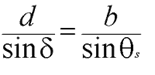
From this we derive:

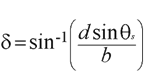
Knowing that the angles in a triangle total 180 degrees, we get the following equation for a:

Handling Obstructions

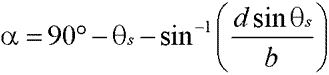
The main problem that arises once a camera shot has been calculated is an obstructed view of the actor or actors in the scene. There are a number of ways to handle this, of which I’ll examine two of the most useful.

The first method is advantageous if the scene involves moving elements or a moving camera and you wish to ensure the actors are visible throughout. Start by rendering the actors first, storing the area of the screen and distance from the camera in which each actor is rendered. Now render the rest of the scene, skipping any objects that overlap one of the actors closer to the camera than that actor. Now go back and sort these actors from back to front and render them as translucent. This technique can be fairly expensive, especially for longer shots and complex scenes.

There is a less expensive technique that we can employ during the setup of the shot. To use this method, you must determine if a shot is obstructed once it’s chosen. A simple method is a line intersection test that uses a set of lines going from the camera to the bounding sphere of the actor, similar to those in Figure 4. Other patterns of lines can be used as long as the coverage is sufficient for larger objects. If there is an obstruction, an ordered set of shot alternatives are tested until one of the shots is unobstructed. This method allows smaller or moving objects to obstruct parts of the actors, but it is generally faster and less artificial than using translucency.

On the Move

Movement is a very important part of games, and we would be lax if we did not consider it. First, we must consider how to handle moving actors. When we are focusing on only one actor, a simple solution is to follow that actor. If we cut to a different camera angle, we must obey the line of action at that time. However, it’s not a problem if the camera rotates with the actor as long as the line of action is updated to reflect the new heading.

What happens when we are looking at two actors? There are several options, depending on the circumstances. If the actors are both known to be traveling in the same direction, the camera and the line of action can simply follow them as they did with only one actor. Another possibility, which could also be used with a single actor, is to let them travel out of frame before establishing a new camera shot and a new scene with a different line of action. This method allows the actors to move around in the shot as long as they do not stray too far. Cutting to a new scene is the only option if the actors travel in opposite directions, and the new scene will likely not have both actors in it.

One final form of movement that should be mentioned is camera movement. Up until now, we have treated shot changes as cuts, moving instantly from one camera position to the other. In some cases, a better or more interesting transition can be achieved by moving the camera smoothly from one position to the other. You could also use this to establish a new line of action within the same scene, but this should be used rarely.

What’s Next?

I have covered the basics of setting up a shot using common cinematography techniques, but there is much more that can be learned from the film industry. For example, I handled the most common cases of one or two important actors in a scene. There are occasions when three or more actors are important to a scene. See the For More Information section for additional resources on cinematography.

Another aspect that I have not discussed is the camera filter, which can add certain effects and moods to the scene. I dealt with one camera change, the field of view, because it was very important to position. However, it is also possible to perform color filtering, depth of field, and other more complex effects to add certain qualities to a shot. You should experiment with these effects to see if you can add that extra touch to your game.

A more complex issue that is rarely addressed in games currently is cinematic lighting. This is an extremely important part of filmmaking and can lend a professional touch to any scene. While lighting principles are well known in the film industry, in the game industry they are normally only applied to movies outside of the gameplay. Similar principles as those in this article could be used to help automate some of the lighting decisions for games, adding extra realism and production quality to a game.

However, the largest area I haven’t touched on yet is deciding what shot to use for a given situation. With the addition of hints from programmers and level designers, it’s possible to automate the process of shot selection. This involves deciding among available shots, picking transitions, and changing scenes when appropriate. In the next installment, I’ll take a closer look at this important part of our work on automating interactive cameras.