Trending
Opinion: How will Project 2025 impact game developers?
The Heritage Foundation's manifesto for the possible next administration could do great harm to many, including large portions of the game development community.

Featured Blog | This community-written post highlights the best of what the game industry has to offer. Read more like it on the Game Developer Blogs or learn how to Submit Your Own Blog Post
Evolutionary algorithms can optimize game parameters by simulating various scenarios, enhancing design, especially for complex games.
August 13, 2024

Imagine a multiplayer online game, such as a MOBA, where players choose from a roster of characters or a real-time strategy game with various unit types players can recruit from.
It is exceptionally challenging and tedious to balance the classes or units, so no single strategy becomes overwhelmingly dominant or completely useless. However, the objective of having properly balanced parameters in a game is crucial to make it engaging, with diverse gameplay and -- ultimately -- successful. Not to mention that properly balanced online multiplayer games have the potential to be played in competitive or even e-sport settings.
Imagine a battle encounter in an RPG game, in which you want experienced players to win by a narrow margin. This can be a design goal to create suspense as the outcome remains uncertain until the very end. As the previous one, this task also requires finding the correct set of parameters from a vast, multi-dimensional space of possible values.
In both examples, properly used evolutionary algorithms can support you. More examples of use cases will be provided in the “Designing a Good Fitness Function��“ section of this article.
We have conducted a very simple proof of concept. Earlier, before even applying evolutionary algorithms, we had developed a simple demo called Grailbots, which demonstrates one of the techniques offered by Grail. In short, Grail (https://grail.com.pl/) is a middleware designed to implement AI in games using C++ or C#. It is suitable for various engines including custom ones, Unity, or Unreal.
Grailbots showcases the Utility AI technique implemented in Grail. This demo features two teams controlled by AI:
Grailbots - a team of four “smarter” soldiers whose behavior is implemented using Utility AI.
They resemble agents that could also be controlled by humans in a real-game.
Enemies - these appear in three waves and represent simple mobs with straightforward assault behavior, taking the shortest path to the Grailbots. They resemble hordes of zombies or other attacking crowds (although less numerous) as in tower defense and bullet hell games.
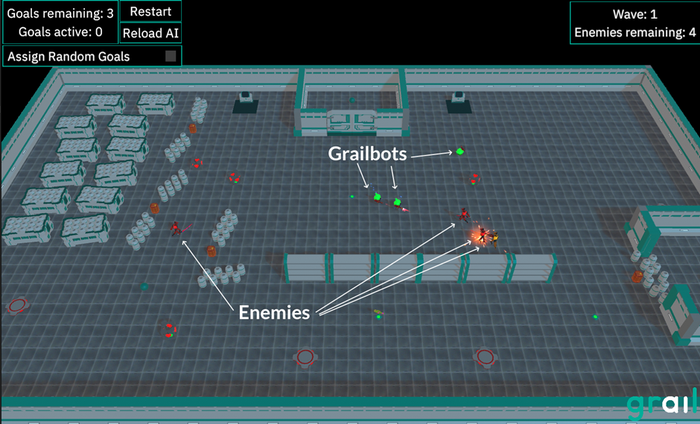
Screenshot from the Grailbots demo (simple sample project). In this situation, one Grailbot has already been killed by the Enemies.
For this proof-of-concept, our aim was to select the set of parameters of Grailbots and Enemies, such that the Grailbots would typically win by the smallest possible margin. Ideally, the best outcome would be having just one Grailbot surviving with 1 HP after the three enemy waves.
This objective may sound artificial, but our idea was to test whether a design goal of this complexity could be feasibly achieved automatically using evolutionary algorithms.
In the following sections, we will continue to explore this use case but first let us provide a short background on this area. The Grailbots example will be continued in the final section.
Evolutionary algorithms (EA) draw inspirations from nature. In particular, the fundamental concepts that underpin their idea are natural selection, adaptation to the environment and survival of the fittest. These concepts were introduced in 1859 by Charles Darwin in a book titled “On the Origin of Species by Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life”.
The classic way of solving problems on computers involves writing sequences of specific instructions. This significantly differs from evolutionary algorithms, which are an example of an Artificial Intelligence (AI) technique, albeit not as popular in recent years as Machine Learning. In EAs, as well as in broader AI, programmers only specify some measure of the quality for the end result without explicitly programming the way to achieve it. The solution is found automatically using a general, problem-agnostic approach.
They also belong to subclasses of AI called:
Computational Intelligence
Metaheuristics
Evolutionary Computation
In EAs, a population of potential solutions to a problem is maintained. The initial population contains weak solutions, often generated randomly or using a simple heuristic. These potential solutions are then subjected to a process mimicking natural evolution. They can reproduce and mutate. The new offspring replace some or all of the previous generation, forming a new population. There is also a concept of fitness, which plays a key role in selection of the individuals for the new population. Some of the basic notions you should know are presented in the next section.
The evolutionary computation encompasses several techniques inspired by natural evolution. For example:
Evolutionary algorithms: the topic of this article
Genetic algorithms (GA): similar to EAs, but they assume a binary-string encoding
Evolutionary strategies: iterative search method, which is often based on evolving a single solution
Genetic programming: evolving computer programs; they use dedicated representations
Memetic algorithms: also referred to as cultural algorithms, they combine GAs or EAs with local search
Differential evolution: a R^n -> R function optimization technique, which uses specific methods of combining existing solutions.
Individual - represents a single complete candidate solution to a problem that is solved using evolutionary computation. Individuals form a population and undergo evolutionary operations.
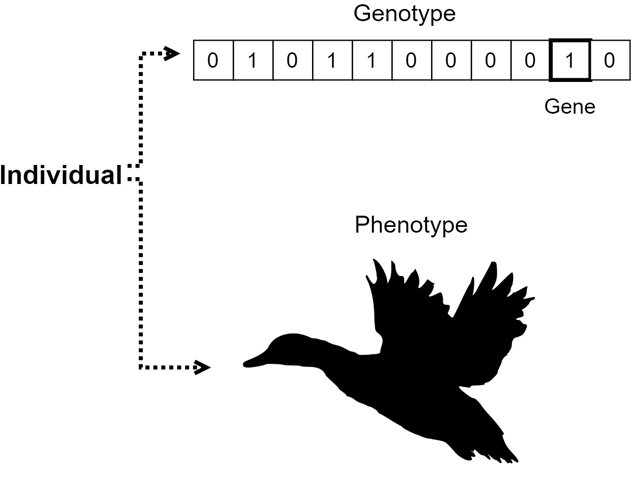
Genotype (chromosome) - represents the genetic encoding of the parameters of the individual. This is the representation used for evolutionary operations. For example, in genetic algorithms, a binary string is a commonly used encoding. One of the benefits of such an encoding is the ability to use the standard, well-established genetic operators with it.
Gene - a fundamental unit and building block of a genotype. Genes are typically located at fixed positions within a chromosome like cells in a vector.
Phenotype - this is the decoded representation, which is the actual form in which the solution is used in the real world. This representation is also referred to as “expressed” or “observable”. It contains features that are observable consequences of a particular genotype. Using the analogy to nature, while the genotype can be likened to a DNA sequence, the phenotype is the actual living organism that possesses this DNA sequence.
Population - a collection of individuals that together undergoes the evolutionary process. Individuals within the population compete with each other and may recombine. In other words, a population represents all potential solutions maintained at a given moment in the algorithm.
Fitness - assigned to individuals, is the numerical assessment of the quality of the candidate solution represented by the individual. Fitness is calculated by the fitness function and is typically defined as a floating-point number.
Crossover (recombination) - an operation that combines genetic information from two (or more in rare cases) parent individuals to create one or more offspring, analogous to biological reproduction. Many common crossover operations have been proposed. Most of them combine parts of the parents' encodings in some way with stochastic elements such as choosing the crossover point at random. Typically, fitter individuals (with higher fitness) have a higher chance of being selected for reproduction. Thus, crossover is often associated with exploitation, as it aims to exploit parts of the most promising candidate solutions.
Mutation - another genetic operation that introduces small random changes to individuals. Unlike crossover, mutation requires only one parent, subsequently mutates. Also, unlike crossover, mutation is typically applied with a very small probability (e.g., 0.05 - 0.1) to each individual. Mutation is often associated with exploration as random alterations to the encoding enable exploration of unknown regions in the solution space.
Children (offspring) - new individuals created through the application of genetic operations (crossover and mutation) to parent individuals.
Selection - the procedure of choosing individuals from the current population, including the results of mutation and recombination, for the next population. The next population will serve as parents in the next iteration. There are many selection methods, but most of them select individuals with higher fitness with higher probability.
Elitism - a mechanism that allows the best-evaluated individuals from the current (parent) generation to survive into the next generation without any change. Such individuals are called the elite ones. This mechanism ensures that the best solutions are not lost due to randomness introduced by the evolutionary operations.
Epoch - one iteration of the evolutionary algorithm. It consists of evaluating the population, applying the defined genetic operations (mutation and crossover), and selecting the individuals for the next population.
"Handbook of Evolutionary Computation" edited by Thomas Bäck, David B. Fogel, and Zbigniew Michalewicz. Published by Taylor & Francis Group. ISBN: 978-0-7503-0392-7.
"Evolutionary Computation: A Unified Approach" by Kenneth A. De Jong. Published by MIT Press. Online ISBN: 9780262255981.
“Evolutionary Computing: The Origins. In: Introduction to Evolutionary Computing” by Agoston E Eiben and Jim E. Smith. Published by Springer, Berlin, Heidelberg.
DOI: https://doi.org/10.1007/978-3-662-44874-8_2
Let’s suppose you are deliberating whether some of your game’s parameters could be optimized using evolutionary algorithms.
There are two main prerequisites for this:
You are able to come up with a fitness evaluation function that will assign the quality to your sets of parameters.
Your game is simulable.
The next two sections will address these topics, respectively.
Designing an effective evaluation function is often the most challenging aspect when applying evolutionary algorithms for optimization. This requires thinking about the desired outcomes in numeric terms. The value of the fitness function indicates the extent to which your design goals have been achieved.
The fitness function can be categorized as:
Deterministic - where a given phenotype consistently receives the same fitness score. For example, consider the problem of finding the shortest path in a graph with the fitness function defined as the inverse of the total distance. The same paths have the same total distance and thus the consistently the same fitness value.
Non-deterministic - where different evaluations might assign varying fitness scores to the same individual due to random elements in the calculation procedure.
Additionally, the fitness function can be:
Direct (absolute) - if it assesses an individual directly based on its attributes and returns its quality without requiring the comparison with other individuals. An example is the inverse of total distance in the shortest path problem, where the fitness directly depends on the path.
Relative - where fitness results from interactions between two or more individuals in the population. For instance, consider a tournament setup for each individual in a population, where each participant competes in five 1-on-1 matches against randomly selected opponents. The fitness value is then derived from the number of wins divided by five. This is an example of both relative and non-deterministic fitness function.
The deterministic & absolute fitness functions are the best in terms of speed and convergence of evolutionary algorithms. However, in game development, you will typically be dealing with non-deterministic & relative ones.
Below, I am showing boxes presenting some examples and inspirations for your games.
The first row of each box specifies the type of game and the optimization objective within it.
The second row describes the idea for the evaluation function.
Optimizing parameters of weapons in an FPS game. |
Fitness calculation involves a series of head-to-head battles between two standard bots. The bots are the same, but they use different fixed weapons, e.g. Heavy Rocket Launcher and basic Pistol. For each pair of weapons, the designers specify the expected win-rate. For example, the Heavy Rocket Launcher should win a fraction of 0.9 (90%) of the time against the basic Pistol. The fitness function assigns: 1.0 - | actual_winrate - expected_winrate| Such a process may either optimize only two or multiple weapons at once. In the latter case, the fitness function can use a sum or a root mean square error (RMSE) calculated for each weapon pair. |
Generating interesting map layouts from predefined components (blocks) in a dungeon-crawler or rogue-like or action RPG game. |
We can assume a maximum completion time for a dungeon (a timeout). If a bot is not able to complete the dungeon within the time limit, the fitness value is zero. Otherwise, the fitness value can be the total completion time in seconds or the number of interactions along the way. In general, designers may define a number of quality measures for a dungeon. The fitness function can then be the portion of the satisfied quality measures divided by the total number of measures. |
Finding the parameters of units (such as recruitment cost, movement speed, subset of abilities, offensive and defensive statistics) in a real-time strategy (RTS) game. |
Let’s assume that the game features 3 unique factions: A, B, and C. Each individual encodes the parameters of units of each faction. It is evaluated in each iteration based on six matches:A vs B x2 B vs C x2A vs C x2 The optimal winrates of players would be [0.5, 0.5, 0.5]. We can calculate the RMSE of the actual winrates, invert it and call it the fitness value. Additionally, we can incorporate a second factor, added with a small weight, that gives bonds points based on how many of the units have been actually used in these games. |
In a multiplayer game featuring a map and resources, optimizing the locations and quantities of resources to ensure balanced gameplay for each player, regardless of other starting parameters (e.g., spawn points, types of factions or units). |
Fitness function: similar as above, but individuals encode different sets of parameters. |
In a roguelike bullet hell game (such as Vampire Survivors or Halls of Torment), finding various sets of parameters [the number of enemies, the composition of enemy units], which will push players to their limits. |
If the player lost: the fitness value is zero. If the player won: the fitness value can be equal to the number of enemy units or to (max_player_health - remaining_player_health). They will prioritize different aspects - either the sheer number of enemies (but keeping the player alive) or the minimal victory over them. |
In a racing game, constructing tracks from predefined building blocks (e.g. specific curves) that will result in the highest lap times while preserving the constraint of each lap being no longer than 5 km (~ 3.1 miles). |
If the lap is longer than 5 km: the fitness value is zero. Otherwise, spawn a standard driving avatar (controlled by AI) and make it race on the track. The fitness value is equal to the number of seconds it took to complete the lap. Incidentally, this process can test whether the racing AI works properly, as anomalously large times can be detected. |
In a platformer game, optimizing the gravity parameter. |
During the fitness calculation, we might test: If the levels cannot be completed, the fitness score is zero. Otherwise, the fitness score is determined by how well the distribution of jump difficulty matches the design objectives. |
In economic games, optimizing in-game economies, including pricing, supply and demand, and reward structures. |
The fitness function can be defined to ensure a balanced and rewarding economic model. Game designers may define some rules about the model and the fitness function may test, through simulations, how well or how many of these rules are satisfied. |
Fine-tuning the shooting accuracy of bots of different difficulty levels in a First-Person Shooter (FPS) game. |
Let’s assume that each individual encodes the shooting accuracy parameter values of bots of different difficulty levels. For each of the bots, we do tests on a few levels against a special enemy bot that only runs at full speed and additionally jumps at random from time to time. In fitness calculation, we test how the accuracy parameters reflect the actual in-game shooting accuracy of the bots. The closest they match, the higher the fitness. This optimization is suitable for situations, where it is not exactly clear how a certain parameter will translate to the behavior in the actual game. |
In general, this evaluation procedure may involve human players but this makes both the implementation non-standard and the process to take extensively long.
It would be best if you could define an evaluation function that only requires to run bots.
What if you can’t?
What if you really need to evaluate your game against humans?
In such a case I would recommend defining the fitness value of a given individual (representing a given set of parameters) as an average value of outcomes from games played by humans against this particular individual. By doing it this way, we can compare results against a hopefully normal distribution of players and the more human players will play, the more confident the fitness value will be.
Let us estimate the effort.
The number of evaluations needed depends on the number of children produced in each iteration and the number of iterations.
The population size should depend on the problem complexity, but I recommend having a number between 60 and 300, because these are the sizes tested the most in various problems in the literature. For the number of iterations, I recommend from 40 to 200.
Let’s make a modest assumption of 80 iterations and 60 children produced per iteration. This requires 4800 evaluations, where each evaluation will be typically a game against a human player.
Let’s assume that one game episode lasts for 30 minutes making the whole workload equal to 2400 man-hours. Assuming an 8-hour work day, it totals to 300 mandays. This is expensive but doable given enough number of participants and a parallelized setup.
However, bear in mind that we have made low-end assumptions about the population size and the number of iterations. I really recommend setting the process using exclusively bots.
After reading the previous section, it is clear by now that most fitness evaluation functions for our purposes will require the ability to perform a vast number of simulations of the game.
To provide this ability, make sure that:
You are able to perform many simulations that start from a given initial situation.
You either need to implement a robust state loading system or perform a hard reset, but pass the information about the current individual(s) to evaluate. In the latter case, your evolutionary algorithm object must persist between the restarts, or be written and read from the disk or executed on an external server that communicates with the machine that performs the simulations.
You are able to dynamically apply all the parameters encoded in the individual to the game.
You make the simulations as short as possible. This includes defining scenarios (episodes) within the game and optimizations discussed below.
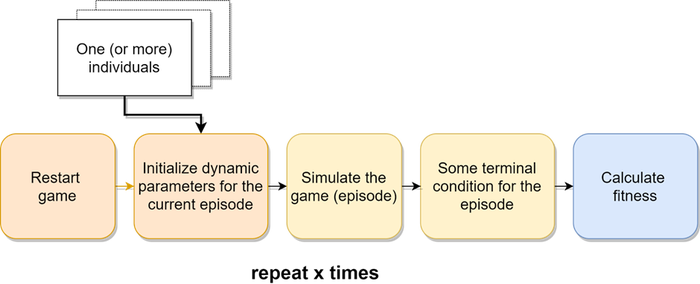
Headless simulations: if the simulation only involves bots, consider creating a headless version of the game, i.e., one without graphical rendering. This should be done unless graphics are essential for the proper functioning of the game. Excluding human players eliminates the need for graphics, which can significantly speed up the process.
Speed up time: try increasing the internal clock of the game to make it run faster. Again, this is only feasible in simulations without human players. However, do it carefully, as sometimes, increasing the rate at which the game is played may interfere with the physics calculations. Also, this acceleration is constrained if the bots in the game require a minimum amount of time to “think”. In practice, it is typically possible to increase the speed by at least a factor of 2-3.
Save and load of the EA state: implementing the functionality to fully serialize the current state of a running EA algorithm, including the current population, enables the process to be split across multiple sessions. This is particularly useful in scenarios, where computing resources are not always fully available or when human players are involved in the loop. For example, if human players are required to play the game, some machines can be allocated for this purpose. Whenever a player is ready to play, the system will load the current state of the EA. The player may then advance the progress of the algorithm by some steps, depending on the number of games played.
Parallelization: while not required, it will make the process significantly faster. EA algorithms are very convenient to parallelize and they can benefit a lot from this optimization. Parallel computing can be implemented either on a single machine (taking advantage of CPU threads) or many machines.
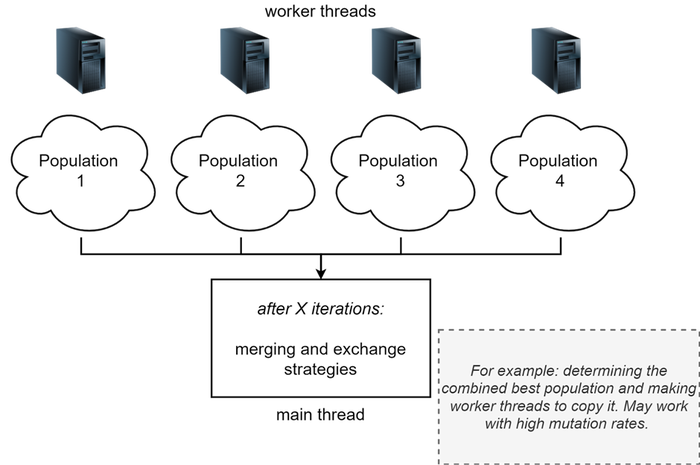
There are a lot of strategies for parallelizing the EAs. The most common ones are:
Parallelization of evaluating individuals: while the main thread handles a single population and oversees the execution of the EA (Evolutionary Algorithm) at a high level, worker machines can be assigned to assess given individuals or just specified subsets of the population. For instance, if there are four remote machines available, each can evaluate one-fourth of the population.
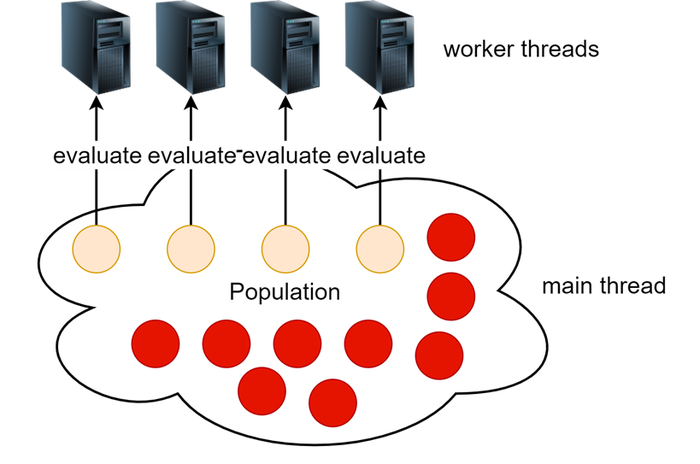
Parallel populations: another strategy involves running semi-independent EA processes, each with its own distinct population. After several epochs, these populations can undergo merging, synchronization, or interchange of individuals among them. This method is often known as the “island model”. It allows for a diversified genetic pool across different populations.
The following seven parameters have been chosen for optimization:
Health value of each Grailbot
The number of random enemies in the first wave
The number of random enemies in the second wave
The number of random enemies in the third wave
The probability that a random enemy in the first wave will be a rifleman (vs. melee soldier)
The probability that a random enemy in the second wave will be a rifleman (vs. melee soldier)
The probability that a random enemy in the third wave will be a rifleman (vs. melee soldier)
Listing 1. [C# code] Setting up the encoding and optimizable space. |
public class GrailbotIndividual : Individual { public EvoParam<int> Health = new EvoParam<int>(100, 80, 60); public List<EvoParam<int>> WaveCounts = new List<EvoParam<int>> { new EvoParam<int>(3, 5, 6, 7), new EvoParam<int>(5, 7, 8, 9, 10), new EvoParam<int>(6, 8, 9, 10, 11) }; public List<EvoParam<float>> RiflemanProbabilities = new List<EvoParam<float>> { new EvoParam<float>(0.3f, 0.5f, 0.7f), new EvoParam<float>(0.3f, 0.5f, 0.7f), new EvoParam<float>(0.3f, 0.5f, 0.7f), }; public GrailbotIndividual() { SetMemberParameterOptimizable(Health); SetMemberParameterOptimizable(WaveCounts); SetMemberParameterOptimizable(RiflemanProbabilities); } } |
This can be set up using the Grail library by inheriting from a class named Individual as shown in Listing 1. It allows to set selected member parameters as “optimizable”, meaning that they will become part of the encoding and they will be able to be changed through evolution.
These parameters must be defined as EvoParam<T> type, where T is the type of your actual parameter.
In the constructor of EvoParam you specify the domain, i.e., the available values (of type T) that the parameter can take.
Thanks to built-in implicit casting, EvoParams<T> can be used as follows:
Listing 2. [C# code] Example of working with EvoParams. |
var parameter = new EvoParam<double>(0.2, 0.5, 0.7); if(parameter*5 < 1.0) { //do something } |
Now we create the EAOptimizer object, which represents the interface of the evolutionary algorithm.
The GetRandomRealizations(...) method returns a given number of randomly generated individuals that have the same parameters structure as the one it is called on.
populationSize was set to 40
epochCount was set to 50
MutationIndividualRate was set to 0.15.
It is the expected value of the portion of the population that will mutate in each iteration.
CrossoverIndividualRate was set to 0.55
It is the expected value of the portion of the population that will produce offspring in each iteration.
ElitismRate was set to 0.1
It is the portion of the top ranked population that is guaranteed to advance to the next generation.
Listing 3. [C# code] Initializing the evolutionary algorithm object. |
var optimizer = new EAOptimizer ( new GrailbotIndividual().GetRandomRealizations(new System.Random(), populationSize), epochCount, new Crossover() { CrossoverIndividualRate = crossoverIndividualRate }, new Mutation() { MutationIndividualRate = mutationIndividualRate } ); optimizer.ElitismType = ElitismType.FITNESS_RANKING; optimizer.ElitismRate = elitismRate; |
Finally, it is time to start the evolutionary algorithm.
Our API features a RunInteractive(...) method, which allows us to integrate the game with EA.
It takes three callback functions:
OnEvaluate - invoked when EA requests to assign the fitness score to an individual.
OnTerminated [optional] - invoked when the algorithm reaches the maximum number of epochs.
OnNewEpoch [optional] - invoked when a new epoch starts.
Listing 4. [C# code] Starting the evolutionary algorithm. |
optimizer.RunInteractive(OnEvaluate, OnTerminated); |
In the provided OnEvaluate(...) method, we take the parameter values that should be verified and apply them to the game. Then, the Grailbots demo is played as it would from the beginning. Three waves of enemies, spawned with small intervals between them, are generated.
Listing 5. [C# code] Running a new episode of the game simulation. |
private void OnEvaluate(Individual individual) { currentIndividual = individual as GrailbotIndividual; // … applying parameters to the game } |
When the game is finished, we assign the fitness value to the cached individual.
We use a helper class called FitnessRepository that is responsible for updating the fitness to the average value of fitness scores obtained so far by individuals with the same encodings.
Listing 6. [C# code] Fitness update |
currentIndividual.Fitness = Score; FitnessRepository.AddSampleWithFitnessUpdate(currentIndividual); |
The score is computed as follows:
Listing 7. [C# code] Checking for game termination and calculating the fitness score. |
private bool IsEpisodeFinished() { if (Time.timeSinceLevelLoad >= Timeout) { Score = 0; return true; } if (IsGrailbotsWin()) { Score = enemyWinFitness + (1.0 - playerCharacters.Count / GrailbotsCount) + (1.0 - playerCharacters.Sum(x => x.CurrentHealth) / TotalPlayerMaxHP) * 4.0; return true; } if (IsEnemyWin()) { Score = enemyWinFitness; // = 1.0 return true; } return false; } |
Whenever our game needs to be closed, we can save the progress of the evolutionary algorithm and continue from there the next time:
Listing 8. [C# code] The save and load functionality for the evolutionary algorithm. |
optimizer.SerializeState(saveFile); … optimizer.DeserializeState(saveFile); |
In this proof-of-concept, we decided:
Not to disable rendering. This allows us to observe how subsequent iterations play out, with the currently evaluated individual shown on the screen.
To speed up the game by a factor of 1.75. This allows the process to remain observable by humans.
Not to implement parallelization.
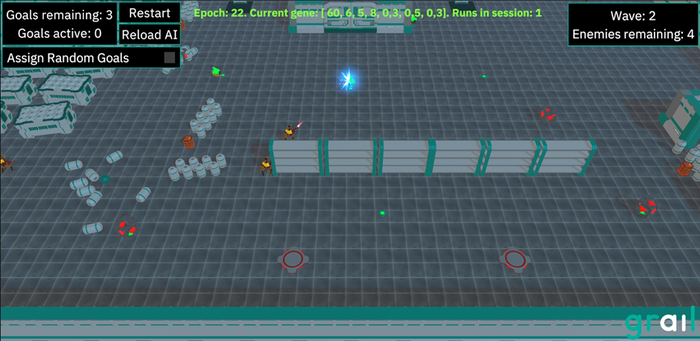
The proof-of-concept was successful. The final set of parameters determined through evolutionary optimization was:
Grailbot health: 60
Number of enemies in waves 1, 2, and 3: 5, 8, and 9 respectively
Probability of spawning a rifleman for each new enemy unit: 0.7 for all waves
Evolutionary algorithms can be applied as a tool for game developers, enhancing the process of game design and balancing. These algorithms can efficiently explore vast parameter spaces. By simulating countless gameplay scenarios and evaluating them against defined criteria, they help create more balanced, engaging, and diverse gaming experiences.
The most challenging obstacles to overcome when applying this approach are:
Distilling well-defined game scenarios from the game and optimizing them to run quickly enough to achieve the necessary scale. Evolutionary algorithms require numerous simulations!
Designing a fitness evaluation function that effectively captures the game design requirements.
While not replacing human creativity, evolutionary algorithms augment designer intuition, accelerate the balancing process, and can reveal unexpected insights. This approach is particularly valuable in complex games with numerous interacting elements, where manual tuning would be time-consuming and potentially overlook subtle interactions. Ultimately, the integration of evolutionary algorithms in game design represents a fusion of computational power and human creativity, potentially leading to more refined and enjoyable games.
You May Also Like