Author: by Bertis Rasco

There are two issues that I have noticed while playing Wii Sports. One involves bowling and one involves golf. In the bowling game I have been soundly defeated by a 7 year old. While that in and of itself is not an issue, he usually beats me by swinging his arm in a random convulsive fashion behind his back. Last time I checked, his high score was 217. The issue with the golf game is when the golf club swings backwards with respect to the motion of the Wiimote. This happens most often while putting.

These kind of issues hint at large errors interpreting the outputs of the accelerometer, estimating the Wiimote orientation, or perhaps a low battery in the Wiimote. Or all three. This article shows a useful way to improve the outputs of the accelerometers. A more complete version of this method can be used to improve the estimate of the orientation of the Wiimote. Sadly this method will not help too much with a low battery.

Inexpensive accelerometers are known for fuzzy input. An error of 5% in acceleration is enough to throw position and velocity estimates off quickly. I wager to guess that the accelerometers in the Wiimote are neither the most expensive nor the most accurate versions available. But can one get anything useful out of cheap accelerometers? Absolutely. Some good information is already pulled from the accelerometer in the Wii Sports and the Wii Play games. But can more accurate information be extracted? Definitely. But how can it be done?

One way to eke out better information from accelerometers is to use a complicated form of time dependent probability theory. This is known as Kalman Filtering. Kalman Filtering is commonly used in the navigation systems of airplanes, where knowing the location accurately, and precisely if possible, is important. Versions of the Kalman Filter are also used to estimate spacecraft and satellite trajectories.

The description, justification, and general use of the Kalman Filter is challenging, so I will merely state the results that are relevant and then go through an example. There are a few good, and more so-so books and web pages on Kalman Filtering. I list in the references only what I consider good pages, so please realize that it is a subjective list. Good luck with them [1,2,3,4]. Familiarity with differential equations, some statistics, and matrix mechanics is assumed throughout this article.

After the basic Kalman Filter equations, this article discusses a 'simple' Kalman Filter example. The 'simple' example is a one dimensional motion of an accelerometer and with ideally fairly accurate position measurements. I use the word simple only because this is as uncomplicated as Kalman Filtering gets. It does not describe the example as something that is necessarily easily understood. This example has nothing in it that explains how to extract the orientation of the Wiimote, that is the next level up in complexity of a Kalman Filter design. This example is perfect for estimating the motion of an object in one dimension, like the motion of a pool cue before it strikes the cue ball.

What is a Kalman Filter?

A Kalman Filter is a set of states, aka a vector, that approximately describe a real world system and a set of measurements that relate the set of states to a set of measurements. Well, that sounds easy enough. Here we go.

There are two basic components of the Kalman Filter equations: the model and the measurement. The model part consists of the states, or physical properties, that are used to simulate a system and the time evolution of those states. The measurement part of the Kalman Filter connects measurement inputs and the states used to describe the system.

(The Kalman Filter equations in this article are merely quoted, and not in any way, shape, or form are they derived here. Derivations of these equations do not help demonstrate why Kalman Filter is useful to locating the Wiimote. For those interested in their derivation, all of the references have something useful.)

Basic Model Equations

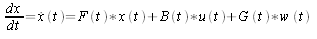(1).

Equation (1) represents the assumed time propagation of an n dimensional state vector, x(t). The vector u(t) is the control vector, and the vector w(t) is the noise vector for time evolution. The noise vector, w(t), represents how much faith you have in the time evolution equations and it can represent the unknowns in the control vector. Or both. The control vector, u(t), is an input that changes often and it is not part of the state vector because it can not be estimated. Accelerometer input is a good example of an element of the control vector, it changes from frame to frame depending on the user's motion of the Wiimote, which is not predictable in the least.

(2).

The z(t) vector represents an m dimensional measurement vector, the m by n (m rows by n columns) matrix H(t) maps the state vector to the measurement vector, and v(t) is the m dimensional noise vector related with specific measurements.

Based on these equations, there are related formulas that predict the best estimate of the state vector x(t) and of the covariance matrix, P(t). These two mathematical entities are estimates of the values of real objects in the world and how precisely the estimates are known. Since the state vector can never be known we can only make a best guess at its value and that best estimate is written as.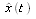

Time Propagation Equations

The first step to successfully using equations (1) and (2) are to solve them with respect to propagating them through time. Equations (3) and (4) are the time dependent solutions of equations (1) and (2).

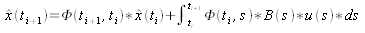(3),

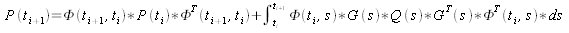(4).

The matrix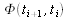is the state transition matrix defined as , with the matrix F from equation (1) (Yay, matrix exponentials!). It satisfies the relations 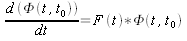and 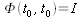, where I is the n by n identity matrix. This is a formal way to write the solution of the differential equation 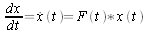. If these equations are unfamiliar to you, this article is probably not for you. If we assume Gaussian noise models, the matrix Q(t) is related to the noise vector w(t) as , where d(t) is a delta function. Different types of noise can be used in the filter, but that is a whole different can of worms and this article does not worry about it. The concerned reader is referred to the references.

One interesting feature of equations (3) and (4), is that the time evolution of the covariance matrix, P(t), does not depend on the control vector u(t), and that the best estimate of the state vector,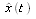, does not depend on the noise vector w(t), or equivalently Q(t).

Measurement Propagation Equations

The following equations describe how to update the state vector and covariance matrix when a new measurement is made.

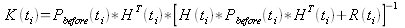(5).

Equation (5) defines the gain, K(t) in terms of the H(t) matrix defined in equation (2), the covariance matrix right before the measurement is processed, P(t), and the square noise matrix R(t) defined in terms of the measurement noise vector v(t) as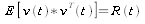. The inverse in equation (5) is a matrix inverse in general and it can be a source of significant computation. In the example the measurement is a single number so the matrix inverse is just regular division.

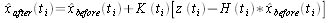(6).

Equation (6) describes how the best estimate of the state vector is updated using the gain, defined in equation (5), the measurement vector z(t), and the H(t) matrix from equation (2).

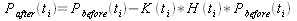(7).

Finally the covariance matrix, P(t), is updated with the gain and the H(t) matrix.

One thing that might seem strange is that in order to implement these equations no random number generator is needed. Something else that might also seem a little strange, is that the spread of the distribution of the random numbers is only used in the covariance time evolution equation and not in the state time evolution equation. This is because Gaussian numbers have a mean of zero. Just something to think about.

Alright, that is enough writing down of random equations. Read up on how they work in one of the many references and you will become a better person for it, if not a little more antisocial.

A 'Simple' Example

For a 'simple' one dimensional example, we would like to use the following equations,

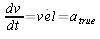(8)

and

(9).

Weirdly, and sadly for us, the true acceleration is not a known quantity so equations (8) and (9) are fiction. All we can do is estimate it. The position and velocity are also quantities that are estimated by the filter and are also never really known. So how do we estimate the acceleration? In this example we will model the true acceleration as

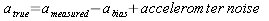(10).

First the accelerometer noise is observed by testing the accelerometer, how much does it vary in the output? Or how much do you trust the numbers that come out. Whichever one of those numbers is larger is the one to pick. Second we assume the accelerometer has a bias, and the Kalman Filter will estimate the bias then remove it from any measured acceleration.

There are other models of accelerometer errors, but they are more involved and the bias is one of the important error descriptions of an accelerometer. One other important type of error in inexpensive accelerometers is an overall scale factor. The scale factor would be another element of the state vector, if it were modeled. In this article it is not.

Last, the description of the position measurements is

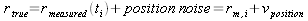(11).

I apologize that the noise variable looks just like the velocity, but it is common practice to use the same letter for both. The position noise is given by how accurate you think the position measurements are. Are they good to 1cm? 1mm? 5 ft? Use your brain, be honest, and take a guess. The smaller you make it the more important the filter will think the position measurements are, and if they are not that good your filter will give bad results.

Now we convert these equations to the form of equations (1) and (2). The state vector is defined

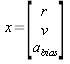(12).

In equation (12) the v really is the velocity. From this definition of the state vector we deduce the rest of the matrices in equation (1).

, ,

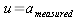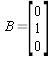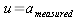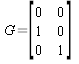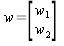, , , and (13).

In the F matrix the bias is assumed constant, i.e. its derivative is zero (This is noticeable in the F matrix also). The particular values we use for the w vector will depend on the accuracy of accelerometer and how fast we want the filter to respond and estimate the accelerometer bias. If you multiply these out, this will seem a lot less magical if you do not. If you multiply them out you correctly you will get equations (8) - (10) and the time evolution relationship between those equations. For the position element of the state vector, the time evolution equation, equation (3), multiplies out as 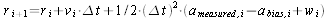This equation should make sense. If you multiply out the time propagation equations for the covariance matrix the results are less intuitive, but the outcome is the elements only get larger as time goes on. It takes a measurement to shrink the covariance. For equation (2) we get

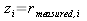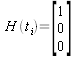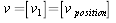, and (14).

(The v's in equation (14) are the noises from equation (2), not the velocity) The i represents the i-th measurement of the position, there will be many. The value of the position measurement noise will be determined from the accuracy of the position measurements, and I will assume the value of .5 cm, which is not horrible but not great. The real Wiimote can probably do better but this is a conservative preliminary guess.

A nice feature of this particular model is that most of the matrices and vectors are time independent so the equations can be computed beforehand, avoiding several matrix multiplies and the numerical integration of the matrices. This improves the speed and accuracy of the filter.

The last thing to do is to set up initial values for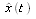and P(t), things that we probably do not know. A good way to start the state estimate is to set all the states to zero unless there is otherwise a good reason to set it differently. One good reason to set a state vector element to a nonzero value would be if the initial value is approximately known from a preliminary high quality measurement. For example if a position measurement is available, then that might be a good value to set as the initial position. A basic way to define the covariance matrix, P(t), is to set the off diagonal elements as zero and the diagonal elements as the large enough value to accept new measurements but not too large, otherwise the time for the filter to figure out good estimates for everything will take longer. This is one of the many balancing acts of Kalman Filter design.

Description and Evaluation of an Example with Fiducial Accelerometer Inputs

The test case that I executed involves imitating an accelerometer sitting still on a table. The accelerometer is motionless, but the accelerometers still have nonzero inputs. This is a good way to estimate the accelerometer biases. In order to get a player to hold the Wiimote still for a short amount of time while receiving position updates is easy enough. Just make an excuse, have them choose the club with the pointer and make the player hold that pose for a half to one second. I assume there is a position measurement every 1/100 of a second and the noise parameters are as follows:. If you play with these values you can adjust how fast the filter estimates the accelerometer bias and what the spread is of the estimations. Adjusting these parameters for the specific purpose at hand is another balancing act of Kalman Filter design.

In a fiducial run of the filter with random spreads in the position and accelerometer inputs the time it takes to estimate the accelerometer bias is shown in Figure 1. Even though the filter in this run does not settle down to exactly the .25 m/s/s of the 'real' accelerometer bias, it does settle down to .28 m/s/s. An error of .03 m/s/s is much better than the original error of .25 m/s/s, an improvement of approximately 88%. Many of the runs will settle down to values closer than this, and some not but if they are kept track of over time then these can be statistically analyzed to further improve the bias estimate.

The best thing about all this is that once the bias is estimated for the accelerometer, the trajectory of the Wiimote is estimated much more accurately than without the use of a Kalman Filter, even without further position measurements. Position measurements for the Wiimote are best when it is pointed at the base station receiver, but for games that involve swinging the Wiimote the pointer is often not aimed at the TV, hence this will greatly improve the estimation of the Wiimote's movement.

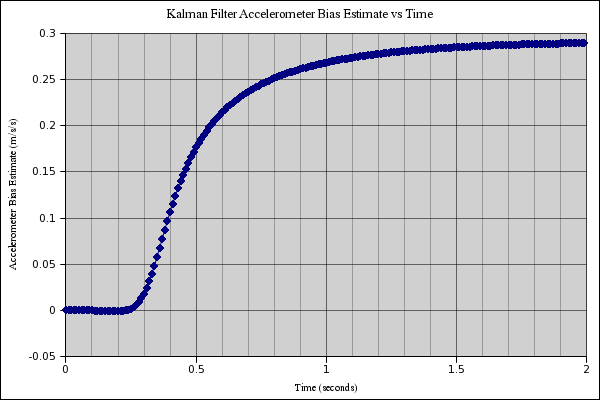
Figure 1. The estimate of the accelerometer bias as a function of time for a fiducial run. Note that the value it closes in on is not exactly the .25 m/s/s that is assumed in the test.

Issues with Kalman Filtering

Model issues

This is the difficult part of all of this, if you have a poor model things will not work well. If you have a poor model and know it, making the time propagation noise vectors larger can help a little. But for a filter to work well the model must represent reality accurately enough or the filter will end up saying strange things. And you do not get to blame the Kalman Filter, it is your own fault.

Memory and speed issues

Once models become complicated, the state vectors get big fast. Most navigation Kalman Filters have between 12 and 29 states. The trouble comes with the time propagation matrix, F(t), and with the matrix inversion in the equation (5). The measurement vectors also get bigger, but since most measurements are not larger than 3 dimensions this increase in size does not occur as fast.

The states on airplanes are not updated all that often, once every few seconds, since the airplane motion is in general smooth and accurately described by the time evolution equations. For something like the Wiimote the time between measurements is not as long so some worry about computation is justified.

Possible numerical issues

The Covariance matrix is supposed to be positive semi-definite. Basically this means that all of the eigenvalues should be 0 or greater. If the ratio of the eigenvalues of the matrix are greater than precision of the number type, then negative numbers can sometimes creep in. So if the largest eigenvalue is 10,000,000 and the smallest is 1.0 there will be trouble with making the various matrices out of floats.

For our example there is fairly little trouble with this but it is something to keep in mind if you set up a more complicated system and try to estimate small corrections to big numbers. Reference [4] has several elegant and impressive solutions to many numerical issues.

Conclusion

What was all of this complicated math for anyway? Well, the actual accelerometer outputs from the Wiimote are neither precise nor accurate. In order to use them as a better input, to simple sports games, sword fighting games, or any other game that allows the player to swing their arms around without always pointing the Wiimote at the base station and that requires accuracy to follow the Wiimote around. Once this is programming is done, the flexibility of the Wiimote as a unique input device will go well beyond its current capabilities.

Another potential use of Kalman Filter's is in AI. An example would be in a military game, it would be useful for the AI to estimate where it thinks the player is and how spread out his forces are. The mean and the covariance of the Kalman Filter give precisely this information. Much more appropriate and complicated models could be derived that would improve the AI's abilities.

References

[1] Maybeck, Peter S., Stochastic Models, Estimation, and Control Volume 1, Navtech Book & Software Store, 1994. Overall this reference is more formal mathematically than some of the other references, but the first chapter contains another 'simple' example and is a good place to start learning about Kalman Filtering.

[2] http://www.cs.unc.edu/~welch/kalman/ This is a nice site with many additional references. It focuses more on the computing aspects and less on the modeling aspects of Kalman Filter. Plus it has a picture of Mr. Kalman himself.

[3] Gelb, Arthur, Applied Optimal Estimation, M.I.T. Press, Cambridge, Massachusetts, 1974. This is a classic reference for engineers.

[4] Bierman, Gerald J., Factorization Methods for Discrete Sequential Estimation, Academic Press, New York, 1977. This is a reference that is full of optimized algorithms that tackle the many numerical issues involved in complex filters, even if they are in FORTRAN.

Code Samples

KalmanFilter.cpp
KalmanFilter.hpp
MainLoop.cpp

Note: These samples contain almost workable code. However, you will need your own vector classes, matrix classes, and file classes.

Acknowledgments

The author would like to thank Sam Denham, Ph.D. and Nathan Morse for their helpful comments in the preparation of this manuscript.