Using Bitmaps for Automatic Generation of Large-Scale Terrain Models

Players today demand a rich game experience with larger worlds to explore, more interesting things to do, and higher degrees of realism with each new title that ships. The problem is that game development schedules and budgets cannot keep pace with consumer demand for new feature sets. So, how do we make larger, more interesting worlds without blowing milestones and spending large sums of money? Simply put, we must have some of our game data generated automatically for us.

For example, suppose you're developing an online massively-multiplayer game with an enormous amount of polygonal terrain (hundreds of thousands of screens' worth of in-game scenes) for thousands of players to exist in and interact upon. In addition to that (just to make your life more difficult), this terrain model must conform to a loose, preexisting map specification (in other words, the general map layout and major landmark locations are known relative to each other, but there is no concrete data set describing the terrain, such as satellite imagery). This constraint eliminates the possibility of using any truly automatic terrain generation algorithm (such as fractal terrain generation). Meticulous construction of the terrain model by artists' hands is completely out of the question. No group of artists assigned this arduous task would be able to produce the desired result within the budget constraints; it will either cost a prohibitive amount of money, or take more time than is allotted for the development of the product. So you're left searching for some kind of middle ground between these two extremes.

Using manageably-sized, artist-generated bitmaps, combined with some clever image processing techniques, you can create a desirable terrain model. The techniques I describe in this article don't eliminate artist or world-builder involvement from the creation process - these techniques only create a model that is very close to completion in a relatively short amount of time. Once generated, the terrain must be fine tuned by an artist or level designer to add the aesthetically pleasing final touches.

There are several other advantages to using bitmaps for your terrain modeling. First and foremost, the tools for manipulating images (such as Photoshop) are extremely well developed and well known by a majority of artists. Second, the techniques I'm about to discuss will lower the ratio of time spent generating the terrain images to the amount of in-game data you can generate from them. Finally, this technique lets you view the layout of the entire world within a fairly small area - the bitmaps we will use are fairly manageable and allow you to view the entire image at once on a typical monitor.

It's assumed that the terrain model desired is a textured 3D polygonal mesh, with the vertices lying upon a regularly-spaced rectangular grid. The terrain's z-values (the "up" vector) are taken from a two-dimensional array of values called a height field. The terrain textures are also set according to a two-dimensional array of values, where different values denote specific types of terrain. This helps specify a texture to use for a particular cell in the terrain grid. Thus, two bitmaps are required to generate all the data needed to create terrain. In the examples provided in Figures 1a-b and 2a-b, the height and terrain data bitmaps are 8-bit grayscale and palletized color images, respectively.

Note that there are several methods by which you can use this terrain data to create a system of connecting tiles. For example, you could view each terrain value as an individual tile, or view each value as a tile vertex, and so on. However, this article is strictly concerned with generating the needed data. Showing you what to do with the data once it has been generated is beyond the scope of this article.

Bitmap Representation of Terrain and Elevation Data

Translating bitmap values into usable data is straightforward, assuming you can read the file format of the bitmap. For a given entry (x, y) in a height data bitmap, a corresponding value in the height field can be calculated by taking the value in the bitmap and multiplying it by some scalar: heightField (x, y) = bitmap (x, y) · scaleZ. Using the terrain bitmap is even easier. Since the bitmap is 8-bit, simply set the value (palette index) at any given point (x, y) in the image to a predetermined terrain type. If more than 256 terrain types are needed, you can use the RGB values of a 24-bit image for terrain type indexing instead.

While the goal is to use a large data set to generate a terrain model, it is unlikely that a 1:1 mapping of bitmap values to height and terrain values will yield a large enough data set for very large game worlds. Thus, you probably will have to "scale up" the bitmaps some way in order to generate sufficient amounts of data.

There are two easy ways to scale the data gathered from the height bitmap. The methods rely on a two-dimensional scale vector (scaleX, scaleY) to do the work. The scale vector is created based on the ratio of the size of the bitmap to the size of the terrain model one wishes to create from the bitmap.

The first method takes each pixel (x, y) in the height bitmap and duplicates the pixel value bitmap (x, y) inside a rectangular area of pixels scaleX · scaleY in size, in which the upper left corner of the rectangle equals (x · scaleX, y · scaleY). Empirically, the data becomes "pixellated," as though the bitmap is viewed at a higher zoom level. The terrain data is scaled in this way, as well.

The second method of scaling the height data treats the bitmap values as points on an arbitrarily large surface, or as control points used to generate such a surface parametrically, in which each value in the height bitmap is a discrete sample from this surface. For a given entry (x, y) in one's height-data bitmap, a corresponding value in the height field can be calculated using the following mapping function:

All we're doing is taking a point in the height data bitmap and multiplying it by a scale vector of (scaleX, scaleY, scaleZ).

Now that the amount of raw data needed to create the full size terrain model has been generated, one might notice (see Figures 1a-b, 2, and 3a) that scaling the bitmaps has created some rather harsh and unwanted artifacts in the final images. To correct these artifacts, let's use some basic filtering techniques from the field of image processing.

Basic Image Processing and Elevation Smoothing

Many image processing operations can be modeled as a linear system:

where f(x, y) and h(x, y) are the input and output images, respectively, and g(x, y) is the system's impulse response. To put it another way, g(x, y) is the operation upon f(x, y) that creates h(x, y). For such a system, the output h(x, y) is the convolution of f(x, y) with the impulse response g(x, y), defined in discrete terms, for an NxM image, as:

If f and h are images, convolution becomes the computation of weighted sums of the image pixels. This computation is performed using an arbitrarily-sized square table of values called a convolution mask. This computation is what performs the actual filtering.

One of the simplest filters is implemented by a local averaging operation where the value of each pixel is replaced by the average of all the values in its local neighborhood, as determined by the size of our convolution mask. For example, taking a 3x3 neighborhood about the pixel (i, j) yields:

If g[i, j] = 1/9 for every [i, j] in the convolution mask, the convolution operation reduces to a local averaging of the 3x3 grid of pixels centered on pixel [i, j]. Notice that for the 9 pixels involved in the operation, the sum of the weights is equal to 1 (9x1/9 = 1). When an NxN convolution mask is used as an averaging filter, the size of N controls the amount of filtering. As N becomes larger, the image noise is reduced, but you also lose more image detail. So there's a trade-off in choosing a particular size N, and choosing the size of your convolution mask will depend on the amount of filtering you need and level of detail your final image requires. An example of an average filter applied to a height field is shown in Figure 3b.

A Gaussian filter is similar to the averaging filter. In the Gaussian filter, the values in the mask are chosen according to the shape of a Gaussian function. For reference, a zero-mean Gaussian function in one dimension is:

where the Gaussian spread parameter determines the width of the Gaussian. For image processing, a two-dimensional zero-mean discrete Gaussian function,

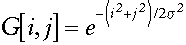
is used as a smoothing filter. The Gaussian filter has a few properties that make it particularly useful for smoothing purposes.

First, the Gaussian function is rotationally symmetric. In other words, the function does not favor any particular direction when it smooths, which is particularly useful when the areas needing smoothing are oriented in an arbitrary direction (not known in advance), and there is no reason to smooth in any specific direction.

Second, the Gaussian function has a single lobe, which means that the Gaussian filter replaces each pixel with a weighted average of the neighboring pixels around it (like the averaging filter), such that a pixel's weight decreases monotonically with distance from the central pixel.

The filter centers on one pixel (i, j). This pixel is modified by: 1) Multiplying each surrounding pixel, including the center pixel by its respective filter weight, and adding the resulting products together. 2) Dividing the sum from step one by the sum of the filter weights. This is the new value for pixel (i,j). This allows local features in the height bitmap to remain in the filtered image. Finally, the width (and thus the degree of smoothing) is linked directly to s, so that as s increases, so does the degree of smoothing. One can control this parameter to achieve a balance between the amount of smoothing and blurring in the final image.

There are a couple of techniques that one can employ to determine what kind of Gaussian filter to use. If the filter is being calculated directly from the discrete Gaussian distribution

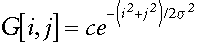
where c is a normalizing constant, the equation can be rewritten as

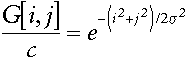
Once a value for s2 is chosen, the function can be evaluated over the NxN area desired for the mask. For example, choosing s = 2 and N = 7, the above equation yields the grid of values in Table 1. However, if integer values are desired inside the mask, you can divide every value inside the mask by the value at one of the corners in the array (the smallest value in the mask). With this completed, and assuming the values are rounded appropriately, a table is created like that shown in Table 2.

Notice that the sum of all the weights contained in the above Gaussian masks do not equal one. Thus, the result given from convolving a given section of the image by the mask should be divided by the sum of the weights contained in the mask. This ensures that the mask does not affect regions of uniform intensity. An example of the Gaussian filter shown above applied to a height field is seen in Figure 3c.

Another useful aspect of the Gaussian function is the fact that it is a separable function. In other words, a two-dimensional Gaussian convolution can be obtained by convolving the bitmap with a one-dimensional Gaussian and then convolving the result with the same one-dimensional Gaussian-oriented orthogonal to the Gaussian used in the first step. Therefore, another way to create a Gaussian filter is to approximate it by using the coefficients of the binomial expansion (you might remember the binomial series from calculus, where it was used to estimate integrals and roots of numbers):

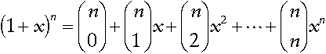
In other words, use row n from Pascal's triangle (Figure 4) as the values for your Gaussian filter. For example, a five-point approximation of a Gaussian filter is:

1 4 6 4 1

This corresponds to the fifth row in Pascal's triangle, as shown in Figure 4. This method works for filter sizes up to around n = 10. For larger filters, the binomial coefficients become too large for most images. Of course, if floating-point values can be used, you could always normalize the row by the largest value.

Depending on how much you scaled the original height bitmap, the above smoothing methods should produce satisfactory results. However, for higher amounts of scaling, the amount of smoothing needed (provided by either of the methods above) might be too high to produce a smooth height bitmap (depending on what kind of terrain model will be satisfactory). In doing so, there is a trade-off between losing local detail from the original height bitmap (since smoothing reduces noise by spreading it over a larger area, making it more difuse) and generating more terrain data from a bitmap of given size.

Smoothing Using Curved Surfaces

With images that have a large amount of height variation, such as a terrain that goes from a valley at sea level to a mountain peak, the amount of smoothing needed to produce a satisfactory terrain model would be so large that a great amount of detail would be lost in the process - your mountains might suddenly turn into rolling hills. So a different approach for these images must be used. A more obvious yet slightly more complicated method is to find some form of surface representation from the initial set of data points. This can be a surface either shaped by or interpolating through these points. There are many ways to do this, but this discussion will be limited to creating a uniform cubic B-spline surface to achieve our goal.

Introduction to B-Splines

I will assume that you have some basic knowledge of parametric curved surfaces, such as Bézier curves and surfaces. If not, Brian Sharp's articles on Bézier curves and surfaces ("Implementing Curved Surface Geometry," June 1999, and "Optimizing Curved Surface Geometry," July 1999) are a very good introduction.

You may recall that four control points define a cubic Bézier curve and that 16 control points define a cubic Bézier surface. In general, a degree n Bézier curve is defined by n + 1 control points, and a degree n Bézier surface is defined by

(n + 1)2. However, the desired final set of elevation points will be much larger than a 4x4 grid. Therefore, one will need to use either a much larger degree Bézier surface, or employ another approach that will remain a third degree surface that allows any number of points to define it.

This is where the cubic B-spline comes in. In simple terms, a B-spline of degree n can be thought of as a composite curve made up of several curve segments, each also of degree n, with each curve segment defined by n + 1 control points. In this case, each curve segment is a third degree curve defined by four control points. An important feature of the B-spline is what's known as "C2 continuity." This means that at any point on the curve, the second derivative will exist (means that no sharp points will exist anywhere on the curve - a nice property to have). To define the B-spline as a whole, if we have m + 1 control points, then we have m - 2 curve segments. Let a given curve segment Qi be defined over the interval 0 = u = 1 by basis functions Bk(u)(k = 0,…,3) and control points pi , pi+1, pi+2, pi+3 as follows:

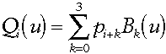
This should look familiar, since it's very reminiscent of how a Bézier curve is defined. For the sake of brevity, here are the basis functions for a cubic B-spline (if you'd like more information how the functions are actually derived, please see the References section at the end of this article):

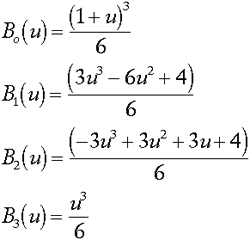
Since these segments are connected together to create one large curve, it makes sense to have a parameterization of the entire curve in terms of one parameter U, instead of having just a parameter u for every curve segment. Globally, U is defined over [0, m - 2], and u defined (as one would expect) over [0, 1]. The parameter u for any given curve segment i is given by U - i.

Except for the end points of the B-spline curve, each control point (in the case of a cubic B-spline) influences four curve segments, that is, control point pi influences curve segments Qi -3, Qi -2, Qi -1, and Qi. The influence of each control point pi over the curve at some global parameter value U is "collected" into one global function (called a blending function), Ni(U).

Think of the blending function as the sum of the basis functions (which is similar to the basis functions used when evaluating Bézier curves) for any given point on the curve. In formal terms, the B-spline curve Q(U) is defined by:

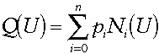
where

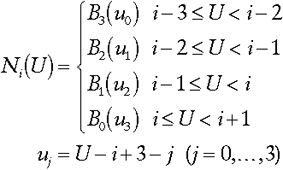
The global function Ni(U) takes the global parameter U and converts it to the appropriate local parameter uj for each curve segment involved.

As mentioned earlier, this type of B-spline is a uniform B-spline, which means that the curve consists of curve segments between endpoints that are spaced equally apart (there are other types of B-splines that do not have the ends equally spaced, but we won't worry about those here, since we're dealing with a regular grid of control points). In our case, these ends are located at [0, 1, …, m] of U for m number of control points. These ends will be referred to as knots (to be consistent with any other reference one may find on B-splines). Thus, the spline curve becomes a collection of the knot intervals t0 < t1 < ··· < tm. Also, the order k (the degree + 1) of a B-spline can vary, but for simplicity's sake, we will keep the order of our spline constant at k = 3. Now we can recursively define a blending function Ni,k(u) of degree k over the knot range [ti, ti + k] as follows (otherwise known as the Cox de Boor algorithm):

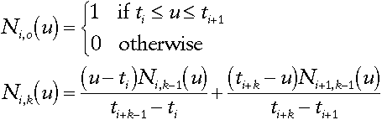
Now that we have the definition of a B-spline curve, how do we define a B-spline surface? Informally put, any point (u, v) on the surface is calculated by multiplying two separate curves together. Formally, let a point (u, v) on a cubic

B-spline surface S defined by a grid of control points

pi,j(i = 0, … , n; j = 0, … , m), and blending functions Ni,k(u) and Mj,k(v)

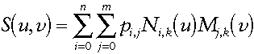
Now that we have basic knowledge of B-splines, applying what we have learned to create our desired amount of elevation data should be relatively easy. The initial set of elevation points should be used as control points for the final surface. Next, determine the dimensions the final elevation data should satisfy. Let our final elevation data set be s values wide by t values tall. When evaluating points on the surface, one needs to know the change in u(du) and change in v(dv) from one point to the next, which is defined by:

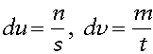
The code to do all of this is available on the Game Developer web site, http://www.gdmag.com.

Terrain Smoothing

In smoothing the terrain bitmap, neither the straightforward smoothing algorithms described above nor any other image processing technique used for scaling or smoothing images can be applied. All of these methods have potential to introduce new color values into the final image, and only the terrain values contained in the original terrain bitmap can be present in the final bitmap. In this smoothing method, another nxn array of values centered on a pixel g[i, j] in an image g will be used to calculate the value of the pixel h[i, j] in the final image h. However, instead of using an equation or other means independent of the values contained in the source bitmap, the values in the nxn convolution mask will be taken directly from source bitmap (specifically, the nxn neighborhood surrounding pixel g[i, j]). Next, a histogram (an "inventory" of all the different values contained in the specific nxn area of the source bitmap) of the nxn array is calculated. From this histogram, the value that is most frequently occurring in the nxn region surrounding the pixel g[i, j] shall be the value of the pixel h[i, j].

Conclusion

The convenience of using bitmaps for generating game data can extend beyond just polygonal terrain generation. Other examples could be world object placement (for trees and other vegetation), non-player character (NPC) placement (perhaps for a real-time strategy game where hundreds of units need to be placed for a given scenario), setting paths for NPCs to follow, or providing any addition information about the terrain (for example, setting "off-limits" areas for certain player characters or NPCs). The number of things that an image can represent is virtually limitless. So, before considering creating your own custom tools for generating game data, make sure that you're not simply reinventing the wheel by wanting to provide something that a bitmap could provide just as well.

References

Image Filtering

Gonzalez, Rafael C., Richard E. Woods, and Ralph Gonzalez. Digital Image Processing. New York: Addison-Wesley, 1992.

Jain, Ramesh, and others. Machine Vision. New York: McGraw-Hill College Division, 1995.

Curved Surfaces and Surface Interpolation

Rogers, David F. Mathematical Elements for Computer Graphics. New York: McGraw-Hill College Division, 1989.

Watt, Alan and Mark Watt. Advanced Animation and Rendering Techniques: Theory and Practice. New York: Addison-Wesley, 1992.