Subdivision Surface Theory

At Siggraph '98, Pixar unveiled a short animated film. Christened Geri’s Game, it was, to quote its Academy Award press release, the “endearing tale of an aging codger who likes to play chess in the park against himself.” Not only was it artistically stunning, but it was also a technological powerhouse. The short served as a vehicle to demonstrate Pixar’s latest addition to its production environment, a surface scheme known as subdivision surfaces.

Subdivision surfaces are a way to describe a surface using a polygonal model. Like the polygonal model, the surface can be of any shape or size — it’s not limited to a rectangular patch. Unlike that polygonal model, the surface itself is perfectly smooth. Subdivision surface schemes allow you to take the original polygonal model and produce an approximation of the surface by adding vertices and subdividing existing polygons. The approximation can be as coarse or as detailed as your needs allow. Because Pixar’s rendering system requires everything to be broken into polygons that are a half-pixel across, subdivision surfaces allowed them to tessellate automatically to that level everywhere. As such, the artists didn’t need to worry about how close Geri was to the camera. While your game probably can’t quite deal with half-pixel polygons, whatever size you do choose, your models can scale up and down in polygon count with the speed of the machine and their distance from the camera.

The technology itself is, for the most part, not new, but its application up until recently has been fairly limited. Indeed, Geri’s Game is still one of the only compelling demonstrations of subdivision surfaces. Nonetheless, it brought attention to subdivision surfaces as a relatively new, up-and-coming technique for implementing scalable geometry.

Along with Pixar’s work, quite a few researchers are actively tackling issues in the area of subdivision surfaces, and several Siggraph papers each year advance them academically and put them to use in solving problems. By now, they are a fairly mature technology, and a compelling contender among scalability solutions.

The game development community realizes that scalable geometry techniques are an important part of developing next-generation game engines. The spread between high-end and low-end hardware seems to get bigger each year (thanks to current and forthcoming geometry accelerators such as Nvidia’s GeForce 256 and S3’s Savage2000), forcing game developers to find ways to cater to the masses that use low-end machines while building in features that make the most of hardcore gamers’ advanced hardware. As a result, on the low end our engines should still be capable of using fewer than 10,000 polygons per scene, but on the high end, the sky’s the limit: even hundreds of thousands of polygons per scene can cruise along at 60 frames per second. Scalable geometry techniques such as subdivision surfaces are therefore necessary to accommodate this variation in hardware capabilities.

In this article, a number of different kinds of subdivision surfaces will be discussed. As a preliminary warning, this article is entirely theory. Next month, we’ll look at an example implementation of one of the schemes, the modified butterfly, which I’ll discuss here. Keep in mind as you read this article that not every concept described here will be practical for use in your engine. Indeed, some subdivision surface models may not be feasible for use in games at all. But knowing the strengths and weaknesses of the various models will help you make the right decision for your next game.

The What and the Why

First, what is a subdivision surface? The obvious answer is that it’s a surface generated through subdivision. To elaborate, every subdivision surface starts with an original polygonal surface, called a control net. Then the surface is subdivided into additional polygons and all the vertices are moved according to some set of rules. The rules for moving the vertices are different from scheme to scheme, and it is these rules that determine the properties of the surface. The rules of most schemes (including all the ones discussed here) involve keeping the old vertices around, optionally moving them, and introducing new vertices. There are schemes that remove the old vertices at each step, but they’re in the definite minority.

The one thing the control net and the eventual surface (called the limit surface) have in common is that they are topologically the same. Topology is a way of describing the structure of a surface that isn’t changed by an elastic deformation, that is, a stretching or twisting. A good example and common joke is that to a topologist, a coffee cup and a donut are identical. The donut hole corresponds to the hole in the handle of the coffee mug. On the other hand, a sphere and coffee mug are not topologically equivalent, since no amount of stretching and twisting can punch a hole in that sphere.

Topology is one reason that subdivision surfaces are worth a look. With Bézier or B-spline patches, modeling complex surfaces amounts to trying to cover them with pieces of rectangular cloth. It’s not easy, and often not possible if you don’t make some of the patch edges degenerate (yielding triangular patches). Furthermore, trying to animate that object can make continuity very difficult, and if you’re not very careful, your model will show creases and artifacts near patch seams.

That’s where subdivision surfaces come in. You can make a subdivision surface out of any arbitrary (preferably closed) mesh, which means that subdivision surfaces can consist of arbitrary topology. On top of that, since the mesh produces a single surface, you can animate the control net without worrying about seams or other continuity issues.

As far as actual uses in games, I believe that subdivision surfaces are an ideal solution for character modeling. Environments and other parts of a game generally don’t have the fine detail or strange topology that would require subdivision surfaces, but characters can have joint areas that are particularly hard to model with patches, and characters are in constant animation, which makes maintaining continuity conditions very important.

The basics. Before we start discussing individual schemes, let’s look at the basic characteristics of subdivision surfaces in general. This gives us a framework for classifying and comparing the schemes as we come across them. Most of these characteristics carry notable implications with them, whether they are implied computational costs or implied ease-of-use considerations, or anything else. These will usually be the criteria on which you might choose one scheme above another.

Continuity: the holy grail. The first characteristic of a scheme is its continuity. Schemes are referred to as having Cⁿ continuity, where n determines how many derivatives are continuous. So if a surface is C⁰ continuous, it means that no derivatives are continuous, that the surface itself doesn’t have open holes. If a surface is C¹ continuous, it means that the surface is closed and that its tangents are continuous (so there aren’t any sharp seams).

This probably won’t be a major selling point of one scheme above another, since just about every scheme has C¹ continuity everywhere. Some have C² continuity in some places, but the majority have areas where the best they can claim is C¹. So most schemes are alike in this regard.

However, continuity is most certainly worth mentioning because it’s one of the major reasons to think about using subdivision surfaces in the first place. After all, Pixar could have modeled Geri using as many polygons as they wanted, since they’re not running their movies in real time. But no matter how many polygons they used, you could get close enough that Geri’s skin would look faceted from the polygons. The point of using a subdivision model is that you have that ideal limit surface at which you can always throw more and more polygons as you get closer and closer to, no matter how high the display resolution or how close the model is to the screen. Only a very small portion of the real world is flat with sharp edges. For everything else, there’s subdivision surfaces.

To Interpolate or not to Interpolate...

While the degree of continuity is generally the same for all subdivision schemes, there are a number of characteristics that vary notably between schemes. One important aspect of a scheme is whether it is an approximating scheme or an interpolating scheme. If it’s an approximating scheme, it means that the vertices of the control net don’t lie on the surface itself. So, at each step of subdivision, the existing vertices in the control net are moved closer to the limit surface. The benefit of an approximating scheme is that the resulting surface tends to be very fair, having few undulations and ripples. Even if the control net is of very high frequency with sharp points, the scheme will tend to smooth it out, as the sharpest points move the furthest onto the limit surface. On the other hand, this can be to the approximating scheme’s detriment, too. It can be difficult to work with, as it’s harder to envision the end result while building a control net, and it may be hard to craft more undulating, rippling surfaces as the scheme fights to smooth them out.

If it’s an interpolating scheme, it means that the vertices of the control net actually lie on the limit surface. This means that at each recursive step, the existing vertices of the control net are not moved. The benefit of this is that it can be much more obvious from a control net what the limit surface will look like, since the control net vertices are all on the surface. However, it can sometimes be deceptively difficult to get an interpolating surface to look just the way you want, as the surface can develop unsightly bulges in areas where it strains to interpolate the vertices and still maintain its continuity. Nonetheless, this is usually not a tremendous problem.

Figure 1 shows examples of an approximating scheme (on the left) and an interpolating scheme (on the right). The white outline is the control net, and the red wireframe is the resulting surface after a few subdivision steps. You can see the difference quite clearly: the approximating surface seems to pull away from the net, while the interpolating surface flows through the vertices of the net.

Surfaces in Uniform

Another set of characteristics of a scheme brings in four more terms. A scheme can be either uniform or nonuniform, and it can be either stationary or nonstationary. These terms describe how the rules of the scheme are applied to the surface. If the scheme is uniform, it means that all areas of a control net are subdivided using the same set of rules, whereas a nonuniform scheme might subdivide one edge one way and another edge another way. If a scheme is stationary, it means that the same set of rules is used to subdivide the net at each step. A nonstationary scheme, on the other hand, might first subdivide the net one way, and then the next time around use a different set of rules.

All the schemes we’ll talk about here are fundamentally both uniform and stationary. There are some extensions to these schemes that make them nonstationary or nonuniform, but there aren’t many subdivision schemes that are fundamentally nonstationary or nonuniform. One of the main reasons for this is that most of the mathematical tools we have for analyzing schemes are unable to deal with dynamically changing rules sets.

Subdivision Shape

Another characteristic of a scheme, albeit less significant than the prior ones, is whether it is triangular or quadrilateral. As the names would imply, a triangular scheme operates on triangular control nets, and a quadrilateral scheme operates on quadrilateral nets. Clearly, it would be inconvenient if you had to restrict yourself to these primitives when building models. Therefore, most quadrilateral schemes (including the one discussed here) have rules for subdividing n-sided polygons. For triangular schemes, you generally need to split the polygons into triangles before handing them over to be subdivided. This is easy enough to do, but one downside is that for some schemes, the way you break your polygons into triangles can change the limit surface. The changes are usually minor, though, so you simply need to be consistent: if you randomly choose which diagonal of a quadrilateral to split on every frame, you’ll end up with popping artifacts.

Figure 2 shows examples of a triangular subdivision scheme as compared to a quadrilateral scheme. Notice that the triangular scheme only adds new vertices along the edges, whereas the quadrilateral scheme needs to add a vertex in the center of each face. This is one reason why triangular schemes tend to be somewhat easier to understand: their rules have that one fewer step in them.

Extraordinary Vertices

The preferred vertex valence is another property of subdivision schemes. The valence of a vertex is the number of edges coming out of it. Most every vertex a scheme produces during subdivision has the same valence. Vertices of that valence are the regular vertices of a scheme. Vertices of any other valence are known as extraordinary vertices. Their effect depends on the subdivision scheme, but historically there have been problems analyzing the limit surface near extraordinary vertices. As we look at various schemes, we’ll see the effect that extraordinary vertices have on each one.

Most schemes don’t ever produce extraordinary vertices during subdivision, so the number of extraordinary vertices is set by the original control net and never changes. Figure 3 is an example of two steps of a triangular scheme with an extraordinary vertex in the center. Notice how it remains the only extraordinary vertex after a step of subdivision. Also note that the valence of the regular vertices is 6. This is common for triangular schemes, as they all tend to split the triangles in the same way — by adding new vertices along the edges and breaking each triangle into four smaller triangles.

Surface Evaluation

Surface evaluation is the process of taking a control net, adding vertices, and breaking faces into more, smaller faces to find a better polygonal approximation of the limit surface. There are a number of ways to evaluate a subdivision surface. All subdivision schemes can be evaluated recursively. Furthermore, most (including all the ones discussed here) can be explicitly evaluated at the vertex points of the control net. For interpolating schemes, this means that you can explicitly calculate the surface normals at the vertices using what are called tangent masks. For approximating schemes it means you can also explicitly calculate the vertex’s limit position, using what are called evaluation masks. In this context, a mask isn’t the same kind of mask that you might use during binary arithmetic. Our masks are more analogous to the masks worn at a masquerade. They are like stencil cutouts, shapes that can be “placed” on the control net, and their shape determines which of the surrounding vertices are taken into account (and how much effect each has) in determining the end result, be it the vertex location or its tangent vectors. Figure 4 shows a visual example of applying a mask to a surface at a vertex.

An important aspect of evaluation is the scheme’s support. The support refers to the size of the region considered during evaluation. A scheme is said to have compact support if it doesn’t have to look very far from the evaluation point. Compact support is generally desirable because it means that changes to a surface are local — they don’t affect the surface farther away.

A Note on Notation

Since the original authors of many subdivision schemes weren’t operating in concert with one another, the notation used between schemes tends to vary fairly wildly. Here, I’ve tried to stick with a fairly consistent notation. When talking about a specific vertex, it is v. If it matters what level of recursion it’s at, that level i is indicated as a superscript, so the vertex is vⁱ. The vertex’s valence is N. The neighboring vertices of the vertex are e_j where j is in the range [0,N–1]. Again, if the level of recursion matters, that level i is a superscript, so eⁱ_j is the jth edge vertex at level i. I try to use this notation everywhere, but there are a few places where it’s much clearer to use a different notation.

The one problem with a standard notation is that if you access some of the references at the end of this article, they will very likely use their own, different notation. As long as the concepts make sense, though, it shouldn’t be difficult to figure out someone else’s naming convention.

The Polyhedral Scheme

The polyhedral scheme is about the simplest subdivision scheme of all, which makes it a good didactic tool but not the kind of scheme you’d ever actually want to use. It’s a triangular scheme where you subdivide by adding new vertices along the midpoints of each edge, and then break each existing triangle into four triangles using the new edge vertices. A simple example is shown in Figure 5. The problem with this, of course, is that it doesn’t produce smooth surfaces. It doesn’t even change the shape of the control net at all. But it serves to demonstrate some concepts fairly well.

The scheme is clearly interpolating since it doesn’t move the vertices once they’re created. It’s also triangular, since it operates on a triangular mesh. Furthermore, the scheme is uniform since the edge’s location doesn’t affect the rules used to subdivide it, and stationary since the same midpoint subdivision is used over and over. The surface is only C0 continuous, since along the edges of polygons it doesn’t have a well-defined tangent plane. The regular vertices of this scheme are of valence 6, as that’s the valence of new vertices created by the scheme. However, this scheme is simple enough that it doesn’t suffer because of its extraordinary vertices.

The evaluation of the scheme isn’t hard at all. You can evaluate it recursively using the subdivision rules. As far as evaluation and tangent masks go, it’s clear that we don’t need an evaluation mask, since the points are already on the limit surface. Tangent masks don’t really make any sense, since our surface isn’t smooth and therefore doesn’t have well-defined tangents everywhere.

Figure 6 shows a tetrahedron control net in white with a red wireframe of the surface after a few subdivision steps of the polyhedral scheme.

Float Like a Butterfly...

The next scheme is known as the butterfly subdivision scheme, or, in its current form, the modified butterfly scheme. It shares some similarities with the polyhedral scheme, but has some differences, notably that it’s C¹ continuous and therefore actually produces a smooth surface.

The butterfly scheme has a fairly interesting history to it. In 1990, Dyn, Levin, and Gregory published a paper titled “A Butterfly Subdivision Scheme for Surface Interpolation with Tension Control” (see For Further Info at the end of this article). It described the first butterfly scheme. The title is derived from the stencil, or map of neighbors used during evaluation, which is shaped like a butterfly (Figure 7). The scheme is interpolating and triangular, so all it ever does is add vertices along the edges of existing triangles. The rules for adding those vertices are simple, and the support is compact. For each edge, sum up the vertices in the stencil-shaped area around that edge, weighting each one by a predetermined weight. The result is the new vertex. The weights used, corresponding to the vertex labelings in Figure 7, are these:

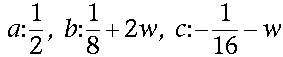
In this case, w is a tension parameter, which controls how “tightly” the limit surface is pulled towards the control net — note that if w equals –1/16, the scheme simply linearly interpolates the endpoints and the surface isn’t smooth.

One question that the scheme doesn’t answer, though, is what to do if the area around an edge doesn’t look like that butterfly stencil. Specifically, if either of the edges’ endpoints is of a valence less than 5, there isn’t sufficient information to use the scheme, leaving you with no choice but to choose w = –1/16 near that area, resulting in a surface that isn’t smooth near those extraordinary points. This means that while the surface is smooth almost everywhere, there will be isolated jagged points that really stand out visually and make the surface harder for an artist to craft.

In 1993, Dyn and his colleagues extended the butterfly scheme to use a ten-point stencil, so that the default case was the one shown in Figure 8, similar to the eight-point case with the rear vertices added in. The new weights are:

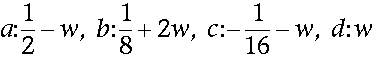
Note that by adding w to the d points and subtracting it from the a points, the stencil’s total weighting still adds up to 1. Intuitively, this is important because it means that the new point will be in the neighborhood of the ones used to generate it. If the weights summed to, say, 2, then the point would be twice as far from the origin as the points used to generate it, which would be undesirable.

This new scheme even reduces to the old scheme as a subset — choosing w = 0 results in the same rule set as the eight-point butterfly stencil. However, this extension didn’t address the smoothness problem at extraordinary vertices.

In 1996, Zorin, Schröder, and Sweldens published an extension of the butterfly scheme known as the modified butterfly scheme. The primary intent of their extension was to develop rules to use for extraordinary vertices, making the surface C¹ continuous everywhere.

If both of the endpoints of the edge are regular valence-6 vertices, the scheme uses the standard butterfly’s ten-point stencil with the same weights.

If only one of the endpoints is extraordinary, the new vertex is computed by the weighted sum of the extraordinary vertex and its neighbors (see the stencil in Figure 9). Note that you actually do not consider some of the neighbors of the regular vertex in doing this, which might seem a little odd. Given the extraordinary vertex’s valence of N, the weights used are:

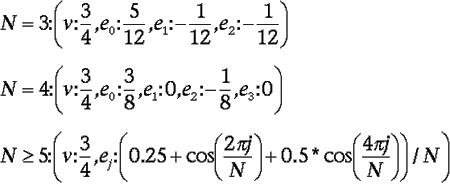
The full justification for these weights is available in Zorin’s thesis (see For Further Info at the end of this aritcle).

If both endpoints of the edge are extraordinary, the vertex is computed by averaging the results produced by each of the endpoints. So, evaluate the vertex once for each endpoint using the appropriate weights from above, and average the resulting two candidates.

Those, then, are the rules for recursively evaluating the surface. Since the scheme is interpolating, you don’t need an evaluation mask, but it would be nice to have a tangent mask to explicitly find the tangents at vertices. Such a mask exists, although it’s fairly lengthy to write out, and not particularly enlightening. It can be found in Zorin’s thesis, and I’ll discuss it next month when implementing this scheme.

Figure 10 shows a tetrahedron control net in white with a red wireframe of the surface after a few subdivision steps of the modified butterfly scheme.

Catmull-Clark Surfaces

The final scheme we’ll examine has some significant differences from the modified butterfly. Notably, it’s quadrilateral and it’s approximating, and so presents some new challenges. Its regular vertices are of valence 4, since a regular quadrilateral surface is a rectangular grid with vertices of valence 4.

Because this scheme is quadrilateral, it has to deal with things like placing vertices in the centers of polygons, and the rules are generally a bit more complex. Vertex addition is done in three steps. For each face in the old control net, add a vertex in its center, where the center is found by averaging its vertices. Then, for each edge in the old control net, a new vertex is added equal to the average of the edge’s endpoints and the new adjacent face points (see Figure 11 for an illustration).

Finally, move the original vertices of the old control net using neighboring points in the calculation. The stencil is shown in Figure 12; the rules are as follows:

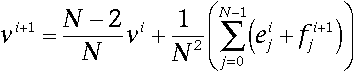
New edges are then formed by connecting each new face point to its adjacent new edge points and connecting each new vertex point to its adjacent new edge points. This defines the faces as well, and it brings up an interesting point: consider what happens when you subdivide a surface with a polygon that is not a quadrilateral. The resulting new face vertex will be connected to k new edge vertices, and k will not be equal to four. Therefore, the new face vertex is an extraordinary vertex. This is the only one of the three schemes shown here where the scheme can actually create an extraordinary vertex during subdivision.

This is not as bad as it may seem, though. After a single subdivision step, all the faces in the control net are quadrilaterals. Therefore, the scheme can only introduce new extraordinary vertices during the first subdivision step. After a single subdivision step, the number of extraordinary vertices is set and will not change.

The scheme also has evaluation and tangent masks for evaluation at the vertices. The full discussion and proof of the evaluation mask can be found in Halstead et al. and is fairly lengthy. The mask itself is fairly simple, though. For a vertex of valence N, the mask is equal to:

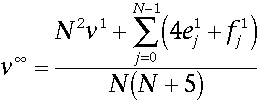
It’s interesting to note that this mask requires that we’ve subdivided the net once, since it uses the face and edge vertices of the same level as the corner vertices, and face and edge vertices are not available in the original control net.

The tangent masks carry an equally lengthy discussion, but their resulting formula is also fairly complicated. Because most of it can be precomputed for each valence and stored in a lookup table, it’s not computationally expensive, it’s just a large formula:

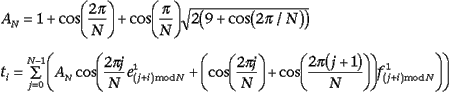
The surface normal is then the normalized cross product of t₀ and t₁.

Figure 13 shows a tetrahedron control net in white with a red wireframe of the surface after a few subdivision steps of the Catmull-Clark scheme.

Catmull-Clark Extended

Catmull-Clark surfaces hold the distinction of being the favored surfaces for use in high-end rendering; they were the model employed by Pixar in Geri’s Game. Their mathematical elegance and the amount of work devoted to them make them a fairly attractive choice. For instance, work has been done on generating Catmull-Clark surfaces that interpolate a set of points, which, as an approximating scheme, they do not usually do. Furthermore, Pixar extended them for Geri’s Game to allow for sharp and semi-sharp creases in the surface.

Pixar’s scheme generating these creases is fairly straightforward. It allows an artist to specify for an edge or vertex that subdivision near that edge or vertex should be done sharply (using polyhedral subdivision) for some number of steps, from 0 to infinity. Intuitively, the more sharp steps that are used, the more creased the surface will appear near that edge. If the number is finite, then the surface will still be smooth, since eventually the surface will resume using the normal Catmull-Clark subdivision rules. If the crease is infinitely sharp, it isn’t smooth at all. Pixar put these to use on Geri’s skin features, adding creases to various locations across his body like between his skin and fingernails.

It’s worth noting that while this greatly extends the application of the surfaces, it changes the properties of the scheme. The scheme becomes both nonuniform, since different edges and vertices can be of differing degrees of sharpness, and nonstationary, because a semi-sharp crease is evaluated linearly for some number of steps and then smoothly for the rest. Near the creases, the surface no longer reduces to the B-spline surface, and it also invalidates the evaluation and tangent masks.

Geri’s Game clearly demonstrates the benefit of sharp and semi-sharp creases. However, for use in games, the evaluation and tangent masks are fairly important, and so it’s difficult to say whether the increased computational cost is worth the added functionality.

Are You Dizzy Yet?

After this whirlwind tour of subdivision surfaces, you might be feeling a little light-headed or dizzy. Hopefully though, you’ve picked up the concepts behind subdivision surfaces and maybe even thought of some good applications for them in projects you’re working on or getting ready to start. Since there’s nowhere near enough space to discuss implementation details for even just these three schemes, next month we’ll bear down and focus on one of them, the modified butterfly scheme. I’ll mention the reasons I think it’s a good choice for use in games, discuss some of the benefits and detriments, and then present an example implementation.

Until then, there’s certainly no dearth of information on subdivision surfaces. Much of it is available online. The ACM Digital Library is an excellent resource for this topic as much of the work in subdivision surfaces has been published in the recent Siggraph conferences. Furthermore, many of the papers, Siggraph or not, are available directly from authors’ web sites.

Acknowledgements

Thanks to Pixar for graciously allowing us to use images from their short animation, Geri’s Game. Thanks also to Denis Zorin for his suggestions and references, Jos Stam at Alias|Wavefront for his help and suggestions, and to Alias|Wavefront for allowing him to release his precomputed eigenstructures. Thanks to Chris Goodman of 3dfx for discussions, latté, and those hard-to-find papers, and to Adrian Perez of Carnegie-Mellon University for suggesting the subdivision scheme I eventually settled on.

For Further Info

• Catmull, E., and J. Clark. “Recursively Generated B-Spline Surfaces on Arbitrary Topological Meshes.” Computer Aided Design, 1978.

• DeRose, T., M. Kass, and T. Truong. “Subdivision Surfaces in Character Animation.” Siggraph ‘98. pp. 85–94.

• Dyn, N., J. A. Gregory, and D. A. Levin. “Butterfly Subdivision Scheme for Surface Interpolation with Tension Control.” ACM Transactions on Graphics. Vol. 9, No. 2 (April 1990): pp. 160–169.

• Dyn, N., S. Hed, and D. Levin. “Subdivision Schemes for Surface Interpolation.” Workshop in Computational Geometry (1993), A. C. et al., Ed.,” World Scientific, pp. 97–118.

• Halstead, M., M. Kass, and T. DeRose. “Efficient, Fair Interpolation Using Catmull-Clark Surfaces.” Siggraph ‘93. p. 35.

• Stollnitz, E., T. DeRose, and D. Salesin. Wavelets for Computer Graphics. San Francisco: Morgan-Kaufman, 1996.

• Zorin, D. “Stationary Subdivision and Multiresolution Surface Representations.” Ph.D. diss., California Institute of Technology, 1997. (Available at ftp://ftp.cs.caltech.edu/tr/cs-tr-97-32.ps.Z)

• Zorin, D., P. Schröder, and W. Sweldens. “Interpolating Subdivision for Meshes with Arbitrary Topology.” Siggraph ‘96. pp. 189–192.

ACM Digital Library
http://www.acm.org/dl

Joe Stam’s web site
http://reality.sgi.com/jstam_sea/index.html

Denis Zorin’s web site
http://www.mrl.nyu.edu/dzorin

Charles Loop’s web site
http://research.microsoft.com/~cloop

Siggraph ‘99 Subdivision Course Details, Notes, Slides
http://www.mrl.nyu.edu/dzorin/sig99

Geometric Modeling
http://muldoon.cipic.ucdavis.edu/CAGDNotes

When he's not sleeping through meetings or plotting to take over the world, Brian's busy furtively subdividing, hoping one day to develop his own well-defined tangent plane. Critique his continuity at [email protected].