Messing with Tangent Space

1. Assumptions

I will assume that you are familiar with some basic vector math and 3D coordinate systems. I will also use the left handed coordinate system (OpenGL uses the right handed system) throughout this document. For the pixel and vertex shaders I will assume that you understand the syntax of DirectX shaders. Many people seem to find assembly shaders quite intimidating. The main point of this article is to help you understand the concepts and not provide code. The code is provided only to assist you in understanding the concepts.

2. Introduction

In this article I will cover what tangent space is and how to convert a point between world space and tangent space. The main reason I wrote this article was so that a person new to pixel shaders will be able to quickly understand a fairly important concept and make his own implementations.

The second section was written to demonstrate a practical use of world space to tangent space conversion. That is when you will actually understand why tangent space is so important in many of today's pixel shaders. I am sure you will find many fancier tutorials for per-pixel lighting on the internet, but this one is meant to get you warmed up on tangent space.

That being said, lets get started...

3. Tangent space

1. What is tangent space

As far as the name goes, tangent space is also known as texture space in some cases.

Our 3D world can be split up in to many different coordinate systems. You already should be familiar with some of these – world space, object space, camera space. If you aren’t I think you are jumping the gun and would strongly recommend you go back to these topics first.

Tangent space is just another such coordinate system, with it’s own origin. This is the coordinate system in which the texture coordinates for a face are specified. The tangent space system will most likely vary for any two faces.

In this coordinate system visualize the X axis pointing in the direction in which the U value increases and the Y axis in the direction in which V value increases. In most texturing only U and V change across a face tangent space can be thought of a 2D coordinate system aligned to the plane of a face.

So what about the Z axis in tangent space?
The u and v values can be used to define a 2D space, but to do calculations in a 3D world we need a Z axis as well. The Z axis can be though of as the face normal, always perpendicular to the face itself.

For now we will call this n (for normal). The value of n will always stay constant at 0 across a face.

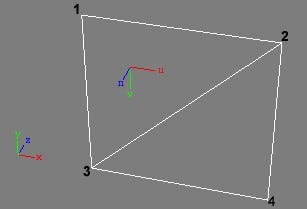
Figure 1: Tangent space axis for a face in a plane

Take a look at Figure 1. It will help you visualize the tangent space coordinate system. It shows a quad made up of four vertices and two faces assumed to have a simple texture unwrap applied to it.

Figure 2 shows the tangent space axis for a face on a cube defined by the vertices 1, 2, 3. Once again we assume that this cube has a very simple texture unwrap applied to it.
In the bottom left you will also see the axis for the world space coordinate system marked by x,y,z.

The u, v, n axis represent the direction in which u, v, n values increase across the face, just as the x, y, z values represent the direction in which the x, y, z values increase in the world space coordinate system.

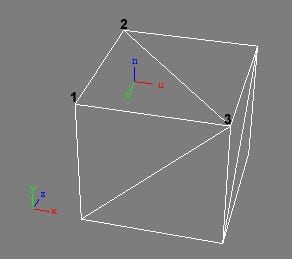
Figure 2: Tangent space axis for a face in a box

Let us take another example. In Figure 2 we try to visualize the tangent space for a top face of a box.

Why Use Tangent Space

Both, tangent space and world space represent a 3D space, just as inches and meters both represent length. If any meaningful calculations need to be done, all values must be in the same unit system or coordinate systems.

At this point you are probably wondering…

So why use tangent space in the first place? Why not just declare all positions and vectors in world space?

Certain per pixel lighting techniques and many other shaders require normals and other height information declared at each pixel point. This means that we have one normal vector at each texel and the n axis will vary for each texel. Think of it as a bumpy surface defined on a flat plane.

Now if these normals were declared in the world space coordinate system, we would have to rotate these normals every time the model is rotated even a small amount. Remember that the lights, camera and other objects also involved in these calculations will be defined in world space and will move independent of the object. This would mean thousands or even millions of object to world matrix transformations will need to take place at the pixel level. We all know matrix transformations don't come cheap.

Instead of doing this, we declare the thousands of surface normals in the tangent space coordinate system. Then we just need to transform the other objects (mostly consisting of lights, the camera, etc) to the same tangent space coordinate system and do our calculations there. The count of these objects won’t exceed 10 in most cases.
So it’s 1000000s vs 10s of calculations. Hmmm… It’s going to take a while to decide which one would be better.

Think of the box in figure 2 rotating. Even if we rotate it, the tangent space axis will remain aligned with respect to the face. Then instead of converting thousand or millions of surface normals to world space we convert tens or hundreds of light/camera/vertex positions to tangent space and do all our calculations in tangent space as required.

To add to the list of advantages of tangent space, the matrices required for the transformations can be pre calculated. They only need to be recalculated when the positions of the vertices change with respect to each other.

Hopefully you understand why we need tangent space and a transformation from world space to tangent space. If not, for now think of it as something that we just need to have and you will begin to understand when you read the second section.

3. Deriving a World space to Tangent space transformation matrix

In order to convert between coordinate system A to coordinate system B, we need to define the basis vectors for B with respect to A and use them in a matrix.

What are basis vectors?

Every n-dimensional coordinate system can be defined in terms of n basis vectors. A 3 dimensional coordinate system can be defined in terms of 3 basis vectors. A 2 dimensional coordinate system can be defined in terms of 2 basis vectors. The rule is that every vector that makes up a set of basis vectors is always perpendicular to the other basis vectors.

It’s basically one of those fancy mathematical terms given to three three vectors (in a 3D world) of unit size and perpendicular to each other. These three vectors can point in any direction as long as they are always perpendicular to each other. If you would like to visualize a set of basis vectors, think of an axis drawn in any 3D application. Look at Figure 1 & 2. The vectors that are on the axis (x, y, z) define one set of basis vectors. The vectors u, v, n also define another set.

Method of deriving world to tangent space transformation matrix

And why all the fuss over these basis vectors?
In order to achieve our goal, the first step is to define the u, v and n basis vectors in terms of the world space coordinate system. Once we do that, the rest is just a cakewalk.

From here on, I will refer to the u, v, n vectors as the Tangent (T), Bi-Normal(B) and Normal (N). Why? Because this is what they are actually called.

As I said before we need to find the T, B, N basis vectors with respect to world space. This is the first step in the process.

A simple way of thinking of this would be:
I have a vector that points in the direction in which the u value increases across a face, then what will be it’s value in the world space coordinate system.

Another way of thinking of it would be:
To find the rate of change of the u, v, n components across a face with respect to the x, y, z components of world space. The T vector is actually the rate of change of the u component with respect to world space.

Whatever way you choose to visualize it in, we will have the T, B, N vectors.
The next step is to build a matrix of the form:

Multiplying a world space position (Posws) with Mwt will give us the position of the same point in terms of tangent space (Posts)

As mentioned before the T, B, N vectors (and all basis vectors) will always be at right angles to each other. All we need to do is derive any two vectors and the third will be a cross product of the previous two. In most cases, the face normal will already be calculated. This means we just need one more vector to complete our matrix.

Creating the tangent space matrix for a face

In this section I will take a single face and then derive Mwt for the face.

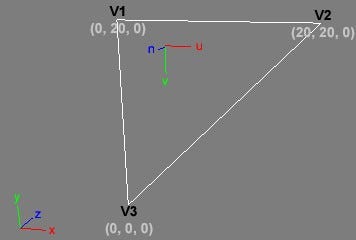
Figure 3: A sample face

Let’s assume the vertices of the face in Figure 3 have the following values

As stated in the previous section,

In order to derive T, B, N calculate the difference of the u, v, n components across the face with respect to the x, y, z components of world space.

Step 1: Calculate any two edge vectors. Edge

Step 2: Calculate the T vector

Step 3: Calculate the Normal vector (N)

Step 4: Calculate the Bi-Normal vector (B)

Step 5: Build Mwt from T, B, N

And volla! There we have our matrix.

Creating the tangent space matrix for a vertex

Ok, so you are all excited about your new magic matrix. But if you haven’t realized yet, there is no way we can send face data to the graphics card. When we draw a face on the screen, we create vertices in a certain order to define a face, but there is no real face data.
So we have one last step. Splitting up the transformation matrices that we generated for each face, to each vertex that defines the face. Some of you who have generated vertex normals will be familiar with some techniques to do this. You can use any of these methods for the T, B vectors just as you do for the N vector. For the rest I will describe a basic technique here. You can always use more complex methods if the need calls for it.

A fairly simple and common method is to calculate the average of the vectors from all the faces that share that vertex.
Example:
Taking the quad from Figure 1, lets say we have generated the Mwt matrix for the two faces. Lets call the two Mwt matrices M1wt for Face1,2,3 and M2wt for Face2,4,3.

In order to calculate T, B, N for vertex 1, we do as follows

We divide by 1 because V1 is used only by 1 face.

T, B, N values for vertex 2 are as follows

Here we divide by 2 because V2 is shared between 2 faces.
Note: that the T, B, N vectors need to be re-normalized after taking their average.

Putting everything together in pseudo code

I will put everything I discussed in the previous two sections together into some pseudo code. I’ve kept the pseudo code as close to C/C++ as possible, so the majority will find it easy to understand.

Declarations:

Data types:

Vector3, Vector2, Vertex, Face, Matrix3, Mesh

Vector3 =
{
Float X, Y, Z ;
}
Vector2 =
{
Float U, V ;
}
Vertex =
{
Vector3 P ;
Vector2 T ;
}

Face =
{
Integer A, B, C ;
}

Matrix3 =
{
Vector3 T, B, N ;
}
Mesh =
{
Vertex VertexList[] ;
Face FaceList[] ;
Matrix3 TSMarixList[] ;
}

Predefined Functions:

Pseudo Code:

TangentSpaceFace

Description: The TangentSpaceFace function calculates the tangent space matrix for a Face F and returns a 3X3 tangent space matrix for that face.
Note: In order to keep things simple, I have not taken care of special cases where the difference between two vertices will result in the u component being 0.

Matrix3 TangentSpaceFace(Face F, Vertex3 VertexList[])
{
Matrix3 ReturnValue ;

Vertex E21 = VertexList[F.B] - VertexList[F.A] ;
Vertex E31 = VertexList[F.C] - VertexList[F.A] ;

ReturnValue.N = Cross(E21.P, E31.P) ;
ReturnValue.N = Normalize(ReturnValue.N) ;

ReturnValue.T = E21.P / E21.T.u ;
ReturnValue.T = Normalize(ReturnValue.T) ;

ReturnValue.B = Cross(ReturnValue.T, ReturnValue.N) ;

return ReturnValue ;
}

TangentSpaceVertex
Description: This function calculates the tangent space matrix for a vertex with index position VertexIndex based on the list of faces that index this vertex from FaceList. FaceMatrix is an array of tangent space matrices for the face list passed in.

Matrix3 TangentSpaceVertex(Integer VertexIndex, Face FaceList[], Matrix3 FaceMatrix[])
{
Integer Count = 0 ;
Integer i = 0 ;
Matrix3 ReturnValue = ((0, 0, 0), (0, 0, 0), (0, 0, 0)) ;

ForEach ( Face in FaceList as CurrFace )
{
If(CurrFace.A == VertexIndex or CurrFace.B == VertexIndex or CurrFace.C == VertexIndex)
{
ReturnValue.T += FaceMatrix[i].T ;
ReturnValue.B += FaceMatrix[i].B ;
ReturnValue.N += FaceMatrix[i].N ;
++Count ;
}

++i ;
}

if (Count > 0)
{
ReturnValue.T = ReturnValue.T / Count ;
ReturnValue.B = ReturnValue.B / Count ;
ReturnValue.N = ReturnValue.N / Count ;

ReturnValue.T = Normalize(ReturnValue.T) ;
ReturnValue.B = Normalize(ReturnValue.B) ;
ReturnValue.N = Normalize(ReturnValue.N) ;
}

return ReturnValue ;
}

TangentSpaceMesh
Description: This calculates the tangent space matrices for the vertices in the Mesh M

TangentSpaceMesh(Mesh M)
{

Matrix3 FaceMatrix[M.FaceList.Count()] ;
Interger i ;

ForEach Face in M.FaceList as ThisFace
{
FaceMatrix[i] = TangentSpaceFace(ThisFace, M.VertexList) ;
}

For(i=0; i {
M.TSMarixList[i] = TangentSpaceVertex(i, M.FaceList, FaceMatrix) ;
}

}

4. Problems in practice

And it all comes crashing down…

So, that was all theory, but generally when you take something from theory and implement it in practice you end up with some problems. The same goes for the tangent space generation process.

Most problems arise from the way texture coordinates may be applied for an object during the texture unwrap stage. In most cases the artist would have done this to save on texture memory. The best solution is to him to fix the texture mapping at his end, rather than you write special cases for each object. In any case I have taken some commonly faces problems and explained how you can fix them. Most these solutions are less than perfect and should be avoided.

Upside down mapping

Take a look at Figure 4. It has two adjacent faces defined by the vertices 1,2,3 and 2,6,3 with inverted v channels. This will cause the lighting calculations in a per-pixel lighting shader to give wrong output.

This sort of a mapping would be an issue if all 3 vectors were generated only from the texture coordinates. If you plan to do this, the Normal vector will be inverted, since the Bi-Normal points in the opposite direction.

If you use the method explained above in this tutorial, this would be a non-issue and can be ignored completely.

Mirrored mapping

Ok, so we escaped solving problem one without any real problems. But what if the T vector was inverted, as would be the case in mirrored mapping?

Generate the Bi-Normal vector from the v channel first.
As we leaned from upside down mapping, our normal will be inverted. One simple way of doing this is to just avoid the inverted vector. Generate the Tangent vector from the cross product of the Normal and the Bi-Normal.

Another method listed by the guys at NVidia is to duplicate the edge sharing the inverted texture coordinates. Although this will work to create a valid world to tangent space matrix across a face, I don’t see how it will help as far as the lighting calculations go.

This fixes above would work if you had only one texture coordinate unit inverted, but what if your code needs to handle both an upside down mapping and mirrored mapping on two adjacent faces at the same time?
In this case, the only solution is to invert each of the vectors manually. Although I would consider this a dirty fix it looks like this is the only solution.

Detecting inverted texture coordinates between two adjacent faces can be fairly simple.

Once the Tangent and Bi-Normal vectors have been generated…

Cylindrical mapping

Another common problem that arises is with cylindrical mapping. In Figure 6 you can see a sample cylinder with cylindrical mapping applied on it. The second image is a close up of the same cylinder that shows the vertex edges where the two ends of the texture will meet. The u channel across the vertices on edge E1 will be 1.0 and the vertices on edge E2 will have a value of 0.0. This goes in the opposite direction of the rest the vertices on the cylinder. This would also cause the vectors of the tangent space matrix to be blended wrong across the faces between E1 and E2.

The solution here is to duplicate the vertices along edge E2 and attach them to the vertices on E1 to create new faces. They will have the exact same position as the old vertices. The old vertices on E2 will no longer be a part of the faces between E1 and E2. An important point to remember is that these vertices will be temporary. They will be used only to generate the world to tangent space matrix. They will not be used in the actual rendering, so the model and the texture on it will continue to look the same during rendering.

When generating the texture coordinates, you can assign fake texture coordinates to the temporary vertices. These fake coordinates should make sure that the Tangent vector will point in the same direction. In the above example, the temporary vertices along E2 could have a u value of 1.05 (Assuming the vertices on E1 have a u value of 1.0).
Another method would be use the same trick we used in mirrored mapping. We could generate the vectors from the v component and the face normals.

A third solution is to stretch the tangent space calculations between neighboring faces. In the above example, the faces between E1 and E2 would have their tangent space vectors calculated by stretching vectors from the left E1.

Spheres

Some time back I had a task to apply per pixel lighting shader on some pool balls. If you look at the way a sphere is modeled in Figure 7, you will realize that the vertices get closer to each other at the top and bottom until they finally join one single vertex. This would make the tangent space matrix completely wrong at the tip vertices as the tangent space vectors on the neighboring faces will nullify each other.

In this case your artist has just modeled the sphere wrong. You should go back and ask him to create the sphere as a geo-sphere as it is known in 3D Studio Max. Take a look at Figure 8. In a geo sphere the vertices will be spread evenly across the sphere and you should not have any problem generating the tangent space matrix.

4. Per-Pixel lighting using vertex and pixel shaders

In this section I will put all the boring mathematics discussed in the previous section to some real use.

I am assuming that you understand the basics of vertex and pixel shaders. I also assume you are familiar with the DirectX 9 API as I will make no attempt to explain functions from the D3D9 API here. Another point to remember is that I'm not going to try to teach you shaders here. The purpose of this section is to understand a practical use for all that was explained above.
Another assumption is that when I refer to a light I am referring to a point light.
I will only discuss calculating the diffuse component of a light to a surface here. There are several other calculations that need to be done in order for the lighting to look realistic. These would include attenuation, specular, and many other components. These are beyond the scope of this article and you can find several good articles covering these topics.

So what is per-pixel lighting

Previously lighting (color and brightness) was calculated at the vertex level and then interpolated across the surface of the face. This worked well if the model had an extremely high polygon count, but most games were required to keep the polygon count to a minimum in order to maximize their efficiency and in turn the FPS. In almost all cases teams went with vertex lighting only on player characters and the rest of the scene was lit statically via textures using lightmaps. Lightmaps work well, really well. You can have soft shadows, and very accurate lighting calculation, but one very serious drawback is that it works only if the objects are static at run-time. This is exactly the opposite of what a player expects in a game. A player expects everything to move and break (and a lot more than that too…). So most game design teams made a balance of dynamic objects to the non dynamic ones. The dynamic objects had a high poly count in many cases, so the vertex lighting on them worked well.

And then there was light…
And then when graphics cards became powerful enough, we found new ways [algorithms] to calculate light at every pixel. Now these are not entirely accurate, but as we know as long as it looks realistic enough, it works.

Most 3D APIs have vertex level lighting built into the API itself. But with per-pixel lighting we need to do it on our own. With per pixel lighting, every pixel point [texel] can have it’s own normal. Now we can have high resolution bumpy surfaces without worrying about the poly count of the object.

How light affects a surface and limitations in a traditional vertex lighting

Before we go to the actual calculations, lets quickly revise how a light affects a surface.

The diffuse component of how much a light affects a surface can be rounded off to the following equation.

Where

Take a look at Figure 9. It shows how the position of a light affects how brightly a surface is lit. L signifies the position of a light and N is the surface normal. We assume that the distance between the point and the light remain the same. As the light L makes an angle closer to 90^o, the surface becomes darker and darker.

Now the problem with traditional lighting is that the brightness with which a surface is lit is determined at the vertex level. If you look at the texture mapped face in Figure 9, you will see that even though the texture signifies bumps on the surface, the entire surface is uniformly lit regardless of the surface orientation at each texel. This means that the entire surface is dark or the entire surface is lit evenly. This will work fine only when the face makes up only a small part of the surface.

This is where per-pixel lighting comes in. In per-pixel lighting the brightness of the surface is determined at each texel instead of at each vertex, thus increasing the realism dramatically.

How bump mapping works

While doing bump mapping, in addition to the normal diffuse texture used, an additional texture called a normal map is used.

A normal map determines the orientation of the surface at each texel. Before we continue, don't be confuse a normal map with a height map or bump map as it is known in some 3D editing software such as 3D studio Max. Yes, a height map can be used for bump mapping, but it must be converted to a normal map before it can be used.

Now you may be a little confused as to how an image which holds RGB data encodes normals which have floating point x, y, z data. This is quite simple. A normalized vector always has 3 components x, y, z. The values of x, y, z always will range from -1.0 to 1.0. A 24-bit texture holds RGB values that range between 0 and 255. The x component of the vector is stored in the red channel, the y component in the green channel and the z component in blue channel. The x, y, z values are scaled and biased to a range between 0 to 255 before they are stored in the RGB values.

Example: Let us imagine we have a vector that identifies the normal at a point

Before we store Vn.x, Vn.y, Vn.z in the normal map as r, g, b data, we scale and bias the values as follows

The reverse of the above step is done in the pixel shader to get the surface normal from the normal map's RGB data. We then take the dot product of the surface normal at a point and the normalized light vector. Since the dot product of two unit/normalized vectors is equal to cos of the angle between them, no further calculations need to be done to get the brightness of a point at a texel.

Why does a normal map always look blueish?
The z component of a surface normal at point never points backwards

This results in

That is why you will always see a normal map having a blueish/purpleish tint. See Figure 10 for a sample height map and normal map. Note the difference between the two.

Another point to remember is that a normal map is always encoded in the tangent space coordinate system instead of the world space coordinate system. Go back to the section ‘Why use tangent space’ to understand why. You should get it now.

The vertex shader -calculating the light vector

The light vector is calculated at each vertex and then interpolated across the face. Although this is not an ideal method, there are some simple steps that we can follow at the game design level to prevent the disadvantages of using this method.

Step 1: Calculate the light vector.

In order to calculate the light vector, we assume that both the light position and the vertex position are in the world space coordinate system. The light vector is then calculated as follows

Where

Step 2: Convert the light vector from the world space coordinate system to a vector in the tangent space coordinate system.
Assuming that you have already calculated the tangent space matrix for each vertex and passed it into the vertex shader via the texture channels, this is just a simple matrix multiplication.

Step 3: Normalize the light vector

The light vector is then normalized.

This light vector is passed to the pixel shader in a previously decided texture stage. One very big advantage of doing this is that the light vector gets interpolated across the face for free.
Note: The interpolated light vector is no longer normalized when it reaches the pixel shader, but in our case this minor inaccuracy does not make any difference.

The pixel shader

Calculating the diffuse brightness at the pixel

Step 1: Get the light vector

Unlike getting a normal texture, you need to load the texture coordinate from the texture stage. This texture stage will generally not have any texture assigned to it. The light vector is cleverly stored as texture coordinates as a means of transporting data from the vertex shader to the pixel shader. This can be done using the texcrd instruction available in pixel shader 1.4.

There is no need to re-normalize the light vector at this stage. We can live with the inaccuracies and we will continue to assume that it is normalized.

Step 2: Get the normal at the texel

Assuming the normal map is assigned to a pre defined texture stage, load the normal / surface orientation at the texel and then scale and bias the values to fit back to a range from -1.0 to 1.0. If you remember, the values in RGB data range from 0 to 255 and when these are sent to the pixel shader they are converted to a range 0 to 1. The color data can be loaded using the texld instruction available in pixel shaders version 1.4

The first line loads the normal that is encoded as color data. The second line converts the color data back to a normal.

Step 3: Calculating the surface brightness

Now that we have the light vector and the surface normal at the texel, we can calculate the brightness of the surface at the using a simple dot3 product

As both the light vector and surface normal have already been normalized, the dot product will always range from a value from 0.0 to 1.0

Step 4: Modulate with the diffuse color

To get the color of the output pixel, just modulate [multiply] the color of the diffuse texture with the brightness at the current texel [pixel].

That is all that we need to do in order to get a bump mapped surface.

Putting it all together in vertex and pixel shaders

In this section I will put all the pseudo code discussed above into proper assembly shader code. I will be using vertex shaders 2.0 and pixel shaders 1.4. You can easily convert it to use any other version of your choice once you understand what is being done.

The vertex shader

vs.2.0
// c0 - c3 -> has the view * projection matrix
// c14 -> light position in world space

dcl_position v0 // Vertex position in world space
dcl_texcoord0 v2 // Stage 1 - diffuse texture coordinates
dcl_texcoord1 v3 // Stage 2 - normal map texture coordinates
dcl_tangent v4 // Tangent vector
dcl_binormal v5 // Binormal vector
dcl_normal v6 // Normal vector

// Transform vertex position to view
// space -> A must for all vertex shaders
m4x4 oPos, v0, c0
mov oT0.xy, v2

// Calculate the light vector
mov r1, c14
sub r3.xyz, r1, v0

// Convert the light vector to tangent space
m3x3 r1.xyz, r3, v4

// Normalize the light vector
nrm r3, r1

// Move data to the output registers
mov oT2.xyz, r3

The pixel shader

ps.1.4

def c6, -0.5f, -0.5f, 0.0f, 1.0f

texld r0, t0 // Stage 0 has the diffuse color

// I am assuming there are no special tex
// coords for the normal map.
// Stage 1 has the normal map
texld r1, t0

// This is actually the light vector calculated in
// the vertex shader and interpolated across the face
texcrd r2.xyz, t2

// Set r1 to the normal in the normal map
// Below, we are biasing and scaling the
// value from the normal map. See Step 2 in
// section 2.5. You can actually avoid this
// step, but i'm including it here to keep
// things simple
add_x2 r1, r1, c6.rrrr

// Now calculate the dot product and
// store the value in r3. Remember the
// dot product is the brightness at the texel
// so no further calculations need to be done
dp3_sat r3, r1, r2

// Modulate the surface brightness and diffuse
// texture color
mul r0.rgb, r0, r3

5. Conclusion

We have covered quite a bit in this article. You are finally at the end and hopefully the tangent space concept is clear to you.

Here are some tools and articles that will help you cover parts that this article has not and will help you take things further.