Implementing Subdivision Surface Theory

In my previous article "Subdivision Surface Theory", I explained what subdivision surfaces were and why game developers should be interested in them. I also covered a couple different kinds of subdivision surfaces in their mathematical forms and briefly discussed their benefits and detriments. Most everything was in English, and the rest was expressed using equations. There were no code listings last month, not even a hint of C++, but I promised to discuss an implementation, and so that's the goal of this article. I'll cover a sample implementation of the modified butterfly scheme as discussed in last month's article, complete with a shiny, new demo.

Why the Butterfly?

In "Subdivision Surface Theory" , I wrote about a number of schemes and those were only the tip of the iceberg, so it's worth spending some time justifying the choice I've made for this implementation. Why use the modified butterfly? To explain my reasoning, it helps to look at more general characteristics of schemes and their advantages and disadvantages. The major differences tend to hinge on whether a scheme is approximating or interpolating.

Approximating schemes have a number of benefits. The surfaces they produce are generally very fair, and they are generally the favored schemes for use in high-end animation. For instance, Pixar uses Catmull-Clark surfaces for their character animation. The downside of approximating schemes are substantial, though. The major one is that because the scheme doesn't interpolate its control net, the shape of the limit surface can be difficult to envision from looking at the control net. The caveat is that as the net becomes denser, the surface will generally be closer to the net. But for games, the net itself won't be tens of thousands of polygons, so the surface can differ substantially from the net.

Interpolating schemes are a different story. They can exhibit problems with fairness, with ripples and undulations over the surface, especially near tight joint areas. Also, they aren't used in high-end rendering quite as much, which can mean that they're the focus of less research. But their major benefit is that the surface is substantially easier to envision by looking at the net. Since the surface passes through all the net vertices, it won't "pull away" from the net. The fairness issues are the price to pay for this, though. Approximating schemes are fair because the surface isn't constrained to pass through the net vertices, but interpolating schemes sacrifice the fairness for their interpolation.

Nonetheless, I feel that the fairness issues present less of a challenge to intuition than an approximating surface does. For example, in many cases, existing artwork can be used with interpolating schemes with some minor adjustments to smooth out rippling, whereas adapting existing polygonal art to be a control net for an approximating scheme is a much more difficult task.

Among interpolating schemes, the butterfly scheme has a number of things going for it. It's one of the better-researched schemes. It's also computationally fairly inexpensive. Finally, the results of subdivision tend to look good and conform fairly well to what intuition would expect. Therefore, it's my model of choice.

Butterfly in Review

If you haven't already, you probably should read my article from last month's issue for the deeper explanation of the modified butterfly scheme. But in case you haven't, I'll summarize it here. Given a triangular mesh, the control net, we want to subdivide it one step. We first add a vertex along each edge according to specific rules. If the endpoints of the edge are both of valence 6, then we use the stencil in Figure 1, with the weights:

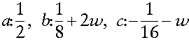
If one endpoint is of valence 6 and the other is extraordinary (not of valence 6) then we use a special stencil that takes into account just the extraordinary vertex, shown in Figure 2. The weights are computed as follows:

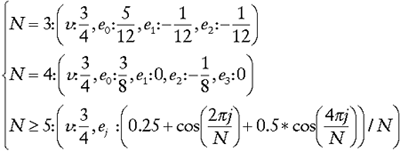
If both endpoints are extraordinary, we average the results of using the above extraordinary stencil on each of them. Again, if this seems a bit too terse, refer to last month's article where I discuss the scheme in substantially more detail.

As far as the butterfly scheme's characteristics, it's interpolating because points in a control net also lie on the limit surface - the subdivision process doesn't move existing vertices. It's also triangular as it operates on triangular control nets. It's stationary as it uses the same set of rules every time it subdivides the net, and uniform because every section of the net is subdivided with the same set of rules.

One aspect of the scheme that I mentioned last month but didn't define was the tangent mask of the butterfly scheme. This is the mask used to compute the tangent vectors explicitly at a vertex, which we use to find the vertex normals. The mask is large and therefore may look intimidating, but it's just a bunch of numbers, and a few multiplications and additions later, we've got the answer.

For regular vertices, the process involves the 1- and 2-neighborhood of the vertex (so it uses vertices that are one and two steps away.) Between both neighborhoods, there are 18 vertices, and so the scalars, corresponding to the indexing shown in Figure 3, are:

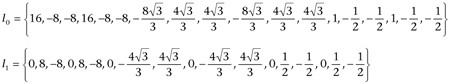
Multiplying the vertices by l0 and l1 gives us two different tangent vectors, the normalized cross product of which is our normal. For extraordinary vertices the normal is actually easier to find, as it depends only on the 1-neighborhood of the vertex. The two tangent vectors in this case can be found as:

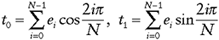
Here, t0 and t1 are the tangents, N is the vertex valence, and ei is the ith neighbor point of the vertex in question, where e0 can be any of the points (it doesn't matter where you start) and the points wind counterclockwise. Crossing the two resulting vectors and normalizing the result produces the vertex normal.

Implementation: The Big Idea

The idea behind our implementation is, at a high level, very straightforward. Given one control net, we want some piece of functionality that can take that net and output a more complex net, a net that has been advanced by a single subdivision step.

That sounds easy enough, right? Unfortunately, that description doesn't translate very directly to C++ code. So we need to define some of our terms and be more specific. First of all, what's a control net? We know what it is conceptually, but what kind of data structure is it and how is it manipulated? After that, of course, we need to define that "black box" bit of functionality that subdivides the net, and quantify how it works.

To establish our control net data structure, we start with nothing and build our way up as needed. So, the first thing we need is the base representation that will eventually pass into OpenGL. That's just a few arrays. We need an array for our vertices, our texture coordinates, and our colors. Furthermore, we'll need an array of indices into those arrays to define our faces; every three indices defines a triangle.

If we can do our tessellating with no more than that, then that's great. But chances are we're going to need to keep around more information than just that. The important thing is that whatever information is added to the data structure needs to be renewable. That is, since the process is iterative, the information we have in the simpler net coming in must also exist in the more complex net coming out, so that we can feed the complex net back in to produce an even more complex net.

It's worth asking why we'd need more information than just the vertices and faces. After all, if we need to determine whether one vertex is connected to another by an edge, we can determine that by looking through the faces. Or if we need to find all the edges, we could just do that by running through the face list, too. The problem here is in the running time of the lookups. When we're subdividing an edge, we need to find out a lot of information about nearby vertices and faces, and we'd like it to be as fast as possible. Regardless of the processor speed, looking through all the faces to find a vertex's neighbors will be slower than if we have that information available explicitly. This is because looking through the list of faces takes O(F) time, where F is the number of faces. On the other hand, if we have the information stored explicitly, it only takes O(1) time - constant time. That means that as we add more faces to the model, the former solution takes longer, whereas the latter remains the same speed.

We don't have the information we need to decide what else to add to the control net data structure, so we'll work on the procedure for subdividing a net and add data to the control net as necessary.

The Subdivision Step

Our task, then, is this: given a net, we need to subdivide it into a more complex net. Working from the modified butterfly rules, this is fairly straightforward. We need to add a vertex along each edge of the net. Then we need to split each face into four faces using the new vertices.

The first step, adding new vertices along each edge, tells us quite a bit about some more information we'll need in the control net data structure. There's no fast and simple way to find all the edges unless we store them explicitly. An edge needs to be able to tell us about its end points since we need to use those in the butterfly stencil for computing the new vertex. Furthermore, the stencil extends to the end points' neighbors, so the end point vertices need to know about the edges they're connected to.

The second step, breaking existing faces into new faces, requires that the faces know about their vertices, which they already do. The faces also need to know about their edges. While they could find this by asking their vertices for all their edges and fishing through them, that requires a fair amount more work for every lookup, and so we'll explicitly store with each face the information about its edges, too.

That increases the load a fair amount. Our data structure now has arrays of vertices, edges, and faces. Vertices know about their edges, edges know about their vertices, and faces know about their vertices and edges.

Graphs and Subdivision

It's worth noting that the data structure we're working with is nothing new and unusual. It's a specific example of a general data structure known simply as a graph. A graph is anything composed of vertices connected by edges. For instance, a linked list and a binary tree are both special kinds of graphs.

What makes our problem a little tougher than, say, writing a singly-linked list class is that the graph of vertices in a model is considerably more complex than the graph of nodes in a linked list. First, the nodes in a linked list have a single edge coming out of them (pointing to the next node) and one coming in (from the previous node.) Our graph has six edges coming into each regular vertex and potentially many more than that for extraordinary vertices.

Furthermore, in the case of a singly-linked list or a binary tree, the edges have direction. That is, you don't generally walk backward through the list or up the tree. Furthermore, these structures are acyclic - there are no "loops" in them - so from a given vertex, there's no path that leads back to the same vertex. In our case, the edges are undirected. You need to be able to traverse every edge in both directions.

Discussing graphs in this context is really just "interesting facts" rather than being a crucial contribution to our implementation, but it confirms what we already know: our data structure is complicated. The one saving grace is that our algorithm is based on locality, so we don't need to worry about traversing huge distances across the graph to find information we need to subdivide. This is one benefit of using a scheme with minimal support. A scheme with much broader support would be computationally much harder to evaluate, and hence be much slower and far more difficult to implement.

It also confirms the direction we're taking to implement the data structure - it's based wholly on locality so that the time it takes to find one vertex given another is proportional to the number of edges between them. There are other ways of representing graphs for the myriad applications that have different requirements. Cormen and his co-authors (see For Further Info at the end of this article) provide an excellent introduction to graph theory.

Control Net Details

So we know the data we need in our control net data structure and we know the steps the tessellation needs to execute. We're ready to dig into the lower-level implementation details. First, we'll go back to the information in the control net structure and look at how it should be laid out.

Listing 1 shows the layout of the data.

Listing 1. The Data Used to Represent the Control Net.

class ButterflySurface
{

public:
&nbsp...

protected:
&nbsp...

// Information about the vertices
&nbspint numVerts;
&nbspint vertCapacity;
&nbspfloat* verts;
&nbspfloat* vertNorms;
&nbspVertexEdges* vertEdges;
&nbspfloat* texCoords;
&nbspfloat* colors;

// Information about the faces;
// all faces are triangles.
&nbspint numFaces;
&nbspint faceCapacity;
&nbspint* faces;
&nbspint* faceEdges;

// Connectivity information,
// needed for tessellating.
&nbspint numEdges;
&nbspint edgeCapacity;
&nbspButterflyEdge* edges;
};

// Classes used in control net storage.
class VertexEdges
{
public:
&nbspVertexEdges();
&nbspVertexEdges(const VertexEdges& source);
&nbspVertexEdges& operator=(const VertexEdges& source);
&nbspint numEdges;
&nbspint edges[MAX_VERTEX_VALENCE];
};

class ButterflyEdge
{
public:
&nbspbool operator==(const ButterflyEdge& cmp) const;
&nbspbool operator<(const ButterflyEdge& cmp) const;
&nbspint v[2];
};

There tend to be two schools of thought on data layout. One method is dubbed the "structure of arrays" (SOA) and the other is the "array of structures" (AOS). The idea is that the SOA method stores multiple parallel arrays whereas the AOS method stores all the data interleaved in the same array. I've personally never run into a situation where the two approaches differed greatly in speed, and so when I lay out data I generally try to blend the two approaches for clarity's sake. That's why some of the data in the listing is shown as separate arrays of base types and some are stored as arrays of small objects.

The vertices are stored in OpenGL-friendly arrays. While OpenGL allows for interleaved arrays, many applications tend to store their data in parallel arrays, and that's why I choose to do so as well. The vertices, texture coordinates, normals, and colors each have their own arrays. These arrays are dynamically grown; when I need to add another vertex and there isn't sufficient room, I allocate new arrays that are twice the size of the current ones and move the data into the new arrays. This strategy amortizes the cost of memory allocation and is one I use for most of my memory management.

Each vertex also has a VertexEdges associated with it. VertexEdges keeps track of the edges that the vertex is a part of. Following the theme of making lookups as fast as possible, the edges are stored sorted by winding order, so each successive edge in the array is the next edge in counterclockwise winding order from the previous edge.

The edges themselves prefer the AOS format. Each edge is stored as nothing more than two indices into the vertex arrays. Adding another nitpicking detail, I sort the indices by value. It comes in handy as there are many cases where I can skip a conditional by knowing that they're in sorted order.

The faces are stored simply as an array of indices into the vertex arrays, where every three indices defines a triangle. Since the control net is totally triangular, I don't need any complicated support for variable-sized faces.

That's it for the storage of the control net. Now we need to understand the details of the tessellation process.

Subdivision Step Details

As mentioned earlier, the subdivision step consists of subdividing edges and then building new faces from them. The top-level function that does this is shown in Listing 2.

Listing 2. The Top-level Function Used to Tessellate a Control Net.

// This tessellates the surface.
void ButterflySurface::tessellate()
{
// Loop controls.
&nbspint x;

&nbspfor (int level=0; level
{
// This is how we later find the new
// vertices created along edges.
&nbspint* edgeVertMap = new int[numEdges];
&nbspfor (x=0; x
{
&nbspedgeVertMap[x] = -1;
}

// This is how we find the new other
// half-edge made when the edge is
// split.
&nbspint* edgeEdgeMap = new int[numEdges];
&nbspfor (x=0; x
{
&nbspedgeEdgeMap[x] = -1;
}

&nbsptessellateEdges(edgeVertMap, edgeEdgeMap);
&nbspbuildNewFaces(edgeVertMap, edgeEdgeMap);

&nbspdelete[] edgeVertMap;
&nbspdelete[] edgeEdgeMap;
}

// Only at the end here do we generate
// our normals.
&nbspgenerateVertexNormals();
}

For the edge subdividing, I iterate over the edges. At each edge, I check the valences of the end point vertices to determine which subdivision rules to use. Upon deciding that, I apply the rules and produce the new vertex. It's then added to the end of the vertices array.

Furthermore, the edge is split into two edges. One of them uses the slot of the old edge, and one of them is added to the back of the edge array. For use in building the faces, I keep two lookup tables. One maps from the old edge index to the index of the new vertex I just created. The other maps from the old edge index to the index of the new edge that I just added.

Building the faces is somewhat more involved, as it requires a fair amount of bookkeeping when creating the four new faces to be sure that they're all wound correctly and have their correct edges. For each face, I have the corner vertices and the edges. From the two lookup tables I created while subdividing edges, I also know the new vertices and new edges.

I shuffle all that data around to get it in a known order so that I can then build faces out of it. I also end up adding three more edges connecting the new vertices inside the triangle. Those new edges need to be added to the new vertices' edge lists, and they need to be added in the correct winding order. This isn't much code, but it's tricky and bug-prone.

Using this function, I can iterate over that as many times as I like. Each iteration increases the polygon count by a factor of four. When I decide to stop, only then do I need to worry about calculating vertex normals. Iterating over the vertices with the modified butterfly tangent mask finds those handily.

Colors and Texture Coordinates

The previously described procedure finds the vertices and normals, but not the colors or texture coordinates. These deserve their own discussion. Colors are nice because they can be interpolated using the same scheme as the vertices. If the butterfly scheme produces smooth surfaces in XYZ space, it will also produce smoothness in RGBA space. It's certainly possible to linearly interpolate the colors. That will result in colors that don't change abruptly, but whose first derivative changes abruptly, resulting in odd bands of color across the model, similar to Gouraud interpolation artifacts.

Texture coordinates are a somewhat more difficult problem. Current consumer hardware interpolates color and texture over polygons in a linear fashion. For colors, this isn't what we generally want: Gouraud interpolation of color exhibits significant artifacts. But for texturing, it is what we want. The texture coordinates should be linearly interpolated, stretching the texture uniformly across a face.

Therefore, when I interpolate texture coordinates during subdivision, I just linearly interpolate them. Furthermore, higher-order interpolation doesn't necessarily make sense at all, as different faces of the control net might have totally different sections of the texture, or even have totally different textures mapped onto them. While the data structure doesn't currently support this (vertices would need to be capable of having multiple sets of texture coordinates), it could certainly be desirable. In this case, neighboring vertices' texture coordinates are in totally different spaces, so interpolating between them doesn't make sense.

So, I'll stay with linear interpolation for texture coordinates. In terms of elegance, this method is a little disappointing. If we interpolated everything using the modified butterfly scheme, we could treat vertices not as separate vertex, color, and texture-coordinate data, but as one nine-dimensional vector, (x,y,z,r,g,b,a,u,v), and just perform all the interpolation at once. Alas, in this case, elegance needs to take a back seat to pragmatism.

Now we know how to start with a control net and step forward, producing increasingly detailed control nets, all the while keeping our data structures intact and keeping our vertices, colors, and texture coordinates intact, and generating normals for the finished model. What else is there left to cover?

Animation

While it's beyond the scope of this article to describe how you might implement a full animation system that uses subdivision surfaces, it's worth describing how subdivision surfaces and animation can coexist. If your game is one that stores the animated model as a series of full models, clearly you don't even have to think about it - subdividing those individual meshes will just work.

Skeletal animation is a somewhat more interesting problem. One of the nice things about subdivision surfaces is that a skeletal animation system should be able to transform the control net before subdivision, saving you the cost of multiple-matrix skinning on the high-polygon final model. This does have some downsides, though. Depending on the model and a host of other factors, the skeletal animation might cause the model to flex in strange ways or to exhibit increased rippling or unfairness.

The other downside is that it doesn't allow your application to take advantage of forthcoming hardware that supports skinning on the card. Depending on the speed of that skinning, though, and on how many times you subdivide the model, the savings of you doing a reduced number of transforms may or may not be worth the loss of offloading.

Adaptivity

Since this is a scalable geometry solution, it's worth asking if we can adaptively subdivide based on curvature or distance to the camera. In my previous Game Developer articles on tessellating Bézier patches ("Implementing Curved Surface Geometry," June 1999, and "Optimizing Curved Surface Geometry," July 1999) such adaptivity was a major focus.

The problem with adaptive solutions for subdivision surfaces is that, unlike patches, subdivision surfaces don't easily expose a closed-form parameterization. The only easy way to tessellate them is through recursion. So we rely on the fact that as we recurse, we're converging on a limit surface. And no matter how we tessellate, we should be converging on the same limit surface.

If we tessellate adaptively, we've changed the control net. Some of the net might be at a higher level of tessellation than the rest. And so we've broken the rules, and our net is no longer converging on the same surface. This is a worst case scenario for scalable geometry - it produces a "popping" that you simply can't avoid, since the underlying surface is now fundamentally different.

Furthermore, although this could probably be dealt with somehow, would it be worth it? Consider that a game probably won't be subdividing the control net more than four times. If your original net is, say, 1,000 polygons, four subdivision steps bring it to 256,000 polygons. The span of low-end to high-end machines isn't yet quite that large. So the end result of an elaborate adaptivity scheme would just be a model that was subdivided three times in some areas, maybe four in others: a whole lot of work for negligible benefits.

If you're using subdivision schemes for characters, then unless your characters are gigantic, adaptivity based on distance from the camera won't be worth much, either. Plus, characters tend to be fairly uniformly curved; most of them don't have large flat sections and jagged spikes in other areas. Therefore, in the end, you might be able to squeeze some benefits out of an adaptivity scheme, but the amount of work necessary to do so is fairly daunting. It's probably sufficient to pick a subdivision level based on distance to the camera and field-of-view angle and tessellate to it.

The Demo and Further Work

As promised, this article is accompanied by a demo built off the sample implementation provided above. A few screenshots are shown in Figures 4 and 5. The demo is available at my web site (see For Further Info at the end of this article) and comes with source code and a couple of sample models.

I'll freely admit that the demo is not at the point where you coulddrop it straight into your game and witness a stunning transformation (unless shiny salamanders are exactly what your game needs). There's a good deal more to be done with the demo. For starters, it's worth asking what to do when even the base control net is too dense. If a character is far away from the camera, maybe you'd only like to draw a 200-polygon version? In that case, integrating a separate mesh-reduction algorithm that you apply to the simplest net when needed could solve the problem nicely.

Another issue that the demo doesn't address is the question of caching. I currently regenerate the subdivision from the base net every frame. Is it worth caching subdivisions? On one hand, it could make things faster, but if the models being subdivided are characters, then the animation probably makes caching less useful, since the model you created in one frame isn't in the right position by the next frame.

Whether or not the modified butterfly scheme is the right one for you, this demo should provide a decent starting point for experimentation. Hopefully, between these two articles, I've given a solid overview of subdivision surfaces, and maybe even gotten somebody interested in using them in a game or two. Questions and comments are heartily encouraged, and in the meantime, I hope to find myself amazed by the next generation of fully scalable, beautiful games.

For Further Info:

The demo and other resources are available at my web site:
http://www.cs.dartmouth.edu/~bsharp/gdmag

Additional Resources

Cormen, T., C. Leiserson, and R. Rivest, Introduction to Algorithms. Cambridge, Mass.: M.I.T. Press, 1998.

Zorin, D. "Stationary Subdivision and Multiresolution Surface Representations." Ph.D. diss., California Institute of Technology, 1997. (Available at ftp://ftp.cs.caltech.edu/tr/cs-tr-97-32.ps.Z)

Zorin, D., P. Schröder, and W. Sweldens. "Interpolating Subdivision for Meshes with Arbitrary Topology." Siggraph '96. pp. 189-192. (Available from ACM Digital Library.)

When he's not sleeping through meetings or plotting to take over the world, Brian's busy furtively subdividing, hoping one day to develop his own well-defined tangent plane. Critique his continuity at [email protected].