Implementing Curved Surface Geometry

Remember Quake? Back when it was first released, consumer-level 3D acceleration was nearly unheard of, and id's software renderer scaled in speed with the clock speed of your Pentium processor.

During the few years since then, though, our market has reached a point of stratification with non-accelerated Pentium "Classic" machines on the low end and the latest and greatest pixel crunchers on the high end. The range is enormous. As game developers, it's important to support high-end consumers, and yet we'd prefer not to abandon the low-end players. From this desire was a new industry trend born: scalable geometry.

Scalable Geometry

Scalable geometry is any kind of geometry that can be adapted to run either faster with decreased visual quality or slower with increased visual quality. There are a number of ways of doing this, so we'll briefly cover the more popular methods.

One of the earliest methods used in games to scale geometry involved hand-generated level-of-detail models. You can see this principle at work in games like Battlezone and Grand Prix Legends. In the case of a race car, artists create a very high-detail model of the car, then a lower-detail model, and then continue down to a very low-detail model. Then, at run time, factors like the speed of the machine and the distance of the car to the viewer determine which model you use each frame. One of the benefits that hand-tuned LOD models have over other approaches is that the models can have more actual polygonal detail at the higher levels, since they're created by hand. There are many drawbacks, though. For instance, the switch from one model to another can manifest itself as an abrupt visual "popping", and can therefore be distracting to the viewer. A solution to this is to increase the number of LOD models, but this exposes another drawback: it takes a lot of an artist's time to make several versions of every object.

Another method of implementing scalable geometry is in using dynamic mesh reduction techniques. Shiny's, Messiah, uses a technique like this for their character animation system. The idea here is that you store one high-detail version of a model. Then, based on the distance of the model from the viewer and the desired framerate, you use some kind of detail reduction algorithm to generate an appropriate mesh. There are a number of ways to perform the detail reduction; if the high-detail model is stored as a polygon mesh, algorithms like the quadric error metrics described by Garland and Heckbert are perfect for the task. The advantages to dynamic mesh reduction are that many of the techniques can be very fast with some precalculation, and it can produce very good-looking results. There are, again, a number of drawbacks. It can be tricky to get texture coordinates to reduce with the mesh without making the texture slide around on the model. Also, algorithmically reducing a model from 10,000 polygons to 50 polygons still generally won't look as good as a 50-polygon model hand-crafted by an artist.

Curved Surfaces

The final method we'll mention, then, is the topic of this article. Curved surfaces are one of the most popular ways of implementing scalable geometry. There is a good reason for that, too; in games we've seen them in, they look fantastic. Unreal's characters looked smooth whether they were a hundred yards away, or coming down on top of you. Quake 3: Arena screenshots show organic levels with stunning smooth, curved walls and tubes. There are a number of benefits to using curved surfaces. Implementations can be very fast, and the space required to store the curved surfaces is generally much smaller than the space required to store either a number of LOD models or a very high-detail model.

The downside of curves and curved surfaces is that they are perhaps the most difficult of the three methods to learn and understand. There's a lot of reference material out there, but a lot of it is not easy reading, even if you know the material and are just using the books for reference. Therefore, in this article, we'll look at the basics of curves and curved surfaces. We'll cover the concept of the basic polynomial curve, and then onto two example curve representations: Hermite curves and Bézier curves. From there, we'll move onto surfaces, covering the Bézier patch. In this article, we'll take the most straightforward approach possible to rendering the curves and patches. While this does mean that our implementations will be very slow, they will hopefully be more legible for it. Next month, we'll continue our examination of patches by delving into optimization techniques to make them truly useful.

Remedial Curve Concepts

Just to be absolutely sure we all start off on the same wavelength, we'll start by reviewing some of the basic math principles that we need as a foundation for working with curves and curved surfaces. Feel free to skip this section if this is remedial.

At its core, any of the curves we'll discuss can be represented as a parametric polynomial function. Following convention, we'll use the parameter u. Our curves will look something like this:

Generally, we'll refer to f(u), which is the 3D point on the curve at u. Now, as long as at least one of c0, c4, and c8 are non-zero, the curve will be a cubic curve, and cubic curves are the ones we're most interested in. After all, since we'd like to keep computation to a minimum, we'd like to use the lowest-degree curve possible (since a higher degree requires more multiplication every time it's evaluated). So, we might try using a zero-degree curve (which would be fast to compute). But a zero-degree curve is simply a point, which doesn't do us too much good.

Moving on, a one-dimensional curve is simply a line. It's pretty clear that lines are insufficient for our purposes. So, we move on to quadratic curves. These are parabolas, which might seem sufficient for representing curves and curved surfaces. Unfortunately, second-degree curves will always lie in a plane, and we're working in three dimensions, so it would be better to have a space curve, a curve that isn't confined to two dimensions or less. Therefore, our cubic curve is the curve of choice.

Representations

So all a programmer needs to do is code up a quick tool for the artists consisting of a view window and four text entry boxes for them to type in the coefficients of curves, right? Of course not - artists demand flexibile, intuitive tools, and it's clear that creating curves by typing in coefficients lacks that certain ease-of-use factor for most of us. Therefore, we need another representation for the curve that makes creation and manipulation more intuitive. We'll touch on two such representations, the Hermite curve and Bézier curve.

The Hermite curve we cover both because it's fairly common, but also because it doesn't require any specialized formulae to understand it. Then, as Bézier curves are somewhat more versatile, we'll move on to them. While we won't discuss it here, converting from Bézier curves to Hermite curves and vice versa is very straightforward and is explained in the references at the end of the article.

There are plenty of other curve representations that we aren't going to touch upon. Notably, we are not going to cover B-Splines or that family (including the pervasive NURBS), of which Bézier curves are simply a special case. I chose the Hermite and Bézier curve models as a good starting point, because they can be represented and understood with a fair degree of ease. Once you have a firm grasp on Bézier curves, picking up one of the references at the end of this article and learning more about other curve models is much easier.

Hermite Curves

A Hermite curve is a cubic curve described by its endpoints p0 and p1 and the tangent vectors at the endpoints, v0 and v1. You can see in Figure 1 what an example curve looks like.

The question, then, is how we get the cubic equation from the points and vectors. Hermite curves are nice this way, as the derivation of the cubic is possible with just a little calculus. Let's say our cubic equation is

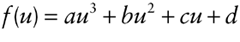
Note that f(u), a, b, c, and d are vectors. Then, we have that:

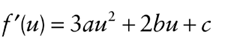
Then, we can express the endpoints as f(0) and f(1), and the tangents as f'(0) and f'(1).

Solving now for a, b, c, and d, we get:

Eq. 1

Then we'll solve for what are called the "basis functions." The basis functions are simply functions of u that determine the contribution of the endpoints and tangents along the curve. So, for instance, the basis function that corresponds to p0 determines how much p0 contributes to points along the curve. Just by rearranging terms once again, we have the basis functions.

Then, we can express the curve as the sum of the basis functions times the components:

This provides us a handy way of expressing the curve. Furthermore, basis functions become far more important when we discuss Bézier curves, and so the Hermite curve provides a good introduction to the idea of a basis function.

So, as we see here, a basis function is nothing more than a function associated with a component of the curve that determines the contribution of that component to points along the curve.

Implementing Hermite Curves

As handy as the basis functions are for expressing the curve, it's easier for our naïve implementation just to calculate the cubic equation of the curve by finding the coefficients using Equation 1. The code that does this is shown in Listing 1.

Listing 1. Code to generate a cubic parametric equation from a Hermite curve's endpoints and tangents.

void genCubicFunction()
{
// Do this so we can treat each endpoint and tangent //vector as a separate array.
float* p0 = points;
float* p1 = points + 3;
float* v0 = tangents;
float* v1 = tangents + 3;
// Do this so we can treat each vector coefficient //of the function as a separate array.
float* a = functionCoeffs;
float* b = functionCoeffs + 3;
float* c = functionCoeffs + 6;
float* d = functionCoeffs + 9;
// Now, generate each coefficient from the //endpoints, tangents, and the predefined basis //functions.
//Note that we loop once each for the x, y, and z //components of the vector function.
for (int lcv = 0; lcv < 3; lcv++)
{
// a = 2p0 - 2p1 + v0 + v1
a[ lcv ] = (p0[ lcv ] + p0[ lcv ]) - (p1[ lcv ] + p1[ lcv ]) + v0[ lcv ] + v1[ lcv ];
// b = -3p0 + 3p1 - 2v0 - v1
b[ lcv ] = - (p0[ lcv ] + p0[ lcv ] + p0[ lcv ]) + (p1[ lcv ] + p1[ lcv ] + p1[ lcv ]) - (v0[ lcv ] + v0[ lcv ]) - v1[ lcv ];
// c = v0
c[ lcv ] = v0[ lcv ];
// d = p0
d[ lcv ] = p0[ lcv ];
}
}

Then, we just run along the curve by starting u at 0 and incrementing it by some fixed amount until we reach 1. We evaluate the curve at each value of u, save each result as a point on the curve, and then render the curve as a line strip. The code to evaluate the curve at a given value of u is quite simple and is shown in Listing 2.

Listing 2. Code to evaluate a cubic parametric
equation at a given value of u.

// This function simply computes au^3 + bu^2 + cu + d //for a specific u and stores the vector result in out.
void evaluateAt(float u, float* out)
{
// Do this so we can treat each vector coefficient // of the function as a separate array.
float* a = functionCoeffs;
float* b = functionCoeffs + 3;
float* c = functionCoeffs + 6;
float* d = functionCoeffs + 9;

// Note that we use Horner's rule for computing // polynomials (which is the way we nest the
// multiplies and adds to minimize the computation // we need.)
out[ 0 ] = ( ( ( a[ 0 ] ) * u + b[ 0 ] ) * u + c[ 0 ] ) * u + d[ 0 ];
out[ 1 ] = ( ( ( a[ 1 ] ) * u + b[ 1 ] ) * u + c[ 1 ] ) * u + d[ 1 ];
out[ 2 ] = ( ( ( a[ 2 ] ) * u + b[ 2 ] ) * u + c[ 2 ] ) * u + d[ 2 ];
}

It's worth noting that even though the curve is recalculated fairly slowly every frame, the frame rate is still in the high hundreds (well, on my Voodoo2 graphics card, at least). Since we're doing nothing but calculating a hundred or so points along a curve every frame, the speed hit as a result of this inefficiency is not yet apparent.

Bézier Curves

Now that we understand the cubic Hermite curve and its implementation, we can move on to Bézier curves. Whereas a Hermite curve is defined by endpoints and tangents, a cubic Bézier curve is simply described by four ordered control points, p0, p1, p2, and p3. Figure 2 shows an example curve.

Our problem now is that it's not immediately clear how we define the curve based on these four points. With Hermite curves, we could use some basic calculus to get a cubic parametric equation. But even if we say that p0 and p3 are the endpoints, the points p1 and p2 seem to have little bearing, analytically, on the curve. It's easy enough to say that the curve should "bend towards" the points, but what does that give us in terms of our cubic equation? Here's where the importance of our basis functions comes in. We need to find a set of functions that blend the control points together in ways that give us the curve that we want.

To do that, of course, we need to define the properties we'd like the curve to have. We can summarize these with three qualities:

Luckily for us, there exists just such a set of functions. These functions are called the Bernstein basis functions, and are defined as follows:

The parenthesized block with the n and the i is the mathematical phrasing of the binomial coefficient normally phrased "n choose i" or "n nCr i". The formula for n choose i is:

If we were considering general Bézier curves, we'd have to calculate that. Since we're only considering cubic curves, though, n = 3, and i is in the range [0,3]. Then, we further note that n choose i is the ith element of the nth row of Pascal's triangle, and so we have our values, {1,3,3,1}. So we can just hard-code that, no computation necessary.

While the Bernstein basis functions are a little odd looking at first, they're not that bad. To show that they really do satisfy our three conditions, we refer to Figure 3. This is a graph of the cubic basis functions. The red curve corresponds to p0, the green to p1, the blue to p2, and the magenta to p3. They're pretty looking, but what do they mean? Recall that the basis functions determine the contribution of each point over the curve. Also, the horizontal axis on that graph is u. So, when u is zero, the value of the basis function for p0 is 1, and all the others are 0. Therefore, the starting point of the curve is:

Therefore, we have that the curve starts at p0. Looking at the basis functions, it's obvious that the curve ends on p3. Our first condition is satisfied.

As for the local control, we can convince ourselves that this holds by staring at the basis functions for long enough. It's obvious that p0 and p3 have local control, because as we move them, the curve moves, and they have very little influence over the rest of the curve. We can also see, then, that p1 and p2 have local control, since they have the most influence over the curve 1/3 of the way and 2/3 of the way along the curve, respectively. That means that if we moved p1, it would pull the section 1/3 of the way along the curve with it, and affect the rest of the curve much less.

Then, we have our final condition: the curve must remain within the convex hull of the control points. With the Bernstein basis functions, this is true. The proof, however, is fairly complicated, and ends up dragging a bevy of new concepts into the fray. For the interested, Farin does a reasonable job of explaining this. It has to do with the fact that the Bernstein basis functions are nonnegative for u in the range [0,1], and also that if you sum up the values of all the basis functions for any value of u, the result is always 1.

Then, the formula for calculating a point on our Bézier curve is:

Eq. 2

Implementing Bézier Curves

Our approach to rendering a Bézier curve is similar to that for rendering Hermite curves. We find a series of points along the curve, and render that series as a line strip. We'll do it, once again, by evaluating the curve at even intervals of u. Listing 3 shows this clearly: UniformCurveTessellator::tessellate takes a vector of four control points and a vector of four associated basis functions, and renders the curve in 100 steps.

Listing 3. Code that tessellates and renders a Bézier curve as an evenly-spaced series of line segments.

void UniformCurveTessellator::tessellate( const std::vector< CurvePoint >& controls,
const std::vector< BasisFunction >& bases ) const
{
// We break the curve into 100 even increments of u.
int numSteps = 100;

// We can multiply by this in our loop instead of // dividing by (numSteps-1) every time.
double invTotalSteps = 1.0f / (numSteps - 1);

// Start drawing our curve.
::glBegin( GL_LINE_STRIP );

for ( int step = 0; step < numSteps; step++ )
{
// Generate the parameter for this step of the // curve.
float u = step * invTotalSteps;

// This holds the point we're working on as we // add control points' contributions to it.
float curPt[ 3 ] = { 0, 0, 0 };

// Generate a point on the curve for this step.
for ( int pt = 0; pt <= 3 ; pt++ )
{
// Get the value of this basis function at // the current parameter value.
float basisVal = bases[ pt ]( u );

// Add this control point's contribution // onto the current point.
curPt[ 0 ] += controls[ pt ].getX() * basisVal;
curPt[ 1 ] += controls[ pt ].getY() * basisVal;
curPt[ 2 ] += controls[ pt ].getZ() * basisVal;
}

// Draw this point.
::glVertex3fv( curPt );
}

::glEnd();
}

To generate each point, it calculates Equation 2 for the input - it adds up the sum of each point times that point's basis function. For our cubic curve, this is certainly not the most optimized way to calculate the curve. However, because it's only 100 points, it's not noticeable and the demo still runs quite fast.

Surfaces: The Bézier Patch

It might seem more consistent to cover not only Bézier patches but also Hermite patches, as well. The reason we're skipping straight to Bézier patches is that we're trying to cover the curves and curved surfaces in the most intuitive order possible. Whereas it makes sense to cover Hermite curves and then Bézier curves, Hermite patches are somewhat more difficult to learn than Bézier patches.

Since a Bézier curve was a function of one variable, f(u), it's logical that a surface would be a function of two variables, f(u,v). Following that logic, since a Bézier curve had a one-dimensional array of control points, it makes sense that a patch would have a two-dimensional array of control points. We'll now discuss bicubic Bézier patches. The phrase "bicubic" simply means that the surface is a cubic function in two variables - it is cubic along u and also along v. Then, since our cubic Bézier curve had a 1¥4 array of control points, our bicubic Bézier patch has a 4¥4 array of control points. Figure 4 shows an example of a surface.

Now, with that, we need to take our equation for evaluating a Bézier curve at some u and extend it to allow us to evaluate our patch at some (u,v). The extension is fairly straightforward. We just evaluate the influence of each of the 16 control points, yielding:

Eq. 3

We can see by inspection that our properties from the Bézier curve extend to the patches. Why? For the following reasons.

Implementing Bézier Patches

Rendering a Bézier patch is more complicated than rendering a Bézier curve, even when doing it in the simplest possible way. With a Bézier curve, we could just evaluate a number of points and render a line strip. With a patch, we need to evaluate strips of points and render triangle strips. Also, with a patch we have to worry about lighting. After all, an unlit patch will just look like an oddly-shaped splotch of red on the screen. To see the contours, we need lighting. For our naïve implementation, that means we'll need to light each vertex. To light a vertex, we need its normal. So, for every (u,v) pair, we need to solve for the point on the surface, and then solve for its normal.

Equation 3 tells us how to find the point on the surface, but how do we find the normal? Well, we know we can take the derivative of the surface with respect to either u or v, which would yield the tangent vectors to the surface in the direction of either u or v, respectively. If we find both of those tangents, we know that they both lie in the plane tangent to the surface. Then, taking their cross product will yield a mutually perpendicular vector, the surface normal. Finally, we'll have to normalize it since it most likely won't be unit length.

So, how do we find df(u,v)/du and df(u,v)/dv? As it turns out, we can just take the derivatives of the basis functions. That is,

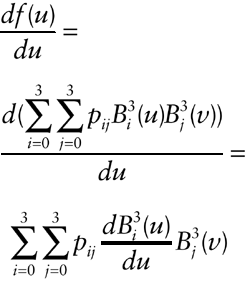
Eq. 4

The same holds for the derivative with respect to v. Therefore, before rendering, we calculate the derivatives of the basis functions and store them. We use Equation 4 and its v analogue to find the tangents, and then proceed to find the surface normal. The code for the loop is shown in Listing 4.

Listing 4. Code that tessellates and renders a Bézier patch as an evenly-spaced grid of triangles.

void UniformPatchTessellator::tessellate( const std::vector< std::vector< CurvePoint > >& controls, const std::vector< BasisFunction >& bases ) const
{
// We break the patch into a numSteps x numSteps // array of points.
int numSteps = 10;
// First, we need to make the basis functions for // our normals, which just involves taking the // derivative of each basis function.
std::vector< BasisFunction > bases_deriv( bases );
for ( int i = 0; i <= 3; i++ )
{
bases_deriv[ i ].differentiate();
}
// Now we generate the points and normals.
float* verts = new float[ 3 * numSteps * numSteps ];
float* norms = new float[ 3 * numSteps * numSteps ];
double invTotalSteps = 1.0f / (numSteps - 1);
for ( int stepU = 0; stepU < numSteps; stepU++ )
{
// Generate the parameter for this step of the // curve.
float u = stepU * invTotalSteps;
for ( int stepV = 0; stepV < numSteps; stepV++ )
{
// Generate the parameter for this step of // the curve.
float v = stepV * invTotalSteps;
// This holds the point we're working on as // we add control points' contributions to
//it.
float curPt[ 3 ] = { 0, 0, 0 };
float curNorm[ 3 ] = { 0, 0, 0 };
float curUTan[ 3 ] = { 0, 0, 0 };
float curVTan[ 3 ] = { 0, 0, 0 };
// Generate a point on the curve for this // step.
for ( i = 0; i <= 3; i++ )
{
for ( j = 0; j <= 3; j++ )
{
// Get a few basis function values // and products thereof that we'll // need.
float bu = bases[ i ]( u );
float bv = bases[ j ]( v );
float dbu = bases_deriv[ i ]( u );
float dbv = bases_deriv[ j ]( v );
float bu_bv = bu * bv;
float bu_dbv = bu * dbv;
float dbu_bv = dbu * bv;
// Add this control point's // contribution onto the current // point.
curPt[ 0 ] += controls[ i ][ j ].getX() * bu_bv;
curPt[ 1 ] += controls[ i ][ j ].getY() * bu_bv;
curPt[ 2 ] += controls[ i ][ j ].getZ() * bu_bv;
// Add this point's contribution to // our u-tangent.
curUTan[ 0 ] += controls[ i ][ j ].getX() * dbu_bv;
curUTan[ 1 ] += controls[ i ][ j ].getY() * dbu_bv;
curUTan[ 2 ] += controls[ i ][ j ].getZ() * dbu_bv;
// Add this point's contribution to // our v-tangent.
curVTan[ 0 ] += controls[ i ][ j ].getX() * bu_dbv;
curVTan[ 1 ] += controls[ i ][ j ].getY() * bu_dbv;
curVTan[ 2 ] += controls[ i ][ j ].getZ() * bu_dbv;
}
}
// Now get our normal as the cross-product // of the u and v tangents.
curNorm[ 0 ] = curUTan[ 1 ] * curVTan[ 2 ] - curUTan[ 2 ] * curVTan[ 1 ];
curNorm[ 1 ] = curUTan[ 2 ] * curVTan[ 0 ] - curUTan[ 0 ] * curVTan[ 2 ];
curNorm[ 2 ] = curUTan[ 0 ] * curVTan[ 1 ] - curUTan[ 1 ] * curVTan[ 0 ];
// Normalize our normal (ouch!)
float rInv = 1.0f / sqrt( curNorm[ 0 ] * curNorm[ 0 ] + curNorm[ 1 ] * curNorm[ 1 ] +
curNorm[ 2 ] * curNorm[ 2 ] );
curNorm[ 0 ] *= rInv;
curNorm[ 1 ] *= rInv;
curNorm[ 2 ] *= rInv;
// Store these.
memcpy( verts + ( stepU + ( stepV * numSteps ) ) * 3, curPt, 3 * sizeof(float) );
memcpy( norms + ( stepU + ( stepV * numSteps ) ) * 3, curNorm, 3 * sizeof(float) );
}
}
// We render each strip of the surface out as a // triangle strip.
for ( int stepV = 0; stepV < numSteps - 1; stepV++ )
{
int y0 = stepV;
int y1 = stepV + 1;
::glBegin( GL_TRIANGLE_STRIP );
for ( int stepU = 0; stepU < numSteps; stepU++ )
{
int x0 = stepU;
glNormal3fv( norms + ( x0 + ( y0 * numSteps ) ) * 3 );
glVertex3fv( verts + ( x0 + ( y0 * numSteps ) ) * 3 );
glNormal3fv( norms + ( x0 + ( y1 * numSteps ) ) * 3 );
glVertex3fv( verts + ( x0 + ( y1 * numSteps ) ) * 3 );
}
::glEnd();
}
// Clean up after ourselves.
delete[] verts;
delete[] norms;
}

Now, while the curves didn't slow down from our naive implementations, this patch demo shows quite painfully why optimization is very necessary. It runs at a steady 30 or so frames per second (again, on my Voodoo2), but that's just one patch. If you tried to base a terrain system on this implementation, it would be painfully slow. After all, consider the work we're doing. By default, the tessellator breaks the surface into 100 points. At each point, we're evaluating 32 cubic functions and 32 quadratic functions, then doing a vector cross-product and a vector normalization (ouch!). Then, for each point, we're asking OpenGL to light it, which is not cheap either. Plus, we're not caching any of this between frames, and we're actually allocating and then deallocating the space every frame. So we're doing a lot of work, much of it entirely unnecessary.

Nonetheless, it works. We're rendering a lit Bézier patch, and even if it is a bit sluggish, it looks pretty good. Now, if only we could do something with it...

Moving from Theory to Application

There are certainly a number of loose ends. We've covered Bézier and Hermite curves and Bézier patches, but the implementations so far are entirely unoptimized and the patch demo is rather sluggish even for what little it is supposed to do.

Furthermore, we haven't seen an example of using these things in a real application. The demo code is just that - a demo of a curve or surface floating in black space. There is still a fair amount of material to cover before we can turn these into something real.

Next month, I'll cover some optimization techniques for Bézier curves and surfaces. We'll also see how to form other surfaces and objects by joining Bézier patches together, and look at some of the properties of such objects, as well as some of the problems that can arise from the new techniques. Finally, having covered all of this, I'll finish off the article with a far more interesting demo.

References

When he's not sitting around radiating potential, Brian's probably busy furthering the secret OpenGL agenda. Either that, or he's likely doing the same thing he does every night, Pinky - trying to take over the world. Send preemptive bribes and/or tribute to [email protected].