Dependency Graphs In Games

Everyone who has ever worked with a game engine has, at some point, stumbled across data dependency problems. Relationships between objects and data are everywhere. When rendering a frame of the game, data from that frame needs to be processed in the correct order to get the proper view of your data. If the order is incorrect, the renderer can display data that's a frame behind where it should be.

For instance, imagine a car driving in your game, while a camera observes it. You want the camera to look precisely at the car as it is rendered. Assuming the car is moving, it will be updated each frame. But if the camera orientation is updated before the car's transform is updated, the camera will be looking at the old position of the car - it's location in the previous frame. If the frame rate is high enough and if the objects aren't moving too fast, this error may be very small. But in more extreme cases, it can be a big problem. For example, in our upcoming game, Xyanide for the Xbox, we have a spaceship flying at two kilometers per second. If our camera tracks our spaceship's position before it updates, it is looking about 30 meters behind the spaceship (at 60 frames per second). In this case, that's significant.

If you're not yet convinced of the benefit of updating your data in the correct order, this might convince you: when using a scene graph, calculating the world transformation matrix in the scene graph tree can be a very costly operation. The calculation is usually optimized by setting dirty flags in the scene graph. The goal of these dirty flags is to update the world transform of the objects as little as possible, preferably just once before rendering. Now imagine what happens if we have two objects, A and B. B is part of a scene graph, and has a parent. Object B moves each frame. If A uses B's world transformation matrix before B is updated, the calculation of B's world transformation matrix is performed twice: once when A uses it, and once before rendering, because B's update caused its world transform matrix to be marked dirty again. Naturally, this is a problem.

The goal of this article is to discuss object dependency problems like these in games, and offer some solutions. But frankly, the solutions provided aren't the primary focus for my writing this article. Above all, I would like to make game programmers aware of the relationship and dependency problems that exist in game programming. Since transformation matrices cause the most obvious dependency problems, I will focus on them. However, data dependency problems apply to any form of data.

The article is structured in three parts. The first part of this article discusses problems that arise in dependency graphs, the second section shows some solutions for a-cyclic dependency graphs, and the final section discusses cyclic dependencies and eventually expands a solution from part two into a solution for a cyclic dependency graph.

Breaking Down The Problem

Source and Target Nodes

Let's take a look at the main loop. Here are the update steps a single frame might require:

In game programming it's normal to update your events each frame. The game clock that's used for this purpose is usually maintained within the main loop. The polling of input devices is usually also hardcoded in the main loop. But why aren't the game clock and input devices treated like any other node?

The order in which these hardcoded operations are called is based upon the implicit dependencies between nodes. The collision code is dependent upon the nodes, and the nodes are dependent upon both the input devices and the gameclock. The renderer depends of all of them. So let's make all of them nodes, and create dependencies between them.

Let's examine the importance of a single timeframe. During a single timeframe the game updates data, which in turn is used to produce output on a physical device, like a monitor or the speakers. (The render operation is an example of how data can be turned into output on a physical device.) Apart from the nodes that produce output for physical devices, each node always has another node that depends on it. If this isn't the case, the node has no practical use.

A node is called a "root node" or "source node" if no other nodes depend on it. The gameclock and the node that polls for device input are good examples of source nodes. A node is called a "target" node if it produces output to physical devices. All other nodes ("common nodes") depend on other nodes and have nodes that depend on them.

Relationships

Let's take a look at some relationships between nodes.

Relationship 1: Traditional Hierarchical Dependency

If node C uses data from node B, this means that C depends upon B. Node B must therefore be updated before node C uses it. In the timeframe, we want to update node B before node C is updated.

Example: We have a camera (C) and a moving target (B). If we want the camera to look at the target, the position of the target must be updated before the camera orientation is calculated. But what if node B was part of a scene graph, and it had a parent? The camera would need node B's worldtransform. That implies that C depends on both node B and its parent, which we'll call node A. Figure 2 shows this relationship.

We can argue that node B shouldn't be dependent upon node A - rather, that C should just be dependent upon node B, as shown in figure 3. But node B doesn't necessarily depend on its parent node if it's not using its own world transform! If no other node uses node B's world transform, this relationship is obsolete. On the other hand, if we omit the dependency between node B and node A, the observer would need knowledge of the subject's scene graph parents to get the correct world transform, and that's not ideal either. The choice is yours.

Relationship 2: Dependencies Not Known

In this type of relationship, node A can write data in node B. Node B does not have to know about this relationship, and therefore does not know that it now depends on node A.

Example: An input node that reads controller input and sets the transform of the car node. If the car node wants to use the correct transform, the input node must be updated first.

Relationship 3: Traditional Circular Dependency

In this relationship, a data member of node A can depend on a data member of node B, and vice versa.

Consider three points in space that (naturally) form a triangle when lines are drawn between them. The constraint between these points is that the distance from a given point to its adjacent points must remain constant. Therefore, if I move one of the points, the other points must move along with the dragged point without deforming the shape.

Relationship 4: Solvable Circular Dependency

Here is another form of circular dependency between nodes. Node A contains data members X and Y, and node B contains data members V and W. X is depends upon V, and W depends upon Y (see figure 7). In this case, there is a circular dependency at the node level, while functionally there is no dependency at all.

Relationship 5: The Data Processor

In this situation, a node does not contain data -- it only processes it. It always depends on one or more other nodes for input, and it will always output data to other nodes, as it cannot store the calculated data itself.

Often, node B will process data from a series of nodes, and also write back into these nodes. For example, imagine a collision-detection-and-response node that takes all of the node's transforms, sizes, speeds and so on, and writes the new data back into the input nodes.

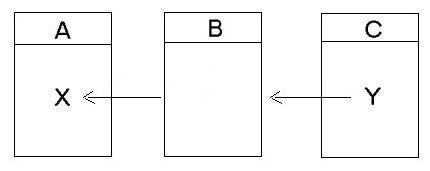
Figure 8: Node B contains no data. Note that the relationship between node B and C is the same as shown in relationship 2.

Relationship 6: Multiple Dependencies

A node can depend on another node multiple times. For instance, imagine an AI enemy that slowly steers towards a target, but at the same time it's shooting at the target. If the "shooting" dependency is dropped because the enemy stopped shooting, the "steering" dependency may still be relevant.

Scene Graph Versus Dependency Graph

At first look, it can be tempting to use the scene graph as your dependency graph. When retrieving an object's world transform, quite often it's obvious that you want its scene graph parents to be updated first. While this may hold for many cases, it fails for many others. For example, the observer relationship is quite hard to implement in a tree-like graph. An observer should be updated later in the timeframe then its subject. To do so, the observer must either be:

This just doesn't sound good to me, and I'm not even mentioning the fact that observers should be able to switch subjects, or the fact that this method excludes dependencies to any other form of data.

Define Your Atoms

Let's take a look at relationship 4 again, the solvable circular dependency (shown in figure 7). It's a circular dependency between nodes. In object-oriented languages we are prone to create dependencies between functionally grouped data members, like a C++ object having multiple data members. As soon as your objects contain multiple data members and other objects depend on one of these data members, the problem shown in relationship 4 is bound to arise. An example of such a situation is when object A uses object B's translation data, and object B in turn uses object A's rotation data. Making this problem even trickier is that the translation and rotation data likely must be included in a single 4x4 matrix!

In our game, we have a similar situation. We have a node that is similar to a viewport, through which we see our ship. The ship determines its own world transform, but its rotation depends on the viewport's rotation. In turn, the viewport's translation depends on the ship's translation, as the viewport can scroll left/right/up/down to keep the ship visible.

Splitting the objects into smaller objects, as shown in figure 11, can solve this dependency problem. The viewport didn't necessarily need to be split up, but it is displayed this way for clarity.

So you should consider what level you want to define your relationships. Are you content with relationships between objects that contain data sets, or would you prefer to depend on each single data member? And what if you have a 3D vector -- is it sufficient to be able to depend on the vector as a whole, or do you want tobe able to depend of each element in the vector? We could continue this down to the byte level. That sounds silly, but professional 3D animation packages cannot do without dependencies at, say, the vector level.

Dynamically Created Objects In The Dependency Graph

When nodes are created dynamically, it's possible that they will be created during the update sequence. When adding the node to the dependency graph, you don't know whether it will be updated during this update loop, prior to rendering it. You might wonder whether updating this node during the same loop is proper behavior at all.

Personally, I think it's best to create dynamic objects with proper initial values and ensure that the node isn't updated that frame. For instance, when shooting a bullet from a cannon on a spaceship, I set the bullet's initial transform to be the location of the cannon on the ship. When rendering its first frame, I want the bullet to be visible at the cannon's mouth. If that position were then updated right away, it would no longer appear at the mouth of the cannon. I raise this issue because I have never seen a case where it mattered whether a node was created in the beginning or at the end of the update timeframe -- most of the time your node will seem to run one frame ahead.

A-Cyclic Dependency Graphs

This section explores three simple solutions for a-cyclic dependency graphs.

Example 1: The Framecaller

At the former company I worked for, we used a system called the framecaller. It's not very fancy, and it's actually very easy to use. With this solution, each node has a framecaller (parent node). This parent node is responsible for updating its children. Just like a scene graph, each node has a single parent node and a list of child nodes. If node A is dependent upon node B, node B will set its framecaller to node A. When switching framecallers, as is needed when switching observers, the old framecaller needs to be notified so it can remove its child node from its list.

Please treat the example code in this article as pseudo code, as it is far from complete. It is just to give you an idea of how it could be implemented.

Note that this system has its drawbacks. As with the problems raised by scene graphs vs. dependency graphs, trees are not great for handling observer relationships. When constructing a simple observer relationship, the observer needs to set the framecaller for its subject to itself:

This is the only way for it to work, since most of the time the subject does not know it is being observed. But what if there were multiple observers -- say, 10 rockets homing in on a target? They would all try to set the framecaller to themselves, probably resulting in erroneous update orders for some fellow rockets. There is another disadvantage, too: it is not very easy to extend this method into one capable of handling cyclic dependencies. On the other hand, the advantage to this system is that the pointer overhead is minimal.

Example 2: Pulling

I call this solution "pulling" because the target nodes pull data out of the nodes they depend on. It's a system I implemented for the company I currently work for, and like the last method, it's easy to implement. Also, as before, the implementation shown below is not technically challenging; what's most important is recognizing the relationships and knowing how to deal with them.

In the pulling method, each node has a list of nodes upon which it depends. If a node is already updated, it won't be updated again. All nodes receive an update call, and each node will call the Update method of their dependant nodes first.

But where do you start updating in this scheme? We could solve this using brute force: make a list of all the nodes in the game loop and simply start updating them one by one. Unfortunately, this would result in a lot of unnecessary update calls, because often, the update will have already been performed. The better choice is to update just the target nodes. If your target node is the renderer, it will update the complete dependency graph until it is ready to render. This will result in far fewer unnecessary update calls.

The benefits of this method are that it can easily handle observer relationships and it can be extended to handle cyclic dependencies. Its disadvantage is its memory use, and the fact that there may be some extra update calls (the nodes that already have been updated). If the performance overhead gets out of hand, add an extra caching list to the game. This caching list should contain the correct update order for a frame, and each node should be in the list just once. It can be computed very easily, but the list must be marked dirty whenever nodes are deleted or constructed, or whenever relationships between nodes change.

Example 3: Pushing

This method is essentially the opposite of the previous example: it is an event-driven method. I call it the "pushing" method because the source nodes push their changes onto their dependees.

Pushing has one very nice property: if a node hasn't changed, you know that there is no need to update its dependees. Instead of using a "dependant of" list, we use a "dependee" list, which is a list of nodes which depend on it. This method does not need much explanation. A node should always perform its own update first, and then notify its dependees of the change. Instead of starting off with the target nodes, it starts off with the source nodes.

This method is much like the "pulling" method, but it has two drawbacks:

Cyclic Dependency Graphs

Cyclic dependencies are best avoided in games. Why? First, the solutions can be quite complex. But the biggest reason to avoid them is that they cause performance problems. Usually a maximum number of iterations is set to prevent a game from running into an infinite loop and keep control over the performance. So for the handful of cyclic dependencies developers are likely to encounter, they are dealt with case-by-case, not by writing a generic system to deal with them.

With current hardware, this is probably the best approach. Each case can be optimized since you usually have intimate knowledge about each case. We also tend to ignore small errors, because the deviation is barely noticeable. Consider collision response: typically you update your nodes, perform collision detection and response, and then render. What you should really do is: update the nodes, perform collision detection and response, and then update the nodes that have moved because of the collision response. Otherwise, to use the camera example again, the camera would look at the incorrect position of its target -- the position of the target before the collision response was calculated.

Although I think cyclic dependencies are better handled case by case, I will expand the functionality of the "pulling" example of the previous chapter so it is able to handle cyclic dependencies. When dealing with a cyclic dependency, you need to break the cycle some somehow. The most obvious way is to stop it when either one of the nodes stops changing value.

To protect system performance and prevent infinite loops, the solution below limits itself to a maximum number of iterations for each node. The example consists of three nodes: A, B and C. A is a dependent of B, and B is dependent of C. Node C, in turn, is a dependent of node A (figure 13).

The first question I would want answered about this problem is, "If A is a dependent of B and B is a dependent of C, is A then automatically a dependent of C?" That an uncertainty, especially if a node contains multiple data members. It could very well be possible that node A uses node C's data differently than does node B. We shall see why this is important in a moment. For now, however, we can conclude that we are better off setting our dependencies explicitly, as shown in figure 14.

If we used the "dependent of" list from example 2 in the previous section to create the relationship between node C and A, we would end up creating an infinite loop. Instead, let's mix this "dependent of" list with the "dependee" list from example 3. If a node sets another node as a dependent of it, the target node stores the source node as a dependee (figure 15).

What will happen if node A calls node B's update? It would be incorrect to let B call A's update after already having been updated itself. We can prevent this by checking if A is already being updated, as shown previously in example 2. This flag is set to "on" as long as a node is updating its "dependent of" list.

So initially, this "dependent of" list doesn't seem very useful. We can, however, use it to solve circular dependencies. Let's extend our relationships: A is dependent upon B, and B is dependent upon C. A is C's dependee and C is also A's dependee (figure 16).

Our node will perform the following operations in its Update:

We will only update dependees if:

With this knowledge, let's try to solve our example.

Steps 4 through 7 are repeated until a set maximum number of iterations have been reached, or until one of the nodes has stopped being marked as dirty. As a result, the update ordering will be: C, B, A, (C, B, A, C, B, A).

Now we can see the reason for setting an extra dependency between node A and C. If B marks itself as "not dirty", then A will not be updated, although it is very well possible that A needed to be updated because of the change in node C.

We can do all of this work without the "dependent of" list, which saves us from using quite a few pointers. However, I still don't like the two drawbacks that were described in example 3 of the previous section (the possibility that many nodes will already have had their update called and need to be updated again because of changes in nodes they depend on, and that target nodes might be updated multiple times). The question is, which is more important to you: memory usage or performance?

If you don't feel comfortable setting the dependee-relationships by hand on top of processing the "dependent of" relationships, you could automatically generate all the dependee relationships. We already automatically add a dependee "back pointer" when adding a "dependent of" relationship, so we could also detect whether we have a cycle and replace the "dependent of" pointer with a "dependee" pointer in the other object. Again, take a look at the relationships in figure 14. You could do something like this (zooming in on the updating of the dependee list):

What's Next?

Until now I have mentioned collision detection and response only occasionally, and treated this a single node in the dependency graph. Although this might work, good integration of force-based systems is very complex. Force-based systems form a very unusual exception in the game loop: they are constantly rewinding in time, while the update mechanism is based on a fixed time step. Here's some food for thought:

3D animation packages are taking dependency graphs much further. They are used not only to update nodes in the correct order, but also to optimize the performance of nodes that don't need updating. The Maya SDK states that fully explaining how their dependency graph really works would require an extra manual. I believe them, and I would love to read such a manual.

Granted, 3D animation packages have more memory and CPU time to spend then our games usually do. But it's only a matter of time before PCs and consoles have enough memory and CPU power for developers to rely on dependency graphs for precise views of the data, rather than accepting the little flaws that we're currently okay with.

Acknowledgements

Thanks to Peter Verswyvelen for his insight on this subject.

______________________________________________________