Crashing into the New Year: Collision Detection

The last several years have moved at an incredible pace. It was a year with amazing advances in the visual quality of games. The predictions that 3D hardware would become a major force in the industry have come true.

Consumers can now buy cards for under $100 that deliver 3D graphics performance that would have cost thousands only a few years ago. This added processing power leaves game developers more and more time to dedicate to exploring other areas in computer simulation.

I’m continually amazed that learning a simple trick or technique can open the door to so many different effects and applications. In this article, I’m going to investigate the problem of collision detection. Collision detection is a huge issue in graphics simulation. In fact, it’s an active area of research, so SIGGRAPH and professional journals are a great source of information.

Let me start off by looking at some common problems that can be important to a variety of game applications. These routines, though fairly simple, are very handy to have in your library. The first issue is how to determine whether a point is inside an arbitrary area. Detecting whether a point is inside a convex polygon can be determined very easily. Figure 1 shows a point inside a simple four-sided polygon. Our first step is to create perpendicular vectors for each of the polygon edges and a vector from the test point to the first vertex of each edge. The perpendicular of a 2D vector can be created by simply creating the vector, swap the X and Y components, and then negate the X. As you may recall from previous columns, the dot product of two vectors defines the cosine of the angle between those vectors. If the dot product for each of the edges is positive, all the angles are less than 90 degrees and the point is inside the polygon. This is exactly analogous to a 2D version of backface culling for 3D polygons.

That rule is pretty useful for some things. However, it only works when the boundary that you’re checking is convex. Many spaces that we’re interested in are actually concave (Figure 2).

This polygon looks like a character in a Duke Nukem level. And in fact, Duke is a pretty good application for this kind of test. Each "sector" of a Duke level is a polygonal boundary defining a region with a specific floor and ceiling height. Knowing whether I’m inside or outside of a particular sector is important information. Unfortunately, the aforementioned dot product test won’t work on these concave polygons. I could divide this region into smaller convex polygons, but that wouldn’t be very efficient. Luckily, this problem is the classic "point in polygon" test that’s commonly described in computational geometry books. There are many approaches to solving this problem, but I want to look at just two of them.

Here We Go Round the Vertex List

One method for determining if the test point is inside the concave polygon comes from the idea that a circle is 360 degrees. Calculate the angle between each vertex and the test point (at the test point itself) and then add up all the angles. If the total is equal to 360, then you are inside. You can see what this looks like in Figure 3.

This actually works very well, however, it is not very efficient. Calculating each angle requires a dot product and an arccosine operation. Those will add up quickly.

A better strategy is to divide the polygon into quadrants centered on the test point, as in Figure 4. Start at the first vertex in the polygon and set a counter to 0. Anytime an edge crosses from one quadrant to the next, add one to the counter if it crosses clockwise around the test point and subtract one if it crosses counter-clockwise. If the edge crosses diagonally across two quadrants, you need to determine which side of the test point it crossed, and then either add or subtract 2. Try it yourself on Figure 4. Start at vertex 1. Add 1 when edge 3-4 crosses from quadrant I to II, and subtract it again with edge 4-5. When you reach the last edge (11-1), you should have 4. When using the routine, if the counter is equal to 4 or –4, the test point is inside the polygon. You can see the code for this routine in Listing 1.

Listing 1. The Quadrant Approach
to the Bounding Box Test

// FIGURE OUT WHICH QUADRANT THE VERTEX IS RELATIVE TO
// THE HIT POINT

#define WHICH_QUAD(vertex,hitPos) \
( (vertex.x > hitPos->x) ? ((vertex.y > hitPos->y)
? 1 : 4) :( (vertex.y > hitPos->y) ? 2 : 3) )

// GET THE X INTERCEPT OF THE LINE FROM THE CURRENT VERTEX TO
// THE NEXT

#define X_INTERCEPT(point1, point2, hitY) \
(point2.x - ( ((point2.y - hitY) * (point1.x - point2.x))
/ (point1.y - point2.y) ) )

/////////////////////////////////////////////////////////////
// Procedure: PointInPoly (SUM OF ANGLES CROSSING VERSION)
// Purpose: Check if a point is inside a polygon
// Returns: TRUE if Point is inside polygon, else FALSE
/////////////////////////////////////////////////////////////

BOOL CFateView::PointInPoly(tSector *sector, tPoint2D *hitPos)
{

/// Local Variables /////////////////////////////////////////
short edge, first, next;
short quad, next_quad, delta, total;

/////////////////////////////////////////////////////////////
edge = first = sector->edge;
quad = WHICH_QUAD(m_edgelist[edge].pos, hitPos);
total = 0; // COUNT OF ABSOLUTE SECTORS CROSSED
/* LOOP THROUGH THE VERTICES IN A SECTOR */
do {
next = m_edgelist[edge].nextedge;
next_quad = WHICH_QUAD(m_edgelist[next].pos, hitPos);
delta = next_quad - quad; // HOW MANY QUADS HAVE I MOVED

// SPECIAL CASES TO HANDLE CROSSINGS OF MORE THEN ONE
//QUAD

switch (delta) {
case 2: // IF WE CROSSED THE MIDDLE, FIGURE OUT IF IT
//WAS CLOCKWISE OR COUNTER
case -2: // US THE X POSITION AT THE HIT POINT TO
// DETERMINE WHICH WAY AROUND
if (X_INTERCEPT(m_edgelist[edge].pos,
m_edgelist[next].pos, hitPos->y) > hitPos->x)
delta = - (delta);
break;
case 3: // MOVING 3 QUADS IS LIKE MOVING BACK 1
delta = -1;
break;
case -3: // MOVING BACK 3 IS LIKE MOVING FORWARD 1
delta = 1;
break;
}
/* ADD IN THE DELTA */
total += delta;
quad = next_quad; // RESET FOR NEXT STEP
edge = next;
} while (edge != first);

/* AFTER ALL IS DONE IF THE TOTAL IS 4 THEN WE ARE INSIDE */
if ((total == +4) || (total == -4)) return TRUE; else return FALSE;
}

Don’t Cross that Line

The quadrant method is pretty efficient. However, there’s a completely different approach. An interesting feature of this problem can be found if you draw a line from the test point to a point definitely outside the polygon. Now count how many polygon edges crossed that line. If that number is odd, the point is inside the polygon. If the number of edge crossings is even, the point is on the outside. Try it out.

I saw a pretty fast way to implement this in Graphic Gems IV. This method projects a line from the hit position along the x axis. Only testing line segments that are on either side of this position lets you avoid some calculations. Segments that could cross this line require an x intercept calculation to be sure. However, this can be simplified to eliminate a divide because of the unique needs of the test. The code for this routine is in Listing 2. Whether or not this method is faster than the quadrant method depends greatly on the polygon being testing. The routines are so easy to implement that you should try both in your application if speed is a real issue.

Listing 2. The X Intercept Calculation.

// Procedure: PointInPoly (EDGE CROSSING VERSION)
// Purpose: Check if a point is inside a polygon
// Returns: TRUE if Point is inside polygon, else FALSE

BOOL CFateView::PointInPoly(tSector *sector, tPoint2D *hitPos)
{
// Local Variables
short edge, first, next;
tPoint2D *pnt1,*pnt2;
BOOL inside = FALSE; // INITIAL TEST CONDITION
BOOL flag1,flag2;

edge = first = sector->edge; // SET UP INITIAL CONDITIONS
pnt1 = &m_edgelist[edge].pos;
flag1 = ( hitPos->y >= pnt1->y ) ; // IS THE FIRST VERTEX OVER OR UNDER THE LINE

/* LOOP THROUGH THE VERTICES IN A SECTOR */
do {
next = m_edgelist[edge].nextedge; // CHECK THE NEXT VERTEX
pnt2 = &m_edgelist[next].pos;
flag2 = ( hitPos->y >= pnt2->y ); // IS IT OVER OR UNDER
if (flag1 != flag2) // MAKE SURE THE EDGE ACTUALLY // CROSSES THE TEST X AXIS
{
// CALCULATE WHETHER THE SEGMENT ACTUALLY CROSSES THE X TEST AXIS
// A TRICK FROM GRAPHIC GEMS IV TO GET RID OF THE X INTERCEPT DIVIDE
if (((pnt2->y - hitPos->y) * (pnt1->x - pnt2->x) >=
(pnt2->x - hitPos->x) * (pnt1->y - pnt2->y)) == flag2 )
inside = !inside; // IF IT CROSSES TOGGLE THE INSIDE // FLAG (ODD IS IN, EVEN OUT)
}
pnt1 = pnt2; // RESET FOR NEXT STEP
edge = next;
flag1 = flag2;
} while (edge != first);
return inside;
}

Standing at Arm’s Length

The above routines are enough to let your player navigate around in a Doom-style level. You would just need to make sure that the player is always inside a sector. If the player leaves one sector and does not enter any other, a "collision" has happened. This works very well. However, using the inside polygon test for collision by itself has a drawback. The player can get very close to the wall of a sector and still be considered "inside." Logically, this works fine. However, in a 3D rendered game engine, being too close to a wall is a bad thing. Textures will look blocky, they can distort badly, and walls may clip out.

What you really want to do is keep the walls at "arm’s length" from the player. You can simply make the logical collision walls closer in than the visual walls; however, this can lead to other problems. So how do I keep the character away from the wall? Turn once again to our dear old friend, the dot product. Take a look at Figure 5.

What I want to know is, how far away is the test point, t, from line segment A. An easy solution would be to find the nearest point, n, to the test point on the line segment and measure the distance to it. First, I create a vector, B, from the test point, t, to vertex p1. I can dot this vector with the line segment A. This will give me the cosine of the interior angle. If this angle is 90 degrees or greater, the nearest point is the vertex itself and I’m done. But let’s say that the dot product gives me 0.7, or the cosine of about 45 degrees. I will then do the same thing on the other side. I create a vector C and dot it with the segment A. If it had returned an angle greater than or equal to 90 degrees, point p2 would be the closest and I would be done again. In this case, the dot product returns 0.75, or the cosine of about 40 degrees. Now that I have the two dot products, a linear ratio will solve the problem.

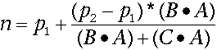
You can see the code that determines the nearest point on a line segment to an input point in Listing 3. The squared distance from t to n can be used to make sure the player cannot get too close to the wall. When I combine this with the inside-polygon tests, I have the pieces I need to create a Doom-style collision model. In these days of Quake III and Unreal, it may seem a bit retro to talk about Doom-style collision detection. However, the ability to build simple collision boundaries that you can use and modify in real-time is a very attractive feature. Rules in game development are meant to be broken. Just because these days you are displaying a world made of 3D polygons, your collision boundaries don’t have to be 3D polygons. Many of the environments we wish to interact with have boundaries that can easily be defined as 2D concave-polygonal-line-segments. Sometimes the best results can be achieved with simple solutions. If you didn’t have these routines already in your math library, add them and you will be surprised by how often you use them.

Listing 3. Finding the Nearest
Point on a Line Segment.

// Procedure: GetNearestPoint
// Purpose: Find the nearest point on a line segment
// Arguments: Two endpoints to a line segment a and b,
// and a test point c
// Returns: Sets the nearest point on the segment in nearest

void CFateView::GetNearestPoint(tPoint2D *a, tPoint2D *b,tPoint2D *c,tPoint2D *nearest)
{
/// Local Variables ///////////////////////
long dot_ta,dot_tb;

// SEE IF a IS THE NEAREST POINT - ANGLE IS OBTUSE
dot_ta = (c->x - a->x)*(b->x - a->x) + (c->y - a->y)*(b->y - a->y);
if (dot_ta <= 0) // IT IS OFF THE AVERTEX
{
nearest->x = a->x;
nearest->y = a->y;
return;
}
dot_tb = (c->x - b->x)*(a->x - b->x) + (c->y - b->y)*(a->y - b->y);
// SEE IF b IS THE NEAREST POINT - ANGLE IS OBTUSE
if (dot_tb <= 0)
{
nearest->x = b->x;
nearest->y = b->y;
return;
}
// FIND THE REAL NEAREST POINT ON THE LINE SEGMENT - BASED ON RATIO
nearest->x = a->x + ((b->x - a->x) * dot_ta)/(dot_ta + dot_tb);
nearest->y = a->y + ((b->y - a->y) * dot_ta)/(dot_ta + dot_tb);
}

Colliding in the Third Dimension

Running around a maze is one thing, but that’s just the beginning to the collision detection story. Consider the problem of determining if two objects have collided. Two of the most common approaches to this problem are bounding boxes and bounding spheres. For a bounding sphere, find the point furthest away from the center of the object. The distance of the point from the center defines the radius of the bounding sphere. You can see a bounding sphere around an object in Figure 6. Now imagine that the object and circle around it are actually 3D. As you can see, although the entire object is inside the sphere, it isn’t a snug fit. You can see how easy it would be to have an object that would hit the bounding sphere yet miss the object completely.

So why use a bounding sphere? Well, testing to see if a collision has occurred is really fast. If you measure the distance between two objects, and the distance is less than the radius of either bounding sphere, then there is a collision. This is a very quick test, so it’s easy to see why many games use spheres as at least a first line of defense. But if you need to determine exactly where two objects made contact, this won’t be enough.

Axis-aligned bounding boxes, or bounding boxes for short, are another simple method for collision detection. The box is called axis-aligned because the sides of the box are parallel to the principle world x, y, and z axes. This reduces the check for collision to a simple minimum-maximum test. You create the box by determining the minimum and maximum extents in each dimension. The collision test then consists of:

IF ( (point.x >= box.minX
and point.x <= box.maxX)
and (point.y >= box.minY
and point.y <= box.maxY)
and (point.z >= box.minZ
and point.z <= box.maxZ)
)then a collision occurred.

Bounding boxes are a simple, fast way to check for rough collisions. However, like the bounding spheres, the fit is not necessarily very accurate. They’re generally used as a first test to check if further investigation is needed. You can improve the fit by maintaining a hierarchy of smaller bounding boxes or spheres that are tested after the initial collision is determined. For many games, such as 3D fighting games which require fairly detailed collision, this is enough for realism. If you need more detailed collision information, you need to look elsewhere. Other methods such as oriented bounding boxes (OBB), where the bounding box is allowed to rotate to an arbitrary orientation, will allow for a tighter fit than either above method. However, even OBBs do not provide information on the exact point of collision on an arbitrary mesh unless the object happens to be a box.

Getting to the Point

If you really need to know which point of an object has collided with another — say for your realistic physics simulation — you have some work in front of you. All the other techniques are good first steps, and serve to filter out unneeded calculations. I’m going to start out in 2D again to make things easy. Let me begin by considering only convex objects. Remember that convex objects are polygon meshes that contain no interior angles greater than 180 degrees. Figure 7 outlines the problem.

I am interested in deciding whether polygon 1 is colliding with polygon 2. I could use my point-in-polygon test from earlier, and test every point in each polygon and see if it’s in the other. That wouldn’t be very efficient though, and in 3D it would be even less reasonable. What I really want to find is a single feature that makes it impossible for polygon 2 to be inside polygon 1. It turns out that if I can find a line that separates the two polygons, then they cannot be colliding. To make it easier, I will use the edges of each polygon as a test line. If all the vertices of polygon 2 are on the other side of an edge in polygon 1, they aren’t colliding.

You will recall from the convex point-in-polygon test that I used the dot product to determine if a point was inside an edge. I can use the same test to see if a point is outside. In other words, if vectorba dot vectorbc < 0, then point c is outside of polygon 1.

That dot product operation sure comes in handy. In 3D, you would be dotting the face normal with the test point, but it works out similarly. The first time you test to find this separating edge, you need to test all edges in each polygon against all the vertices in the opposite one. However, once you have found a separating edge, you can store this information so that edge is the first one you will test the next time you try. This caching of collision points can speed up testing quite a bit, and I highly recommend it.

That is all the time I have for this month. Next month, I will examine what exactly is required for detecting the collision point in 3D. I will also discuss what you can do with this information once you have it, and work out some cool samples to demonstrate it.

For Further Info:

• O’Rourke, Joseph. Computation Geometry in C. Cambridge University Press, 1993. A very good discussion of point-in-polygon strategies as well as path finding and convex hull operations (hint: may be handy).

• Heckbert, Paul S., Editor. Graphic Gems IV. Academic Press, 1994. Inside polygon strategies and routines.

• Baraff, David, and Andrew Witkin. "Physically Based Modeling," SIGGRAPH Course Notes, July, 1998, pp. D32 – D40. Collision detection and response methods.

Jeff Lander made a resolution this year to shrink his own bounding box and to spend more time away from the computer. Show him how futile this is by mailing him at [email protected].