Author: by Nassib Azar

Introduction

Game spaces provide a context for the game's rules and systems, and a space for the game agents to perform mechanics. When we go about designing game spaces, sometimes thinking in pure spatial terms clouds what a designer needs to achieve with a certain game space.

For FPS games, sitting yourself down with your favorite prototyping tool kit and drawing corridors and rooms is a recipe for disaster. It is difficult to design interesting spatial puzzles when you are creating game spaces using the rules of reality. How many office blocks are fun to navigate?

Molecule design is a way of applying graphing theory for concepting and fine-tuning of various types of game spaces. This rational approach to design is a means to design spaces without thinking about the representational elements of space itself. This article still accepts the importance of planar maps; however, we need better tools to help us create these first.

This article will examine some useful tools gathered from the field of graphing theory that designers can use to conceptualize various game components. The latter half of this article will examine a real-world application of these tools. By doing so, we will examine how iterations of a level design benefited from this abstracted means of realizing space.

The Basics of Graphing

Graphing theory is a broad and diverse field of mathematics; however, this article discusses graphs that can explain spatial relationships. Core to graphs that explain spatial relationships are nodes and edges (Figure 1). Nodes can represent game spaces / rooms, pickups, spawn points and AI pathing nodes. Edges define relationships between nodes.

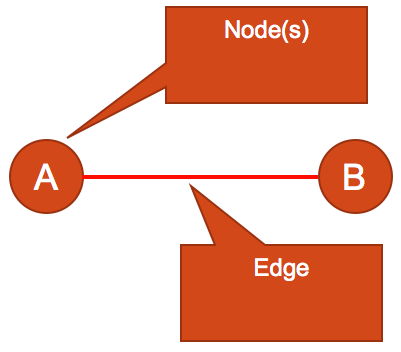
Figure 1

Figure 2 is a simple molecule consisting of several nodes, linked by edges. In this example, we have defined a set of tokens around the players spawn point. This is a literal depiction of space using a graphing approach. Nodes become linked by edges, and these define the shortest possible distance between the player and other node. The more powerful a token is, the longer the edge should become.

This approach works well for PvP games -- to create a game space with roughly similar distributions of pickups, to achieve game balance. Repeating and rotating a molecule leads to symmetrical distributions throughout the game space. Edges are abstract ways of defining relationships but not necessarily hallways or any other level geometry. To explain this further, we need to look at weighted and directed graphs.

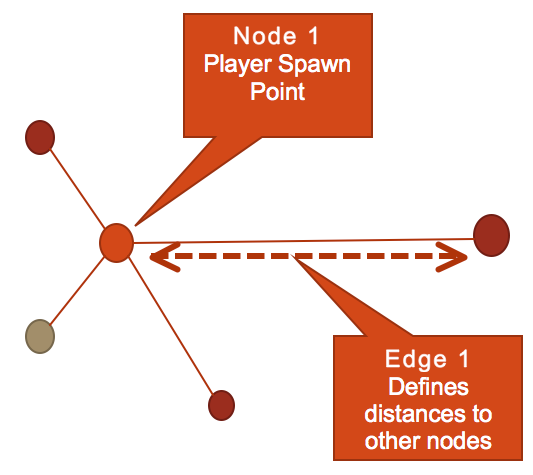
Figure 2

We can manipulate the physical appearance of our edges to help communicate different types of relationships between the nodes. In Figure 3, the edge between nodes A and C is thicker than the rest. If we are using graphing theory to create spaces, and the nodes represent particular game spaces, then the larger edge does not imply a bigger space between the two nodes, but rather a more direct route.

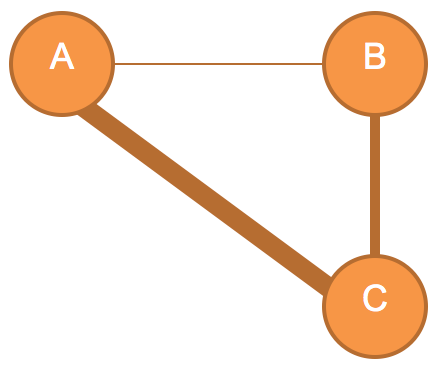
Figure 3

Figure 4 takes our molecule from Figure 3 and uses weighted edges as a guideline to place out level geometry. In this example, heavy weighted edges create a path between nodes A and C that is direct and unimpeded. Alternatively, the thin edge connecting nodes A and B results in a meandering pathway that is complex in nature. This example shows that edges do not depict geometry, but rather the relationship between nodes.

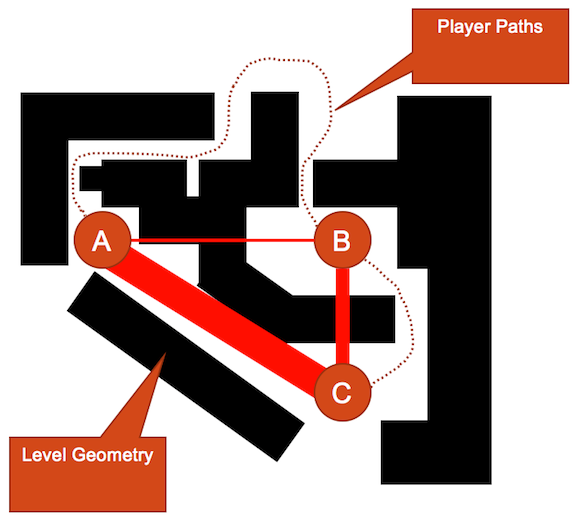
Figure 4

We can further increase the information that an edge communications by adding direction. Figure 5 is an example of a graph that has directed and weighted edges. Figure 5 uses directed and weighted edges to communicate two different ways to get between node A and node B. The thicker edge is more direct than the other. Linking nodes B and C is an indirect one-way gate. The thick edge linking nodes A and C is another one-way gate. The thickness of this edge shows a direct and unimpeded relationship between the nodes.

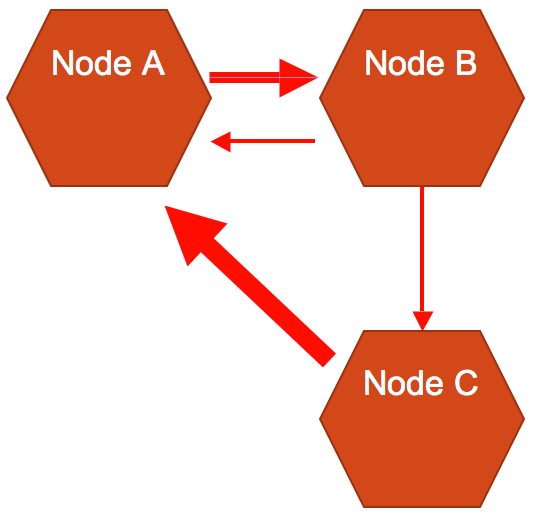
Figure 5

Nodes and edges can represent nearly any feature of game level design. For example, we could use a system whereby the weight of the lines also tells us about the difficulty of getting between nodes. By using edges to depict vertical space, we could say that node C is the highest point of the map. Node C is then transitive in the sense that it can only be accessed from node B. The one-way direction between nodes B and C might be achieved by having a "jump pad" at node B, pointing towards node C, but not in the opposite direction. It is really at the discretion of the designer and their team to define a key for their particular molecule system.

To further explain the concept of using spatial molecules to create play spaces, let us consider one example molecule and how it should and should not be implemented. The molecule represented in Figure 6 is a simple spatial molecule that defines a linear level progression, suitable for single player type maps. Weighted edges have not been used in this example; however directed edges have been used to create interesting spatial puzzles.

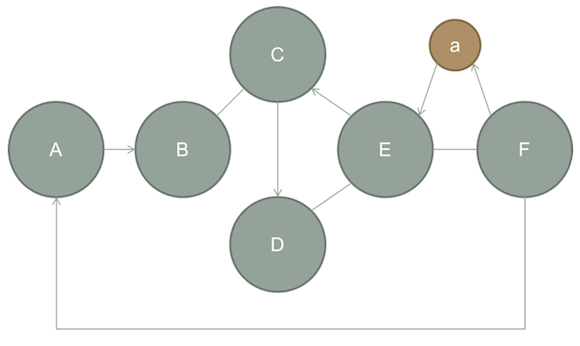
Figure 6

Figure 7 is an example of what not to do with a spatial molecule. The reason to use a molecule-based approach is to free your creative process from thinking in purely spatial terms, and instead think about creating interesting spatial relationships. Although the planar map in Figure 7 does follow the spatial relationships of the molecule, it is a boring, linear space.

There are also a number of other flaws that demonstrate why designing maps from a planar perspective is problematic. First, the linear, room-by-room layout of the map is a direct product of drawing maps out in planar space. When your imaginative space is two-dimensional, your maps will be two-dimensional also. As such, there are no interesting vertical spaces and, more importantly, the objective is not clearly visible from the beginning of the map.

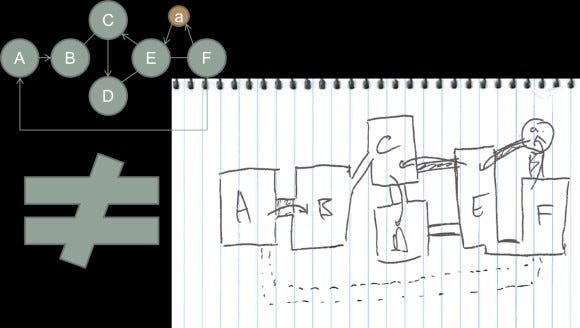
Figure 7

Figure 8 is a better implementation of the same spatial molecule. This example treats each node as a "play space" and uses the edges of the molecule to define how these play spaces can interact with each other. Below is a hypothetical playthrough:

In this example, the player starts on a ledge overlooking a valley (node A). Beside them they can see play area F, a large manmade structure towering over the environment. This is the final objective and its size and scale immediately compels the player to wonder how they can get inside the structure. The player notices that the entry to the tower is locked, but they can see another structure in the distance, a large pyramid in section E of the map. The pyramid has a grand entryway that draws the player's attention -- it is the only other major point of interest in the landscape and as such acts to draw the player towards it.

Between their starting point at section A and the pyramid, the player sees a number of obstacles that they need to overcome: a large wall, a bridge with a closed gate and a canyon filled with water. The player has time to survey the landscape from their elevated position and gain situational awareness. From node A the player begins to plan their route.

The player jumps down from the elevated platform of node A -- this is a one way gate. In section B, they need to make their way to the open gate. Initially they will be drawn to the bridge that crosses the canyon, but they soon realize that it is blocked off and can only be open from the other side. Close to the bridge, the player notices that there is a section of rocks which they can use to jump into the river below without taking damage.

Once in the river, they follow it downstream towards a large open section. Here the player finds a set of stairs that will take them up to the plateau containing the pyramid. Once inside the pyramid, there is an underground road which links back to the objective at section F. This road will collapse behind them once they get close to section F so it acts as a one-way gate.

The hidden room, "a", is connected to F and to E, however it is also a one-way gate and can only be accessed from F. The room will flood once entered, causing it to be blocked off from F, and forcing the player back up into section E.

Section F is the objective, and once inside, the player can continue onwards. Note that because section A is a one-way gate and section F is closed off, the player should not be allowed to return back into the open-area space.

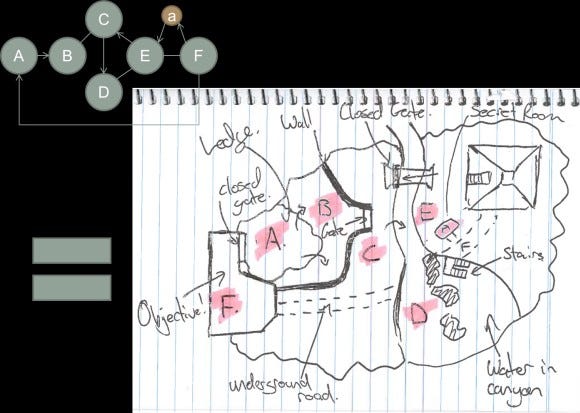
Figure 8

Figure 9 is another interpretation of the same molecule, this time using a more traditional room-based approach.

In this playthrough, the player starts in section A, a large room with two doors, one open and one closed. The player goes through the only open door into a large arena section -- B. There is a door in this room, but it is blocked in such a way that the player knows that it is broken and they cannot get through it. Inside B are a number of containers that the player needs to jump between in order to get out of the room.

Above this tall room is a gantry, suspended high above the floor. The player can also see a room overlooking the arena -- section E. The player jumps from container to container, slowly exploring the vertical space. Once they are in the highest position they enter a network of small service tunnels (section C) that gradually descend.

After navigating the tunnels, the player drops down into an outdoor section -- section D. From here, they can go between D and E via the stair. Once inside E, they can cross the suspended bridge that they saw earlier to their objective. On the way to F, they notice a pickup, situated on a container that they previously could not access via section B. If they player decided to jump down onto this container, then they need to backtrack via, B, C, and D.

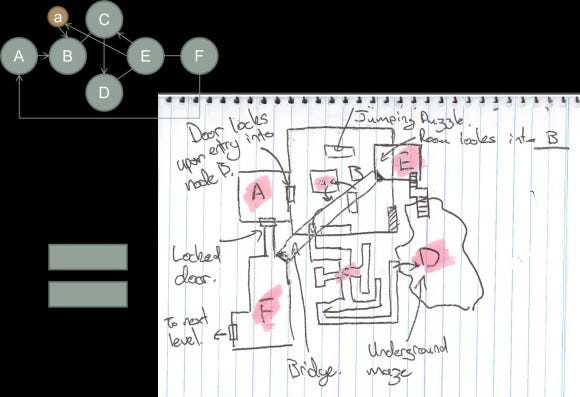
Figure 9

Figure 8 and Figure 9 demonstrate how creating a planar map based on a molecule can be an excellent way to creatively problem-solve spatial design. This method of concepting forces the designer to create interesting spatial options at the planar map stage of level design. From my own experiences, designing levels starting at the planar stage more often than not leads to boring, linear progressions which are a consequence of trying to create interesting 3D spaces in a purely 2D creative space.

More Advanced Toolsets

Now that the basics of graphing theory have been discussed, it is time to move on examine some of the tools that designers have at fingertips when going about designing game spaces. It is important to note that these are just some of the concepts available for designers. As this article is appropriating some of these ideas, there are instances where it is necessary to deviate from some of the pure mathematical interpretations of these concepts. This article will explore the following graphing concepts:

Dominion / Domination Theory

Domination Theory is a way to understand how nodes can have an area of effect (AOE) and how this AOE might overlap with other nodes. This tool is especially useful to analyze your existing maps from the perspective of player experience. Using this method, each node represents "zones of play" and the intensity of play that happens within each space.

This notion of "zones of play" is something that was originally explored during the design of Half-Life and is referred to as "Experiential Density." Experiential Density is a term coined by Valve's designers during the creation of Half-Life. The concept refers to play experience being distance-based, rather than time-based. The basic concept is that a player should always opt-in to the next section of the play experience. They should be given as much time as they need in order to accumulate loot or simply explore before being placed in a situation of high intensity.

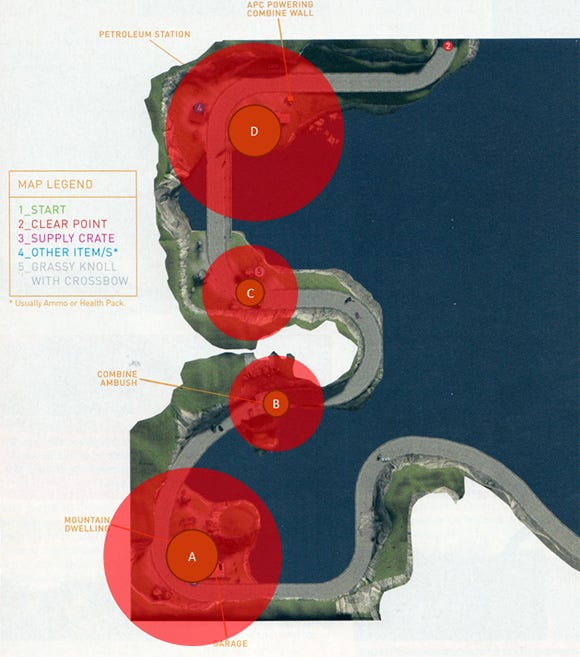
Figure 10

Figure 10 is an example taken from Half-Life 2 that demonstrates how dominion theory can be used to promote Experiential Density. In this map, we have three distinct section of high-intensity play represented by nodes, A, B, and C. The area of effect around the nodes is meant to represent the intensity of play in each of these sections. The greater the AOE, the greater the challenge posed to the player.

If we are designing with Experiential Density in mind, then we can use Dominion to ensure that we are not forcing the player into consecutive, high intensity play zones. Quite literally we are looking at molecule design to ensure that we have enough emotional "cool-down" time for the player between zones. I like to think of these cool-down zones as being similar to dynamics in music. In his book The Clarinet and Clarinet Playing, musician and author David Pino sums this notion up well:

Think of it this way: If you look out from the shore upon a great expanse of ocean, you may become very quickly bored. If however the ocean is enlivened by the sudden appearance of an interesting ship, the view is more likely to hold your attention. Similarly, if your view is suddenly filled with hundreds of ships, not any single one of them will hold interest for very long. The same principle holds for the performance of music: If the listener perceives no subtleties he becomes bored; if he detects nothing but subtleties he becomes disorientated and bored... the most important element in any piece of music is its rhythmic flow.

To better demonstrate how Dominion Theory works, let us use the same example from Half-Life 2, but let's intentionally break the Experiential Density (Figure 11). In Figure 11, the overlapping play sections are represented by the overlapping, red AOEs. From a player experience perspective, this is like trying to read a book with no punctuation. The game experience lacks a satisfactory blend of emotional states as the player "detects nothing but subtleties," in Pino's words.

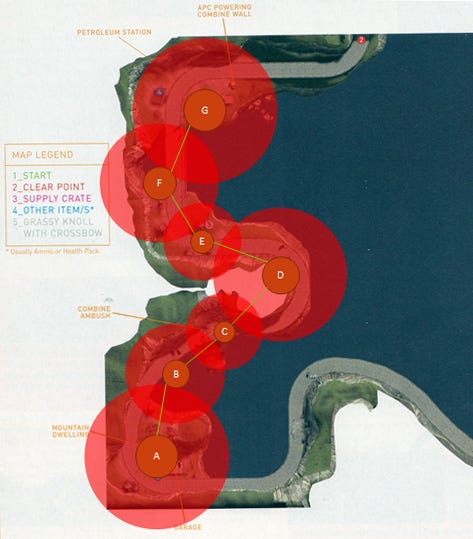
Figure 11

This map, therefore, is a prime candidate to apply dominion theory to in order to solve the problem of Experiential Density. Depending on the amount of cool-down space you wish the player to have you can adjust your rules for "dominion-overlap" to suit. For example, you could remove overlapping nodes from your molecule so there was no-overlap (as per Figure 10) or you could revise your zones of play so that the play intensity is lower, yet more frequent (as in Figure 12).

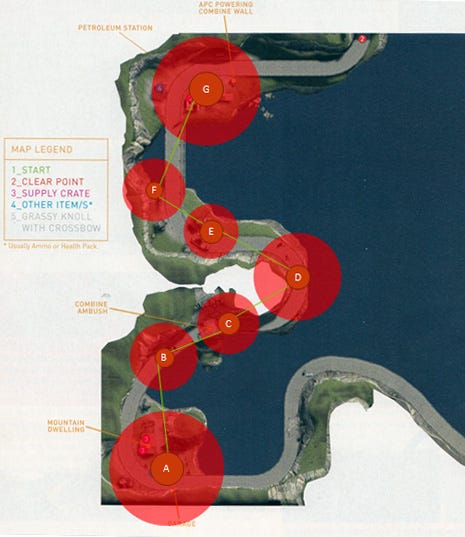
Figure 12

From a level concepting perspective, Dominion can also be used to define a "spawn exclusion zone" or any other type of "exclusion zone." An exclusion zone can define an area in which something should not happen -- i.e., there should not be an overlap with the dominion of another node. In this application of Dominion Theory, a node can represent a pickup or a player spawn point. The red AOE is therefore a visual representation of the spatial metric that you have decided to use to represent minimum distances to a spawn event.

Figure 13 is an example of using Dominion to define an exclusion zone. The node represents an actual player spawn point, but could be any game token. The red AOE around the node is a visual representation of the minimum distance that another spawn can occur. For example, if we are working within the confines of UDK, then we might say that based on the size of our map, each spawn point must be at least 1024UU away from another if it occupies the same vertical space. The rules of your dominion zones are flexible; however, for this example, the rule is that no other spawns are to happen within the Dominion Zone -- at least from a planar perspective.

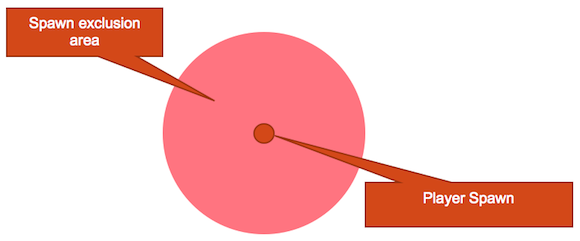
Figure 13

Figure 14 is a dominion problem that needs to be resolved. The problem may be a result of overlapping spawns or pickups that are too close. We can remove the overlap in dominion by placing these nodes further apart or by simply using level geometry to mitigate overlap, as in Figure 15.

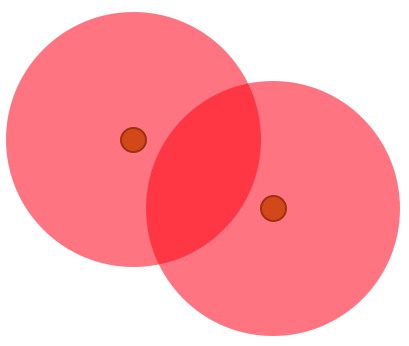
Figure 14

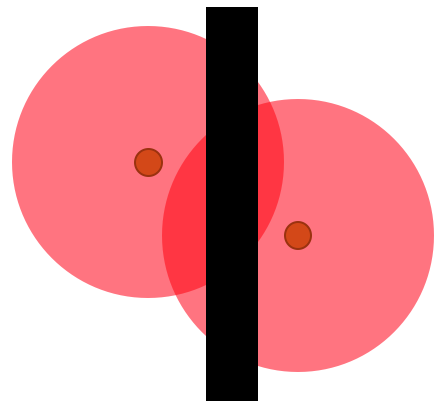
Figure 15

It is important though to use common sense when implementing Domination Theory. Once you start to add in level geometry, you are adding another layer of complexity to your designs that will call for revising some of your rules.

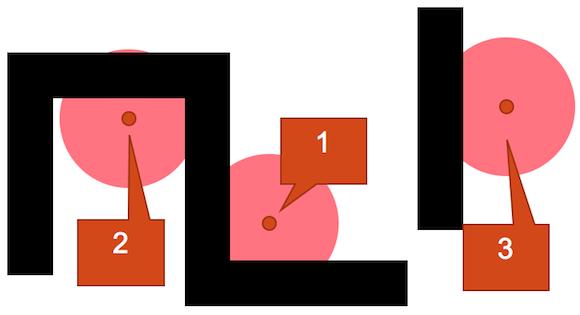
Figure 16

In this example, Figure 16, I have used the spawn exclusion system to spread spawn locations in an asymmetric environment. One thing to note is that spawn point 3 has been intentionally moved further away from spawns 1 and 2.

The reason for this is due to the fact that spawns 1 and 2 have fewer approach vectors -- i.e. the player can see any oncoming enemy in their view frustum upon spawn. Spawn point 3, on the other hand, has a wide arc of approach vectors which the player cannot possibly cover within the same view frustum, hence the need to compensate by moving it further away from the other spawn points.

You can apply this same spawn exclusion system to other pickups -- the more powerful the pickup, the larger the spawn exclusion should be. As mentioned earlier though, level geometry and other factors such as pickups and the player's ability to move within the game space will necessitate the use of more sophisticated analytical tools -- namely Spanning Trees and Steiner Points.

Using Graphing Theory to Understand Player Choice and Strategy

All game levels provide some type of spatial problem-solving puzzle. These puzzles take a number of forms, but one type of puzzle which can be improved via the application of graphing theory are puzzles relating to optimum movement strategies seen in all well-designed deathmatch style maps.

Players thrive on choice; however, too much choice can be just as bad as too little choice. Further to this, players take great pride in achieving victories via the execution of "good" strategic choices. So far we have used graphing theory to examine the construction of play spaces; however, graphing theory is especially useful when we examine our level designs with human cunning and strategy as our primary concern. The principles of Steiner trees, spanning trees, and maximum and minimum cutting are integral to understanding these human factors.

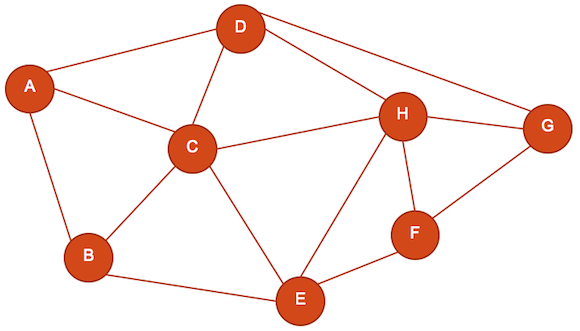
Figure 17

Figure 17 is an example of a hypothetical level. Each node, designated A-H, represents a different type of play space, and each edge represents how many different ways a player can move from space to space. Note that each edge does not represent a corridor, but rather the player's options. The length of the edge is short or long based on how complex that particular route is -- i.e., the longer an edge, the more time it should take to use that option. In the case of Figure 17, each space (node) has between three to five different options for the player to consider when exploring the space. The graph also communicates how the player needs to move through spaces in order to traverse the map.

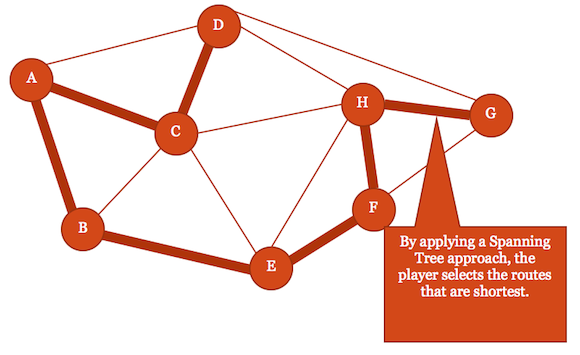
Figure 18

Spanning trees can be used to define the most optimal connection of nodes in a graph. This tool can also be useful when we are trying to understand player behavior in a map and look for aspects of the design that may be unfair or unbalanced. We can use spanning trees such as those seen in Figure 18 to help disperse item pickups, define spawn points, and place level geometry to help counteract any significantly overpowered (OP) movement strategies that might emerge in a PvP map.

Although mapping out specific permutations of the optimal movement strategy for a level is a good way to start defining your play spaces, it is essential that we give further consideration for players' desire to exercise cunning and emergence. A good example of this point is considering the pride that people (not just players) take in identifying shortcuts. A shortcut is a set of strategic choices that sit outside of the norm. Players will look for opportunities like this in any game environment and their discovery and exploitation of this can be very satisfying on an emotional level. A great way of planning for an understanding this behavior comes from the theory of Steiner trees.

A Steiner tree is a type of spatial problem that looks for the shortest interconnection between a number of nodes. The example that Raph Koster gives in his "Games are Math" presentation is a good way to understand the application of Steiner trees in games. In his presentation, Koster states "If you have three nodes and you need to create the shortest possible route between them, what is the shortest amount of edges required?" Koster states that most people will answer something similar to Figure 19.

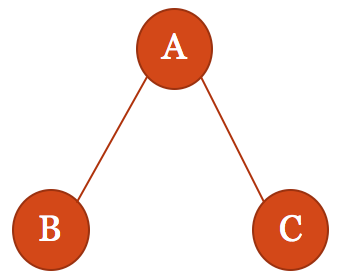
Figure 19

The answer to this problem is slightly more devious, as it requires adding another node in the puzzle -- a Steiner point. Via introducing the Steiner point in Figure 20, we have created the most optimal solution to this puzzle. Steiner points and the edges that they create can be treated just like any other type of graph. In the context of games, we can use weighted and directed edges to help define how a Steiner point might be a height element of a map or may be another one-way gate, like a teleporter or jump pad.

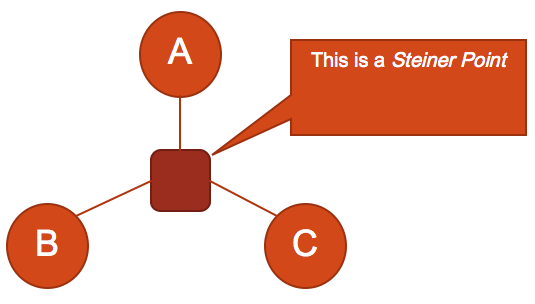
Figure 20

A Steiner Point is a shortcut. It is that element of a level's design that players will seek out in order to exploit. The secret for level designers is to make the Steiner points in your map seem less obvious than the spanning tree routes. Borderlands is a good example of this. Within the maps, spanning tree paths are clearly defined and for the most part, appear as clearly defined paths and gantries.

Steiner points exist within the game in the form of height elements which allow the player to skip large sections of the spanning trees by jumping down to certain parts of the map, therefore avoiding large path traversal. Krom's Canyon in Borderlands is just one example where the player can jump down from raised platforms to quickly move to another point in the map, therefore creating a Steiner point (see Figure 21).

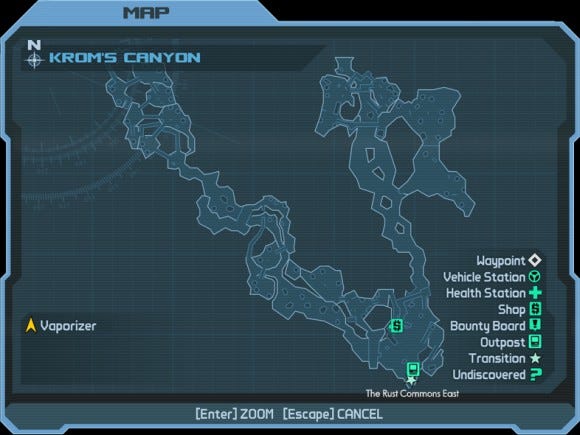
Figure 21

Figure 22 (taken from Krom's Canyon above) is an example of how spanning trees and Steiner points work from a level design perspective. In this example, in order for the player to get from node A to node F, they must enact a spanning tree solution. This relationship is represented in the level design by a set of gradually ascending platforms which are interconnected via bridges. A number of bonus items are implemented in this section of the map via Steiner points.

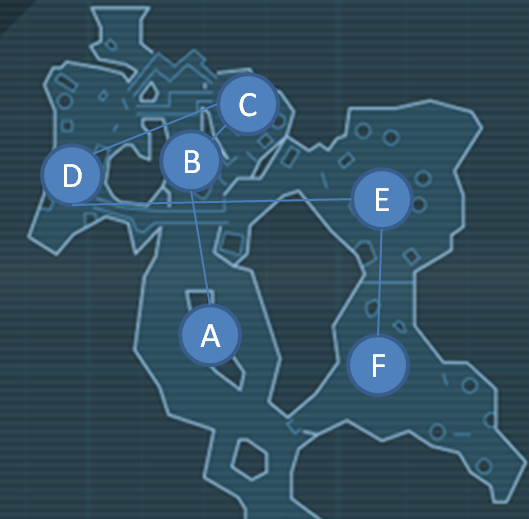
Figure 22

In Figure 23, two Steiner points have been added. Although there are actually several other Steiner points in this spatial molecule, these nodes are pickups placed on high platforms, only accessible from the nodes above them. As such, not only are these considered to be Steiner points as they offer the player a shortcut, but they are important points of interest for the player that allow them to explore the environment as a spatial puzzle.

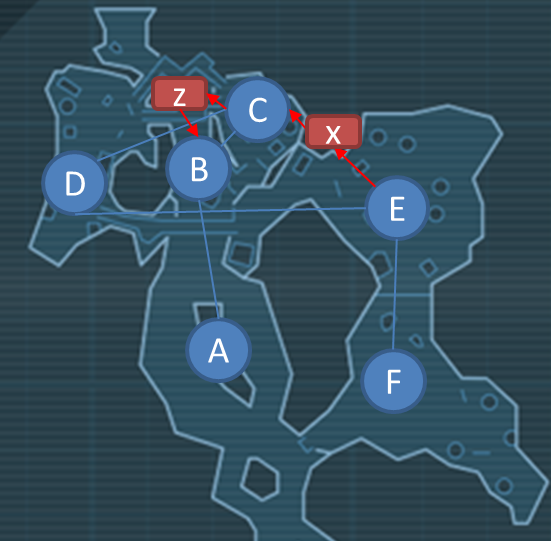
Figure 23

Figure 24 expands this particular section of play into an even more defined molecule and adds two other major Steiner nodes that show how the player can traverse the space when they are either ascending or descending.

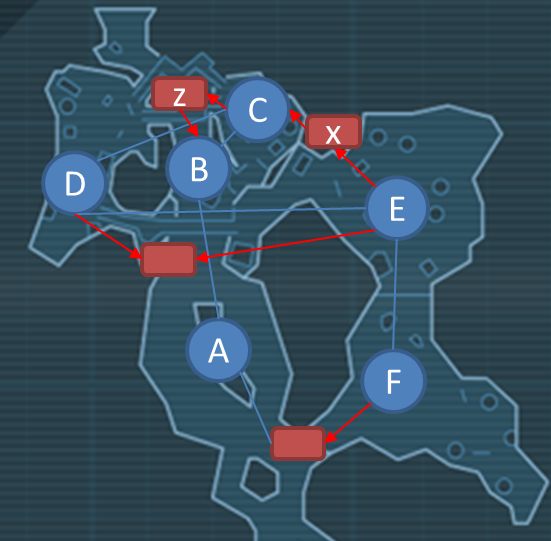
Figure 24

Now that we have taken a look at how Steiner points operate from a spatial puzzle perspective, lets revisit our spanning tree molecule originally introduced in Figure 17. If we applied Steiner points to link nodes in close proximity, then we would have something similar to what is seen in Figure 25.

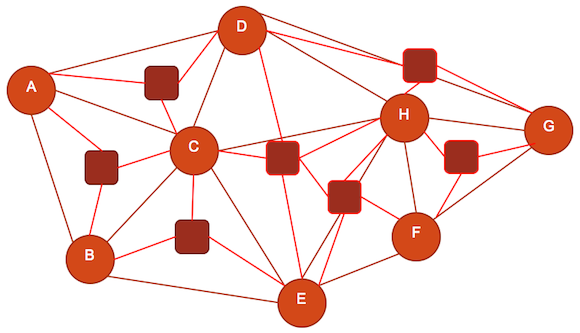
Figure 25

These Steiner nodes could take many forms. They could be teleporters, actual level geometry, or even height elements that allow for faster path traversal. Figure 25 shows how many Steiner points we could possibly have in this spatial design. According to Koster, too many Steiner points are bad for human players, because you have provided so much opportunity; there really isn't much scope to exercise what I like to call "skillful strategy." Basically, there is no pleasure to be derived from creating shortcuts in this environment because there are so many of them.

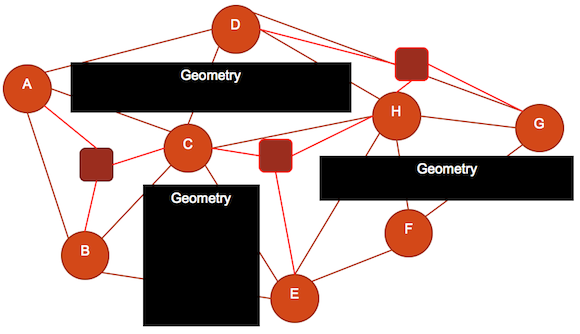
Figure 26

If we begin to use level geometry to reduce the amount of possible Steiner points, we are beginning to ask much more of the player. By giving them fewer options (Figure 26), we are asking the player to exercise better strategy than the other players on the map. The upside to this is that players who do well in this environment will take much more satisfaction from its successful completion, as they perceive the lack of options to be indicative of a more complex problem. To demonstrate how a reduction in Steiner points relates to increased difficulty, we need look no further than the Steiner tree problem that we see in the lower, east quadrant of the Fallout 3 overworld (see Figure 27.)

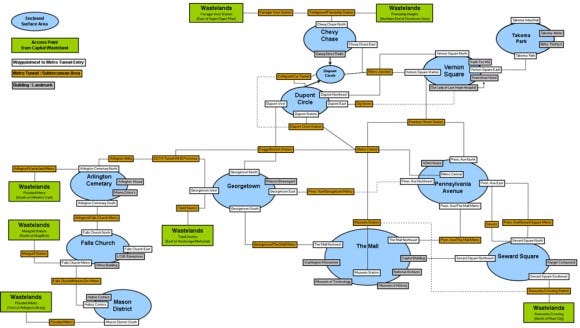
Figure 27

Spatial navigation problems in the early parts of Fallout 3 are negotiated via simple spanning trees where you have many possible Steiner points. This is most noticeable in the areas to the south of main Vault as this is the first (and easiest) part of the map that the player is expected to explore. As difficulty increases, though, these Steiner points are vastly reduced; this can be seen in the subway system of DC, which the player encounters later in the main quest of Fallout 3.

A Practical Implementation

So far we have examined the basic principles of graphing theory and applied this to the analysis of a number of commercial examples, but how does graphing theory stack up as a tool to concept game spaces? The following is an example of a practical implementation of the theory of molecule design created by Nassib Azar.

In this example, a molecule concept is tested, implemented, and refined in order to create a balanced, multiplayer space, which despite its simplicity, offers players with a significant amount of interesting strategic possibilities to explore.

The core idea Nassib decided to explore was a map design which had three layers of experience, represented as three concentric circles. The game space is a deathmatch style map within the default game type of Unreal Development Kit. The outer layer comprises low intensity zones designed to "feed" players into the innermost section of the game space.

For the purposes of this design, "intensity" is measured by the amount of players actively trying to kill each other within each zone. Figure 28 is one of the preproduction sketches of the map. This diagram explores how choke points, intersections, spawn points and weapon pickups could be used to increase the intensity of the play experience as the player nears the center of the map.

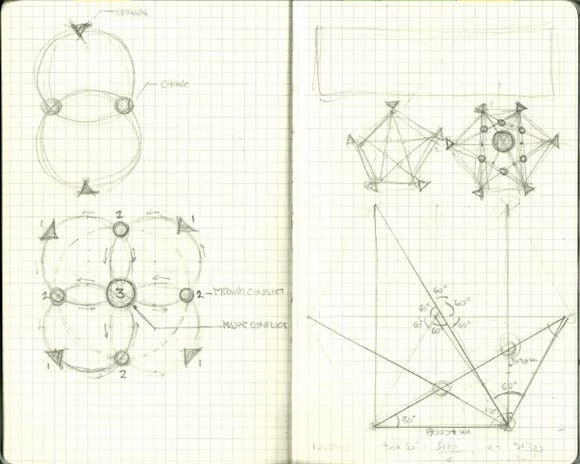
Figure 28

After some initial paper prototypes and feedback, the core idea of three concentric play spaces of varying intensity eventually developed into a more concrete molecule which defines the space as a whole. Figure 29 is an iteration of the early concept. In this iteration, we still have the same set of concentric circles representing intensity of play; however, edges have been added to describe how the outer sections feed into the middle.

To achieve this goal, Nassib applied the notion of Compression and Funnelling, a simple tool which looks at how forcing the player around a game space using various game elements can create heightened emotional states. In Figure 29, each edge represented additional vectors of compression on the nodes they led to. In the case of this example, the nodes represented spaces for conflict; the more the edges leading into a node the higher the compression on that node (and as a result, the higher the intensity of game experience). In this application, node size was used to represent increased compression, and subsequently, intensity of play.

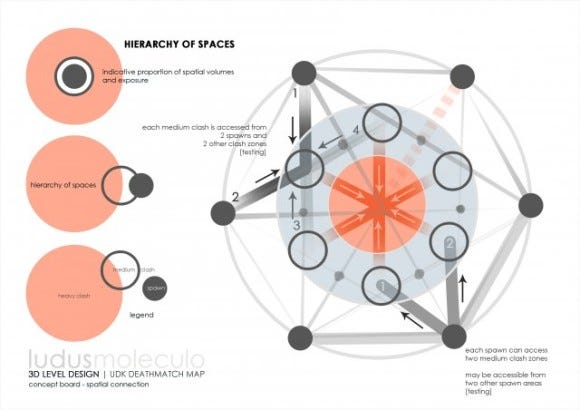
Figure 29

Although the application of molecule design is meant to create a distinction between play experience and level geometry, Nassib chose to explore whether pure geometrical representations of space have inherent player experience value. The hexagonal attributes of Nassib's molecule prototypes were worthy of further investigation. The question was: Would the molecule translate to actual level geometry and still retain the original design intent?

The prototype molecule used to define the overall game space went through a number of iterations in the form of grey box levels developed within UDK. It was clear through prototyping that the experiment had merit; the intensity of the player's experience increases as they work their way towards the center of the map. Nodes became generic play spaces (rooms) and edges became corridors that would feed into these spaces.

Figure 30 is one of the more advanced iterations of the grey box. It shows the implementation of the original molecule into a playable space. During testing, it was found that for intensity of play to increase, the room sizes needed to increase in order to accommodate the increased play intensity.

Room sizes are designed to create the most optimal zone sizes for the desired amount of play intensity. The original molecule design translated well in this regard. Play zones became progressively larger as they player moves towards the center of the map, yet the zones are also small enough to force the players into close proximity combat, hence increasing play intensity.

Figure 30

In order to create a syphoning of players towards the center of the map, a molecule was designed to aid in the placement of various weapon pickups. There are two main molecules used to define token placement. Weapon pickups were embedded in a molecule that forced the player to move quickly towards the center of the map. Health pickups were embedded in a molecule that forced the player to explore the circular boundaries of each play zone. The differing nature of these two molecules not only adds to creating clearly defined and different movement tactics for offensive and defensive play, but also aids spreading play over the entirety of the map rather than the central most zones.

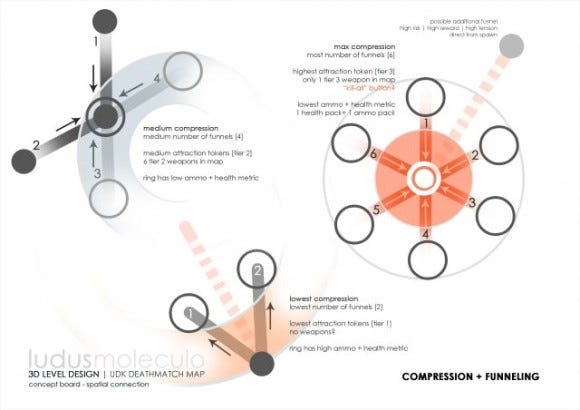
Figure 31 breaks down the graphing further. In the close up of the medium node (upper left), a differentiation is made between two different edge types leading into it. Edges 1 and 2 come from the spawn point while 3 and 4 are fed from other medium nodes. This suggests a difference in danger level and is therefore represented by expressing the edges differently. Although the initial design hypothesis suggested that there would be some type of discernable difference between edges one and two AND three and four, it took several revisions of the grey box to observe this hypothesis the real world, seen in Figure 32.

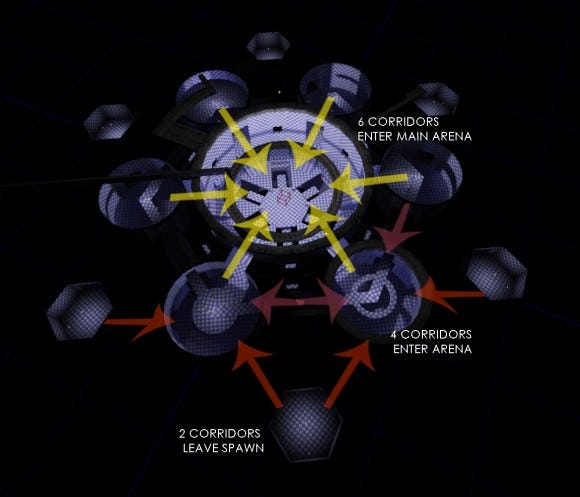
Figure 32

Early iterations of the grey box demonstrated a fundamental flaw in the design. Although play was becoming intensified as it reached the center of the map, a secondary mechanic was emerging; players became aware that it was possible to farm the outer ring of the map and rack up numerous spawn kills. As a result of testing, edges [corridors] 1 and 2 were raised to create one-way gates, allowing them to feed players into the map but not allowing players already within the map to access the spawn points. The elevated corridors were re-conceptualized in the physical space as maintenance shafts, as can be seen below in Figure 33.

Figure 33

The placement of pickups also benefited from the molecule design approach and followed a similar symmetrical layout to the level geometry. Although the use of symmetrical molecules creates an easy workflow for designing the map, too much symmetry is often boring and even confusing for players.

To address this issue, asymmetry was used to create navigation landmarks for the players as well rooms that highlighted different types of weapons and game mechanics. Differences in each room's layout served two purposes: to aid with player navigation and to create "perceived" advantages to each room. Perceived unfairness suggests no matter how fair or balanced a system is, players will be drawn to elements of the game that they believe are broken, even if they are not.

In essence, each room in the second ring contained a different type of spatial molecule. The molecules differed by varying choke points and cover elements. The result of this can be seen in the comparison between Figure 34 and Figure 35; both are rooms in the second ring and both offer different types of play experience within them.

Figure 34

After further iteration and testing, it was found that players were entering the primary room more than the second ring / medium rooms, but not at the expected proportion. The intensity of the play experience needed to be very high in the center room and there simply was not enough player traffic to achieve the desired experience. Of course, this could have been addressed with revising the space to make it smaller, however as much of the level art had already gone into production, it became necessary to look at alternative option.

To amplify this experience, a second ring of player spawn points where created on the mezzanine floor of the secondary ring. The walking distance to the center room from the upper spawns was shorter than the ground floor and therefore encouraged far more traffic to the central room and as such created the desired effect.

Figure 35

The two stacked spawns in Figure 36 did not have the same spawn-to-engagement times to the mid rooms. In other words, the edges above were not equal to those below when they should have been. By changing the position of the spawns in line with the revised molecule design, time to engagement was negligible when compared with the existing spawn points.

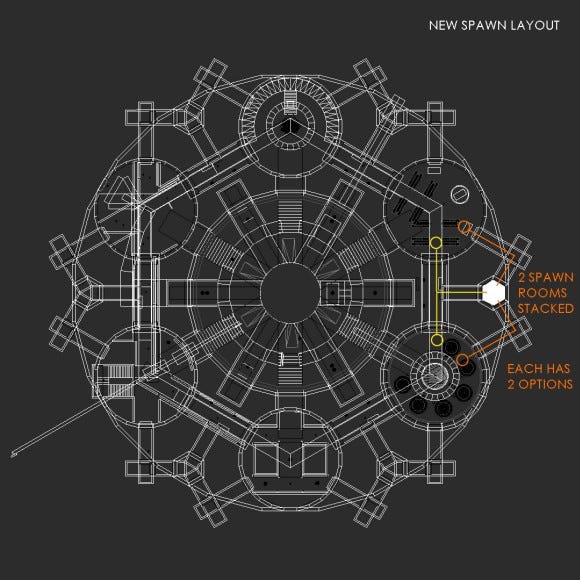
Figure 36

Symmetrical molecules create fair distribution of stairs and elevators in the map; however, the actual design of each of these three elevators is varied intentionally (Figure 37). The rationale for this approach was to highlight the psychology of perceived unfairness. Via testing, it was shown that most players thought that the stairs near their spawn point gave them the advantage, and that this advantage was not used against them. Asymmetry was also used in the design of stairs themselves, again this served two functions: to assist with navigation and vary the play experience in the medium rooms.

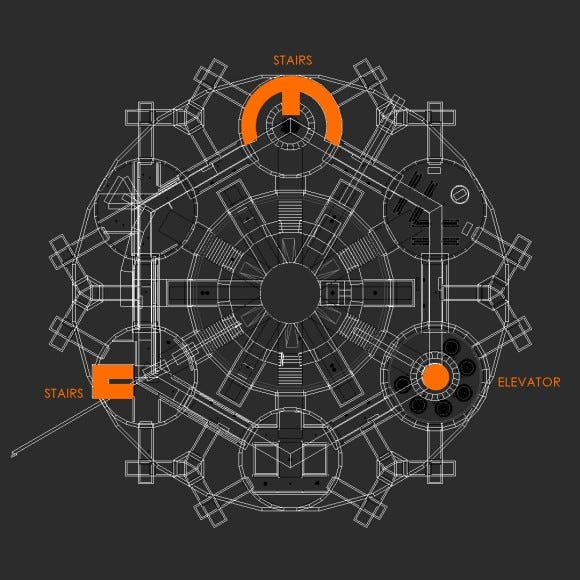
Figure 37

Another strategy that was used for balancing was not in the graphing theory itself, but highlights how graphing theory can help read player behavior. A Kismet script was created where every three minutes the game would compare the number of players that have passed through each of the six medium rooms and determine which one had the least traffic. The room with the least activity would then spawn a trigger.

When pressed by a player, this trigger would vent every other player into space, killing them and scoring multiple kills for the instigator. (Figure 38 is a view from above the map, and the last thing a player would see before dying.) This encourages "heat" where there is least, therefore creating a dynamic balancing system through mechanics rather than the static graphing. When presented with this scenario, players are given a choice to exercise Steiner point solutions to resolve the spatial problem -- what is the shortest route to the target.

Figure 38

Once the script had identified the room with the least traffic, all players in the map receive both an auditory and a console announcement letting them know which medium room the trigger is available in. Depending on the player's current location, they are presented with two main choices. They can use the risky, but shortest path through the center OR they can navigate the longer, but safer path through the medium rooms, avoiding the central conflict area.

By doing so, we have created two different strategies for players; they can use the middle room as a Steiner node or use the outer rooms as a spanning tree solution (Figure 39). These strategic options play to a player's sense of accomplishment. The player feels a sense of pride, as they feel they are outwitting the rest by taking a shortcut to the proper room. Level assets used to populate the various rooms also served to reduce the total amount of possible Steiner points, creating higher intrinsic value for finding one of the limited solutions.

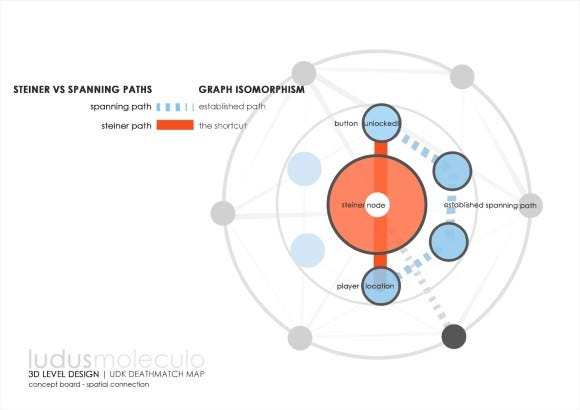
Figure 39

The final published map went through eight major revisions, resulting in updates to either the grey box or the molecules themselves to achieve the final product. Underpinning each revision was a revised molecule concept that would then be converted into a grey box. As such, each revision had clear objectives and goals and the final product benefited greatly from this, as time was extremely limited.

Conclusion

People like Dan Cook and Chris Crawford look at how people's motivation to play games stems from our need to learn and prove these new gained skills. Raph Koster takes this notion further by being even more specific; people are pattern-finding machines and we take pleasure from games when we identify patterns and pre-empt them. It therefore stands to reason that using the pattern-based approach of molecule design to define play spaces immediately plays to this desire.

There is one main consideration to keep in mind; the player doesn't perceive the game as a planar map; they sense it from their own camera frustum. As such, the scale and "identifiability" of the molecules you want to implement is very much limited by how much of the game world the player can perceive at any one point in the game.

Too often designers create labyrinth type maps, which -- although being easily understand from a planar perspective -- are absolutely impossible to traverse when viewed through the limited perspective of the player. As such, molecules and the patterns that they create need not necessarily be complex in order for them to be "fun" for the player.

Instead, well designed game spaces tend to have a number of nested molecules, rather than a molecule that defines the space as a whole. The practical example created by Nassib Azar is relatively simple from a graphing perspective, however the amount of molecule permutations created by the dynamic game elements create a diverse, yet manageable set of strategies for the players to explore.

It is important to point out the use of graphing theory to conceptualize and analyze game spaces is not a new idea, but rather one that has been discussed in various forms by different authors. The original inspiration for this research came from Raph Koster and his Games are Math presentation, and I would recommend Koster's work to anyone interested in rational approaches to design. Joris Dormans also has a few informative articles that deal with how graphing theory can be a powerful tool for level designers. Dormans' Adventures in Level Design and Level Design as Model Transformation [pdf links] are excellent and display the malleability of this toolset.