Trending
Opinion: How will Project 2025 impact game developers?
The Heritage Foundation's manifesto for the possible next administration could do great harm to many, including large portions of the game development community.
Age Of Empires DS designer Tyler Sigman returns to Gamasutra with an entertaining article in his 'probability for game designers' series, discussing how dice-based board game probability teaches us key lessons about design.

[Age Of Empires DS designer Tyler Sigman returns to Gamasutra with an entertaining article in his 'probability for game designers' series, discussing how dice-based board game probability teaches us key lessons about design.]
Be warned: this feature is long and contains a lot of things that are suspiciously and unsettlingly math-like. Go check up on BRITNEY SPEARS or PARIS HILTON or AMY WINEHOUSE if you have a shorter attention span. (Take that, Search Engines!)
I'm currently shopping around a board game prototype called Longship: Viking Raiders. That's certainly not Gamasutra feature-worthy by any means. However, I am long overdue with writing more entries in the critically-acclaimed* Probability for Game Designers series.
- Statistically Speaking, It's Probably a Good Game, Part 1: Probability for Game Designers
- Statistically Speaking, It's Probably a Good Game, Part 2: Statistics for Game Designers
*this is pure speculation on my part
So it occurred to me that Longship had some good examples of applied probability theory in game design. So I've decided to share the design process I used for some of the game mechanics, in hopes that it will be passably interesting -- or at least a temporary diversion from whatever milestone you're crunching towards.

Longship: Viking Raiders Prototype #3 (Board Art by Jeff Simpson)
Longship is a game set at the dawn of Viking raids on the British Isles (circa 800 AD). Each player takes the part of a Viking chieftain bent on plundering the most valuable assortment of treasure possible. Players earn Victory Points (VP) by amassing majorities and sets in any of the six different treasure types (coins, relics, metals, furs, goods, lumber) and also by completing Title Cards, which are individual goals -- think "Achievements", such as "Be the first to sail through every sea zone in one move." Longship is a game for 3-5 players and takes 90 minutes.
By this point, you might be wondering why a board game design article has wormed its way into a site dedicated to the art and science of digital games. Well, hopefully you see a common word in that sentence that answers your own question. I just look at paper as another platform that sometimes has far better graphics and AI than electronic ones... and sometimes far worse. Many bits of design knowledge obviously transfer across the mediums.
The most unique parts of the Longship game design are the dynamic weather system mechanics and the CargoMaster mechanics. By freak happenstance, these also happen to be the most enjoyable parts (according to playtester reviews, not just my random opining). But this Gamasutra feature isn't about either of those. Why? Because, that's why.
Instead, this feature is about the dice-based mechanics in Longship, which make up a small but important part of the game. See, I recently retooled Longship to use custom dice instead of straight d6s, so I thought I'd explain some of the design decisions and math behind the new mechanics that are associated with the dice. Like I stated up front, I really want to show some applied probability theory to prove that it is useful in more situations than just bombastic talks at the Cigars and Brandy Club for Designers.
In some past versions of Longship, it used many more dice, but currently the game uses only two six-sided dice. Crude or sloppy dice mechanics are a hallmark of AMERITRASH design, so once the rest of the game was working fairly well, I decided to take another pass on the dice-related mechanics and give them more polish and personality.
Although I toyed with the idea of removing dice altogether, they have an important role to play in the game. First of all, randomization to some degree can be a very good thing. Some games are superb without it (Chess, Go) but games for a family setting and range of skill levels benefit from some chance. We've seen this in the American classics Monopoly and Risk, but randomness plays an important role in Eurostyle games as well (which I love). Settlers has the all-important (and sometimes detested) 2d6, Carcassonne has the random tile-flipping, Ticket to Ride has card draws and route draws, and so on.

The Game of Goose
The degree of randomness is often what throws games firmly into one design camp or another (Ameritrash or Eurostyle). Subject for another article, but long story short is that too much randomness destroys the meaning of choice in the game, and that's a bad, bad thing for most designers and players alike. While the "GRAND GAME OF GOOSE" was interesting in its day, games like that are just not up to snuff two centuries later. Chutes and Ladders does have its places, I suppose.

2d6 (or two six-sided dice) based mechanics are familiar, flexible, tunable, and all sorts of super things. They are great game tools.

The World Famous 2d6
Familiar: people are used to rolling two six-side dice and don't find it strange at all. Thank Monopoly. Other polyhedrons have an RPG-inspired stigma.
Flexible and Tunable: with 2d6, you can achieve a lot of different number distributions and mechanics. You can use each dice individually, combine them together to get numbers (e.g. Craps), or use one die as tens and the other as ones. If combining them, which is of course quite common, then the probability spread of the numbers 2 though 12 gives you a lot of flexibility to work with. There are 36 different combinations of the dice, so you can make events as rare as 1/36 (2.8%) or as common as you want (by allowing spreads of numbers... e.g. "You succeed on a 3 or above on two dice (97.2%)."
For Longship, though, I wanted something a little more special. Design-wise, there are times when other dice (d4, d8, d10, whatever) are needed to achieve whatever probability or mechanic you are aiming for. When choosing other dice, though, you run the risk of alienating players and/or attaching a strong stigma to the game. Sometimes anything other than a d6 screams D&D to people, which can be bad. Poor polyhedrons, always getting a bad rap.
Before you scream "Stop talking about dice, I'm a digital designer, curse you!", remember that you face a similar crisis of familiarity when coding events related to a random number generator. Sure, you can use percentage-based systems or get as complex as you want in the code, but where user interface is involved, you must still consider familiarity issues. I personally love percentage based systems, but we still see tons of video games with d6ish, d8ish, or d20ish mechanics, and that's partially why.
Returning to our heroic yarn, I wanted a good randomizer with the flexibility of 2d6 but I didn't want to go with a tile deck or card draw or a spinner or some other mechanism that basically screams "I'm dice but I look so much more sophisticated, don't I?" In truth, I needed what 2d6 had to offer but wanted to add a little more theme and interest. Enter custom d6s. After a bit of work, I settled on the following:
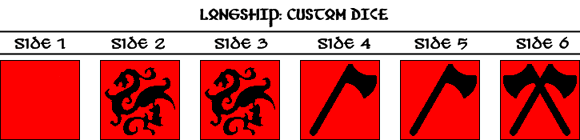
Those two squigglies towards the left are actually sea serpents, by the way.
Why have Axes and Double Axes instead of say, Axes and Swords? User interface issues, honestly. Rather than introduce another symbol, I believe it's more thematic and easier for the player to count number of axes, instead of axes plus swords. It's also easier for me to write tight rules. For example, "You succeed on a 2 or more axes" is easily understood and processed, whereas "You succeed on any of the following combos: 2 axes, any number of swords, or any combination of axes and swords" is not as simple.
I arrived at the above face distribution by process of design iteration. Iteration -- you know, trying something and seeing if it works.
Yeah, I hadn't heard of iteration either until I worked on some paper games.
SFX: RIM SHOT
The writer smiles and briefly envisions a successful stand-up career.
MONTAGE: STAND UP COMIC LIFE, ULTIMATELY ENDING IN HUMILIATION.
But I digress.
In this case, the design iteration for arriving at a good face distribution was mainly just math. That is, I did all the calculations below for some different face distributions and then adjusted the faces and the game rules until I liked the results.
Let's take a look at the numbers and mechanics associated with these new fancy custom dice. Probability, per die:
pBlank = 1/6 = 16.7%
pMonster = 2/6 = 33.3%
pAxe = 2/6 = 33.3%
pDAxe = 1/6 = 16.7%
Armed with this info, let's finally dive into some of the dice-related mechanics in the game. Obviously you don't have a full copy of the rulebook, but I'll try to cover enough detail to give you some context for the rules.
SEA MONSTER CHECK:
Roll both dice. If any MONSTER symbols are shown, then the ship has encountered one.
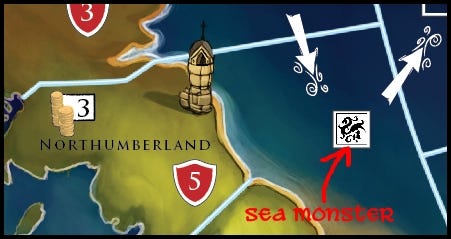
A Sea Monster in a Sea Zone
Any time a Longship sails through a sea zone with a MONSTER in it, any players without Shamans onboard their ship must make a check to see if a vile sea beast is encountered. Hitting a monster results in loss of a crewman and the player must draw a damage card and apply the damage markers to the ship. I wanted this to happen approximately half of the time. (It's always good to have a design goal before you get mired in the numerical analysis.)
To figure the chance of this happening, it's easiest to use the concept of "converse probability." Essentially, we just have to calculate the chance of a monster not occurring on either die, and then subtract this from unity (100%) to see how likely it is for at least one monster to show.
pNOMONSTERS = 4/6 * 4/6 = 16/36 = 4/9.
In plain language, there is a 4/6 chance on each die that a monster will not appear. In order to roll both dice and have no monsters, each die must satisfy this requirement. In this case, we multiply the probabilities as shown above. There is a 4/9 chance of rolling no monsters at all.
pAtLeastOneMonster = 1 - 4/9 = 5/9 = 55.6%
So there is a 55.6% chance of the player hitting a monster. This number is close enough to my design intent for the monsters and shouldn't really require any major balance tweaks.
Since there is a 2/6 chance of rolling a monster on each individual die, it's very easy to make the mistake of trying to calculate the chance of rolling at least one monster on two dice this way:
pAtLeastOneMonster(WRONG) = 2/6 + 2/6 = 4/6 = 2/3 = 66.7%
To see why this is erroneous, consider rolling 2d6. What are the chances of rolling a 4 or above on at least one die?
p4orAbove(WRONG) = 3/6 + 3/6 = 6/6 = 100%.
Hmmm, suspicious. Rolling 2 dice, you certainly are not guaranteed to roll 4 or above on at least one die, yet this calculation says you should be. As a general rule of thumb, if you are doing probability calcs that say an event is 100% likely to happen, most of the time something has gone wrong.
It gets even worse if you look at the chance of rolling 2+ on at least one die:
p2orAbove(WRONG) = 5/6 + 5/6 = 10/6 = 167%.
Danger, Will Robinson! You've invented the equivalent of the perpetual motion machine! (http://en.wikipedia.org/wiki/Perpetual_motion_machine). It's just not valid to add probabilities when you have two independent events going on. Here, each die is an independent event.
You can only add probabilities when you have a single event with multiple success criteria -- for example, checking for a King or an Ace by drawing one card from a deck. In this case,:
pACEorKING = 4/52 + 4/52 = 8/52
This is a totally valid way of adding probabilities, because you are just adding success criteria for a single event.
The proper calculation when using two or more independent events is more complicated. But using converse probability makes things a little easier, as demonstrated in the monster calculation above. Just ask yourself "how likely is this NOT to happen" and then work backwards.
See if you can redo the p4orAbove and p2orAbove calculations above using conditional probability. You should get 75% and 97.2%, respectively. Note: for another stab at describing conditional probability, see "Probability for Game Designers".
Raiding a Land Territory
Roll both dice when attempting a RAID. If you raid a territory that has equal or lower strength then your longship, then you must roll at least 1 axe to succeed. If the territory is higher strength then your longship, then you need at least 2 axes; also, no monsters may be showing.
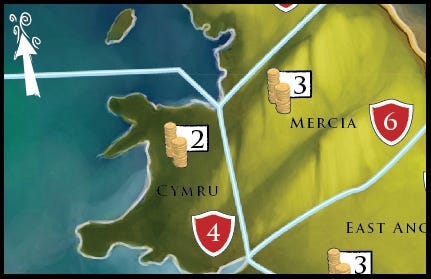
Cymru (Wales) Has a Strength of 4, Mercia has a Strength of 6
Chance of rolling an Axe, per die:
pAxe = 2/6 = 33.3%
Chance of rolling a Double Axe, per die:
pDAxe = 1/6 = 16.7%
Chance of rolling at least one axes' worth, per die:
pAxeOrBetter = 3/6 = 50.0%
pNoAxe = 6/6 -- 3/6 = 3/6 = 50.0%
Chance of rolling at least 1 total axe on two dice (use converse probability):
pNOAXES2DICE = 3/6 * 3/6 = 9/36 = 25%
p1AXEorMORE = 1 - 25% = 75% < -- Raid success when equal or stronger
Now to the other raid situation (raiding when weaker than the land territory). The chance of rolling at least two Axes on two dice AND no monsters are showing can be calculated different ways:
Method 1 (adding individual probabilities):
pAnswer = chance(exactly 2 axes with no monsters) + chance(exactly 3 axes with no monsters) + chance(exactly 4 axes with no monsters).
The first component is the chance of "exactly 2 axes with no monsters."
p2AxesNoMonsters = 2/6 * 2/6 + 1/6 * 1/6 + 1/6 * 1/6 = 16.7%
The only combos that satisfy this are when both dice show one Axe, or either die shows a Double Axe but the other die doesn't show Monsters or Axes. So the 2/6*2/6 component is the chance of both dice showing an Axe at the same time; the 1/6*1/6 component is when one die shows a Double Axe and the other die shows the only valid result: a blank (anything else is an axe or a monster, which doesn't count towards p2AxesNoMonsters). This 1/6*1/6 is counted twice because you can have the combo two ways: Double Axe on die 1 and Blank on die 2, or vice-versa.
The other chances are figured similarly:
p3AxesNoMonsters = 2/6 * 1/6 + 1/6 * 2/6 = 11.1%
p4Axes = 1/6 * 1/6 = 2.8%
pAnswer = sum of the above = 30.6%
If none of this method made sense, you're in luck. Brute Force can often overcome what fancy figuring can't.
Method 2 (Brute Force):
Count the actual dice combos and figure probability by doing ratios.
pAnswer = [(number of combos for rolling 2+ axes) - (number of combos of those that has a monster) ]/(number of total combos).
To figure this out, let's go ahead and list all the combos:
Longship Custom Dice Combo Enumeration
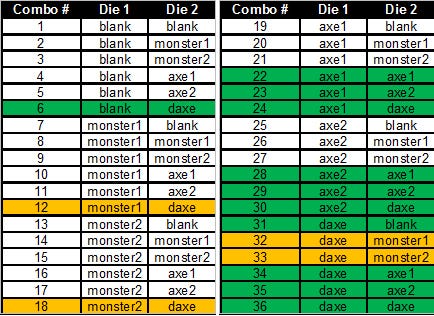
Number of total combos on 2 dice = 36
Number of combos with 2+ Axes = 15 (shaded green or orange)
Number of those that has a Monster = 4 (shaded orange)
pAnswer = (15 - 4) / 36 = 11 / 36 = 30.6%
Casualties while Raiding:
Lose one crew member for every monster rolled during the raid attempt.

Blaaargh! (image courtesy Chris Bourassa)
When Raiding a land territory, you can always lose some crew, regardless of whether you win or lose in the Raid. Every monster you roll results in a crew loss.
We already derived the chance of rolling at least one Monster on two dice earlier. Repeated here for convenience:
pAtLeastOneMonster = 1 - 4/9 = 5/9 = 55.6%
But wait, that's only part of the story. So far all we know is that the player will lose at least one crew member a little over half the time. However, there's another layer to the mechanic. The rule states that the player loses one crew for each monster showing. So although we know the player will lose some crew 55.6% of the time, as thorough game designers we should really calculate the average number of crew lost. Put simply, we must account for the fact that sometimes the player will lose two crew at the same time (by rolling two monsters).
To calculate the average crew lost, we need to do an "Expected Value", or EV calculation. This will be familiar to anyone who studies Game Theory, or perhaps anyone who reads a lot of poker books! (Sadly, I fall into both categories.)
EV is essentially the chance of something happening multiplied by the value of that result. When you're talking about poker, you are multiplying the chance of a hand showing up by the money you'll win if it does, but you are also including the chance of the hand not showing up multiplied by the amount of money you lose. If the EV is positive, it's a worthwhile value bet; if it's negative, then math says you'll lose money in the long run. Sure, you might get lucky here and there, but if you make the bet 1,000,000,000,000 times, you will come out behind.
For Longship, I just want to know the EV in relation to how many crew will be lost. Maybe after I do the calc it will make more sense, because all this writing is confusing me, too:
EV = ChanceOfEvent1 * value1 + ChanceOfEvent2 * value2 + ChanceOfEvent3 * value 3 + etc.
Also seen as: SIGMAAAAAAAAAAAAAAAA
EVaveragecrewloss = (pExactly1Monster * -1 crew) + (p2Monsters * -2 crew)
pExactly2Monsters = 2/6 * 2/6 = .111 = 11.1%
pExactly1Monster = .555 - .111 = .444 = 44.4% (we know we will hit at least one Monster 55.55% of the time and we know p2Monsters = 11.1%, so p1Monster is what's left.)
EVaveragecrewloss = (.444 * -1.0) + (.111 * -2.0) = -0.667
Therefore, on average the player will lose 2/3 (66.7%) of a crew member whenever they raid. This is significantly different than the 55.6% chance of losing at least 1 crew. It should be accounted for during game balancing.
This example illustrates one of the easiest probability mistakes made when assessing 2d6 combinations and results. On one hand, you can calculate the chances of, say, at least one "6" showing up on two dice (a). But if each individual "6" actually counts for something, then you really need to make sure that you account for it (b). If all you are looking for is "at least one six", then it doesn't matter (similar to the sea monster check earlier in this article).
To drive the point home and use another game example, let's say we have a pirate game (because we all should) and in the game, cannons hit long distance targets on a "6″. You have two cannons on your ship, so you roll two dice when firing.
pChanceOfHittingAtLeastOnceWithTwoCannons = 1 - (5/6 * 5/6) = 36/36 - 25/36 = 11/36 = 30.6%.
In other words, there are 11 out of 36 combos for which at least one hit ("6″) occurs. You could have arrived at this number by brute force by counting of the combos instead of the converse prob calc. But converse probability was a bit faster.
Now let's calculate the "EV" of two cannons at long range, since this is what we'll use for game balancing. To do this, we need to know how those 11 special combos break down. As it turns out, 10 of the combos are hits with 1 cannon, and only one combo is a hit with both cannon. See, there are 10 ways to roll 2d6 and get a "6" on only one die, but there is one way to roll 2d6 and get a "6" on both dice.
Average Number of Hits Scored = EVcannonhit = (comboswith1hit / 36 * 1 hit) + (comboswith2hits/36 * 2 hits) = [(5+5)/36*1] + [1/36 * 2] = 10/36 + 2/36 = 12/36 = .333 hits
You'll hit 30.6% (.306) of the time on average, but the average number of hits you will cause is .333. Sometimes ya hit 'em with both barrels!
Boom-chikka-Boom: 1/36th of the time!
If this is still confusing, then I guess I succeeded at least in illustrating the deceptively easy mistake you can make when looking at 2d6 combos. Most of the time, it's not a huge deal. But make a couple percent error when building a satellite, and it will pancake on Mars instead of nicely landing. Bye bye billions.
The game, that is. Another rule:
Razing Territories:
Roll 1 die. The territory is razed if any axes show.
After taking the last treasure from a territory, there is a chance that it gets razed. This means that the place is temporarily exhausted of all valuable relics, coins, peasants, and so on. Razed territories take longer for the territory to refill with treasures. This makes some territories suddenly less valuable for a while, which creates some dynamic game situations.
I decided I wanted a simple 50/50 chance here. Design-wise, I didn't want it to raze all the time (playtested that, didn't like it) and I also didn't want things not to raze because I like the dynamic aspect.
Getting 50/50 was fortunately the easiest calculation yet. For this rule I went with a simple one die resolution to speed things up and also to differentiate the roll from the raid check immediately preceding it. If any axes show at all, the territory is razed:
pRaze = any axes at all on 1 die = 2/6 (single axes) + 1/6 (double axe) = 3/6 = 50%
As is tradition in my articles, if you've made it this far then you should either be commended or committed. Hopefully, this feature has helped illustrate some of the design process that goes into something as simple as a dice roll.
If you enjoyed this article (or didn't!), please be sure to let myself or the awesome Gamasutra editors know. It may affect how often they let me out of the box in the future.
Also, if Longship sounds interesting and you want to know about a potential commercial release, please drop me an email.
Read more about:
FeaturesYou May Also Like