How random is that?

Disclaimer: in this article, as with all my articles, I claim to hold no universal truths, or even remotely accurate information, all opinions are based on personal observation and speculation. Criticism is all around welcome, as long as arguments are provided. Thank you.

Ok, let me first clarify that this article is not intended for players, as the title and description might suggest. I will go over the cause of the mentioned phrase form a developer’s standpoint. And no, it (usually) has nothing to do with the randomization in the system being biased or bugged. Of course there are cases, when a bias is intentional; I will go over these instances separately.

The scope of this article is also not limited to just the perception of random systems by players; I’ll go over systems with random values as a whole, how they might be perceived, average values, several common pitfalls designers encounter while working with random values in their systems, thoughts on die versus flat number ranges and why the two should never have а “=” between them.

I’ll first start by stating, that if you want to become a competent systems designer, you’d do well to pick up on some math skills (among other things, which are not the subject of this rant, however), especially probability theory and statistics; don’t let this discourage you, though as the basics should be enough for most tasks. A good(ish) read to start off with would be this book: http://www.amazon.com/Mathematics-Game-Developers-Development/dp/159200038X, but be aware, that it focuses primarily on programming, instead of actual game design (which is not, in itself, a huge problem, as the more a designer knows about programming, the better). A surprisingly good direction to look at is the math course required for a typical major in economics.

Random Number God?

Anyhow, random numbers. What are they and what do we need them for in a game? Well, the simplest answer I can come up with is: they add a certain degree of unpredictability to a system, and, therefore, the game that utilizes that system. If done right, implementing something, running on random numbers might add variety, diversity, longevity, strategic depth, replayability and all sorts of other cool things to the experience.  “Hold on, would a game without any randomness to it be any good?” you might ask? Well, yes, take chess for example. The strategic depth of that game is, arguably, unmatched by anything else to this very day, however chess had hundreds of years to mature and has an opposing player providing the oh so needed unpredictability. A second question might follow: “You make it sound like being predictable is bad for a game. Why?”. Weeell, to be entirely honest, I don’t know. I doubt anybody really knows, and I’d be the first in line to start throwing stones at someone who claimed that they did. It’s just one of those complex human psych things, that are better left to the PhDs. It’s not to say, that predictable outcomes and routines are a bad thing, on the contrary, the opposite is actually fairly annoying in a game. So, let’s just take it on faith that a game, in which every single action produces a 100% predictable result, is not going to grab a player’s attention for very long.

So, how do we go from random numbers to actual ingame content? Well, the simplest way to do that is by implementing an RNG (random number generator) routine into your game mechanics. This can work in a myriad of ways, based on the type of game, the particular system that you are using it for, the RNG routine itself, and a host of other conditions. But the general principle is always the same. You take something that generates a random number, and then use that number to define the outcome of a random event.

Random event – this is an event that the observer has no way of predicting the result of 100% of the time. Basically if you have event A, which produces result X every single time, that’s not a random event. If you have event A, which produces results X and Y and you can’t predict, based on conditions (this is important), which one it’ll be, that would make it a random event. I also have to mention that a random event stops being one once the observer acquires the means to reliably (100% of the time) predict the outcome. Saying that the result will be either X or Y with 50/50 chance is not a “reliable prediction”, it’s cheating (well, actually, it’s called probability and is also very important to calculate, but we’ll get to that later).

Let me give you an example of a system, which produces random events based on a number, generated by an RNG routine.

Let’s say that a certain Mob drops loot when it’s killed. The loot may contain one of the following: sword (S), helmet (H) or potion (P). If we split this into [events] and {results}, we’ll get the following:

[Mob gets killed] -> {Mob is dead} -> [Loot is calculated] -> {S, H or P is dropped}

Now, event [Mob gets killed] is not random, because, in this case, the result of a mob getting killed is always the same – a dead mob. However the event [Loot is calculated] is a random event that may produce one of the mentioned results. How is this done? Usually a predetermined weight is assigned to each of the probable results (sometimes percentages are used, but I’ve seen weights being used more often), which adds up to a certain range of values. For simplicity’s sake, let’s say all items should drop with the same chance. That would give a weight of 1 to each item and an integer range from 1 to 3. Then, during runtime (a fancy way of calling a launched game), the loot calculation event calls a value from the RNG, interprets that into an integer and uses it to determine which item from the list should drop as loot. If the RNG works in a range from 1 to 1000, then the loot drop event would interpret 1 – 333 as a 1, 334 – 666 as a 2 and 667 – 1000 as a 3.

It’s usually fairly more complex than that, because there’s always some form of interpretation running between the RNG and the various systems that use it, or there might be several different RNG routines running for the different events and mechanics that need randomizing, but, in general, that’s the idea.

Different Flavors of Random

The following is a personal classification of said events as pertaining to systems design, based on how the random event is created.

Natural – is randomized based on events or player actions, uses no RNG routine.

An example of this would be a deck of cards, that always starts out in the same order, but from which a card is drawn by an undetermined amount of players, before you get to it.

The pros of natural randomization are that, if done right, it can lead to a very strong sense of emergent gameplay and player involvement.

Cons – very difficult to get right and always has an associated danger, that players will discover the pattern for reliably predicting the outcome of events, where it’s detrimental to gameplay.

Artificial – uses an RNG routine to get randomized.

An example would be a deck of cards, which is shuffled by a machine every time a player draws a card from it.

Pros – it’s a tried and true way to add variety and unpredictability to gameplay.

Cons – often encourages a feeling of disconnect between player action and outcome, especially when incorrectly used in macro gameplay systems, e.g. determining hit/miss chances for combat mechanics in, say, an FPS game (this is an extreme example, but I’ve personally seen it done and it gets the point across).

For all intents and purposes, I consider this classification of different randomization principles more than adequate for the purposes of identifying how to randomize events for a player on a global scale in a given system. The rest is merely figuring out the specific details for each event (event type).

Also, I consider applying both principles to the same group of events within a system is redundant and will make it almost impossible to predict outcome probability, which is bad for both gameplay, and gameplay analysis, so don’t do it. However, stacking them onto sequenced events can lead to some interesting, unexpected and, often worthwhile, results.

Random Me This

Ok, that takes care of most of the theory, so let’s get back to the question raised in the beginning of the article.

If you follow any forum of nearly any heavily multiplayer game (be it a persistent universe MMO, MOBA, or stat-based competitive multiplayer game), you’re more than likely to come across a thread, where a number of players will rant about how the “random is totally broken/unfair/abusable etc…” (and if you’re that thread starter, then pay very close attention, because I’m going to tell you why you’re totally wrong), and another type of thread, where users are making up fables about how procs (slang, meaning a random event resulting in a rare outcome) are “moar likely to happen if you turn your monitor upside-down and hold your breath for a FortnightItWorksITested!!!111…”

Both cases are the result of misinterpretation, because people are fairly good at calculating averages, but completely miss the point, when trying to understand what those averages actually mean. Now, this part of the text wouldn’t make the cut into the article, if designers, especially inexperienced ones, didn’t systematically make the EXACT same mistake. The situation is so bad, that it eventually became the central theme.

An average is just that – an average. It’s usually not even a weighted average.

Let’s say we have a sword that does 6 – 10 damage per hit. The average damage for that sword would be 8. And here’s where things get funny for most people – once the average is calculated in the player’s head, he begins expecting the sword to generally do around 8-ish damage on each hit, completely failing to realize, that the average of 8 can be made up of multiple times of 6 and 10. And, as an aside, DPS (damage per second) ratings seem to further exacerbate the issue.

Furthermore, players would always seem surprised to get 6 damage, say, four times in a row. But let’s do a quick and dirty calculation here:

The probability of landing a hit for 6 damage is 20% for the given flat probability range. Hence the probability to land 4 consecutive hits for 6 damage would be 0.2^4=0.0016, which is 0.16%. Doesn’t seem like much, does it? Let me put this into perspective. If we take 1000 hits and calculate the probability to land four consecutive 6 damage hits for that, we would get the following picture:

1-(1-0.0016)^100~0.7983, which is a whopping 79.83% (I’m not going to go into the specifics on why exactly the calculation is done this way, because that would mean giving a primer on probability theory, also the final value is not entirely accurate, as I used a very quick and dirty method that doesn’t take into account proper distribution, but I assure you, the result is within acceptable error limits for the sake of this demonstration). All of this means that when triggering an event 1000 times, which has a 20% chance to produce a result, you are almost guaranteed to proc that result four times in a row at some point. And if this sword lands a hit every second, you’ll be seeing this effect roughly once every twenty minutes, which is not that rare in fact.

Yes, I know, wow, right? It’s as simple as that.

And the second misinterpretation comes from that fact that it’s common for people to associate the extremes of random systems to unrelated events, just because they happen to overlap chronologically, it’s a defensive mechanism, that alleviates frustration, among other things (yes, this is way out there in the “best left to the PhDs” department).

Here be Randoms

All of this leads up to the fact that more often than not, designers tend to make mistakes with their random systems, which lead to no end of frustration for the player (this is mostly evident in MMOs, but also can lead to serious problems in almost any game).

Here’s an example:                                    

An item has a drop rate of 10%. The player needs that item to complete a quest/advance the story/get a top-tier reward etc… doesn’t really matter. It’s just a highly desirable item. Also, this item is not tradeable, or we’re talking about a single player game. In any case, the player can only get it through random drop from killing a certain mob.

A 10% drop rate means that on average, every player is going to acquire that item after 10 kills of that mob. Doesn’t sound too bad, but I’ve already demonstrated that average values alone are an entirely useless metric. Let’s take a look at what happens in the outlying regions of the range.

There, of course, will be those that receive the item on their first try (about 10%). And, on the other end of the scale, we will have a roughly 0.5% chance, that the player will receive nothing after 50! attempts. That’s roughly one player lost to frustration for every two hundred players in your game. If you have 10 events that generate this kind of behavior, it’s a potential loss of one player per each event per two hundred players. All because someone hasn’t been doing their homework =)

This doesn’t necessarily make the described event a bad design decision. A bad design decision would be to implement it in such a way that forces the player into an abnormal gameplay situation. If your average is calculated as 10 kills per item, a kill count of 50 to get that item would be classified as a bad design decision. Here are several possible ways to avoid this:

Conclusion? Pay attention to how and where you use probabilities, always consider outlying cases and how they would impact gameplay, because with enough players, there will be instances of hitting the entire range of probabilities, including the ones that are potentially game breaking. And just generally pay close attention to any numbers, wherever you may be using them. Don’t use a value just because it looks good, there has to be solid reasoning behind using one value over any other.

Role of the Die

I’ve seen a lot of designers disregard die rolls in game systems as an anachronism and something far less flexible than flat value ranges. I have a very strongly held opinion that this is not the case. Most arguments against die that I’ve heard are somewhere along the lines of:

And here are my counterarguments:

Following is a visual comparison of what the probabilities would look like, when presented on a graph.

A flat value range 2 – 14 (average is 8):

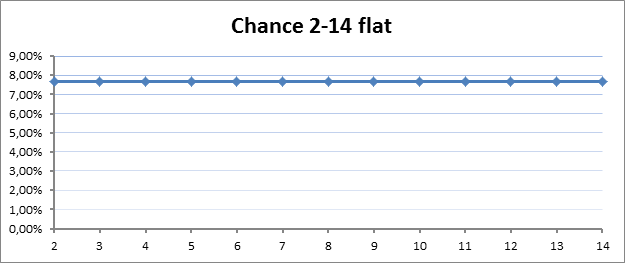
Flat value range

A 2d7 value range (again, average is 8)

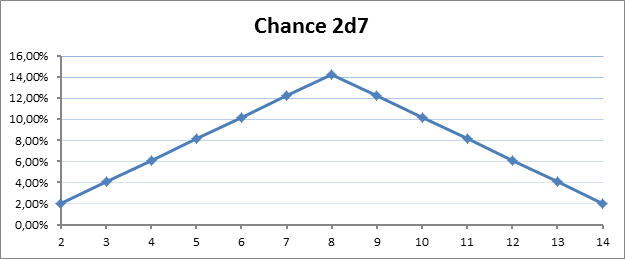
2d7 die roll

A 4d3 value range (and again, average is 8) note: the more die in the roll, the more “curvy” the line will become, and the further the probabilities will shift towards the average value.

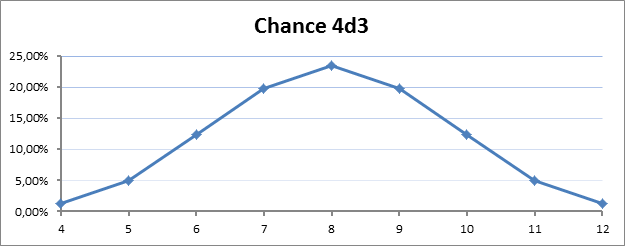
4d3 die roll

As you can see, all the different setups have the same average value to them, and that’s exactly why there is a common misconception about there being no difference in the probability, most people just don’t bother to look any further.

Let me give an example of the impact this might have on the actual gameplay.

Let’s say we’ve got two weapons. One uses a flat damage range 2 – 12, the other uses a 2d6 die roll; and we have a mob that has a damage threshold of 10, which means that any damage below 11 will not go through the mob’s defenses. In this case the better weapon would be the one with the flat value range, as it will proc the 11 and 12 damage with a probability each 7.69%.

Say we’ve got the same weapons, but now, every time the mob is hit with terminal damage values (6 or 12) it stacks a small stat boost on itself. In this case the preferred choice of weapon would be the 2d6 one, as its variance distribution is denser the closer it gets to the expected value, than at the terminal values.

Probably later

So, final thoughts. The 2 primary methods described in this article, i.e. flat value range and die rolls are not the only ways to handle a random event within a system. For instance, you might want to weigh your values based not just on mathematical distribution, but on other artificial conditions. But they are the ones used most often; in all other circumstances the issues are resolved on a case-by-case basis. Unless you’re going for something different on a conceptual level, then you’d specify the system and your approach to it in the design.

Also be on the lookout for potential errors in your reasoning when working with randomization. Always remember that there are extreme cases associated with random values, unless there is a specific mechanism in place to mitigate those extremes.

Again, the goal of this article wasn’t to tie the whole random thing into the psyche of game design, that’s a topic for a whole series of articles, or even a book, I was attempting to show on a practical level what random is, what it’s for, how to use it and what to avoid on a very elementary level with simple examples. Here’s hoping some of you will find this useful.