Trending
Opinion: How will Project 2025 impact game developers?
The Heritage Foundation's manifesto for the possible next administration could do great harm to many, including large portions of the game development community.
Game design veteran Sigman presents a detailed look at how game mechanics can be represented visually -- and what we can learn about how to make great video games thanks to such alluring graphs.

[Game design veteran Sigman presents a detailed look at how game mechanics can be represented visually -- and what we can learn about how to make great video games thanks to such alluring graphs.]
Whether discussing game features amongst the design team or communicating them to programmers, lack of proper terminology can obfuscate messages. (Just like how using the word "obfuscate" can obfuscate messages.)
Coders have technical backgrounds and most went through rigorous college-level math classes. As a result, if a designer is trying to explain a desired mechanic but using the wrong terms, the message content can be lost.
The foundations of math provide a convenient basis for understanding most game mechanics, so it generally makes sense to describe game mechanics in established mathematical nomenclature.
The first part of this article is a short primer on visual representation of game mechanics and some proper terms to describe those representations. The second half discusses a few selected game mechanics in more detail for illustrative purposes.
A picture's worth a thousand words.
No, seriously. I was trying to think of a wittier, more concise way to explain the value of talking about game mechanics visually, but societal wisdom beat me there.
The hitch about using visuals is that you still need a way to describe them. So you kinda still need those thousand words after all. So let's dive in with some foundation items, and then we'll get to the fun stuff.
Term: Function
Mathematically, a game mechanic is usually just a function. A function is a mathematical "black box". Given a certain input, the black box (game mechanic) creates an output.
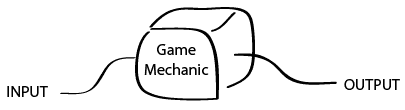
Game Mechanics are Functions (Black Boxes)
Graphically, a function is represented by a line or curve in an X-Y plot:
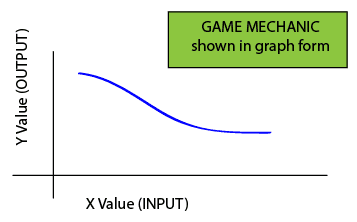
A Function
Term: Domain
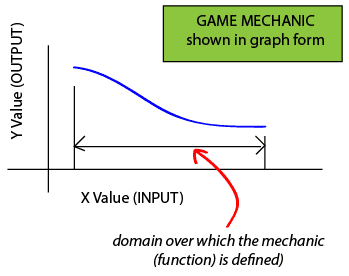
Function Domain
A game mechanic's domain is the range of values over which the mechanic is active. Graphically, this is represented by the X-axis ("abscissa").
Take an example game mechanic: "shooting accuracy as a function of RIFLE skill." The domain is the RIFLE skill range -- say 1-10 or 1-100 or whatever your game system is.
Another example is the mechanic "acceleration as a function of transmission gear." In this case, the domain is the range of gears in the vehicle -- say 1 through 5.
Term: Slope
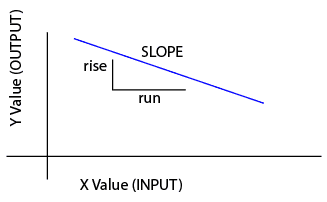
Slope
Slope refers to the angle of the line or curve of a graphed mechanic. Technically, slope is described as "rise over run", which is just the change in Y value for a given change in X value. Negative slope means downward trending; positive slope is upward trending.
Conceptually, a high slope means a fast-changing mechanic, whereas a low slope is a slowly-changing mechanic.
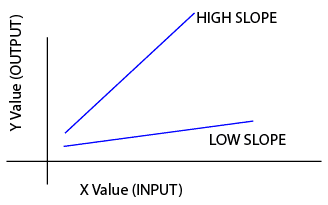
High and Low Slope
Whether the mechanic is linear or non-linear (see later), you can always still define a local slope. In the case of a linear mechanic, the slope is constant; for non-linear mechanics, the slope changes all over the place.
One of the most useful descriptive characteristics of a game mechanic (a.k.a. function) is whether it is linear or non-linear. Linear is pretty much like it sounds -- "like a line". Mathematically, this means the slope of the mechanic is constant. Practically, this means that the mechanic steadily increases or steadily decreases at a given rate.

Linear Mechanics/Functions
Examples of Linear Mechanics:
Simple steering: position of the steering wheel corresponds linearly to turn rate
Simple weapon damage as a function of charge-up time: if you charge up for 2.0 seconds, the damage is twice what it is if you charged up for 1.0 seconds
Simple To-Hit Chance as a function of weapon skill: having a Weapon Skill of 50 gives the player two times the chance to hit as a Weapon Skill of 25.
Simple XP Rewards as a Function of Monster Level: defeating a level 4 monster gives twice as much experience as defeating a level 2 monster
Term: Non-Linear
If a mechanic is not linear, then it is non-linear. I know -- big surprise.
For every linear mechanic out there, there's probably a non-linear one. Well, maybe not that many, but the point is that non-linear mechanics are extremely common. Sometimes you need to use a non-linear relationship because a linear mechanic just doesn't accurately simulate or accomplish your design intent.
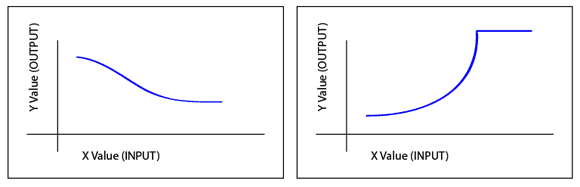
Non-Linear Mechanics/Functions
Examples of Non-Linear Game Mechanics:
Almost every RPG character level advancement XP table ever created (you can thank the late Gary Gygax or Dave Arneson for that): it might take only 1,000 XP to climb from level 1 to 2, but it could take 1,000,000 XP to climb from level 20 to 21.
Population growth in Civilization: your Year 500 Civ will typically have more than five times the population of your Year 100 Civ... unless you're on your way to extinction.
Car acceleration as a function of "seconds from the line" in a driving game: real cars have higher acceleration in lower gears and lower acceleration in higher gears. You may travel 0-60 in 6 seconds but you can't expect to gain another 60 MPH in the next 6 seconds.
Score as a function of time played in Geometry Wars: if you can last 20 minutes, you'll surely have far more than twice the score of someone who played for 10 minutes.
Non-linear mechanics are very familiar to us and more colloquial ways of describing them exist. For example:
"the law of diminishing returns"
"geometric expansion"
Types of Non-Linear Mechanics
While linear mechanics differ only by their slopes, there are many different types of non-linear mechanics. It is often necessary to subclassify them further as one of the following:
Asymptotic to a value: these mechanics tend to "flatten out" as they approach a certain result (y value). After a point, huge changes in X result in very small (insignificant) changes in Y. In other words, slope approaches zero after a certain point.
Example Mechanic: to hit chance based upon weapon skill: you might design a combat system that eventually "tops out" the player's chance to hit as his weapon skill increases. After a point, further increases in weapon skill have little effect.
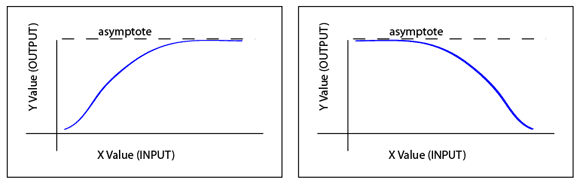
Asymptotic to a Value
Asymptotic to infinity: these mechanics tend to approach infinity (Y) as X increase or decreases.
Example: Population Growth (geometric expansion). Technically, some limit will eventually exert itself (e.g. capacity of the planet?), but until that limit, the mechanic may follow an Asymptotic to Infinity relationship.

Asymptotic to Infinity
Non-asymptotic: the non-linear mechanic doesn't ever "level off" and isn't asymptotic to infinity.
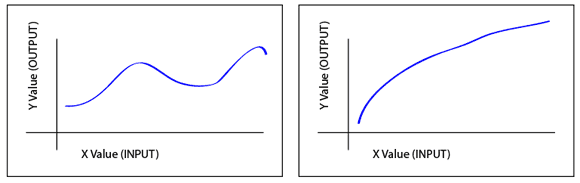
Non-Asymptotic
Segmented Linear
A segmented linear mechanic is technically non-linear overall, but you can think of it more as just a linear mechanic that is made up of two or more sections with different slopes.
An example of a segmented linear mechanic would be a really simple car transmission mechanic where you are modeling acceleration and torque as a function of speed. Each gear would have different values. The resulting graph would be made up of several different linear "gear bands", each with a different slope.
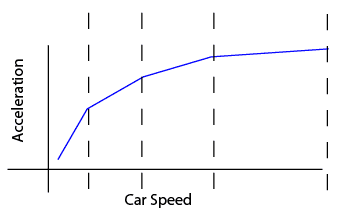
Segmented Linear Mechanic: Notice the Distinct Linear Sections
Segmented Linear mechanics are relatively easy to create and often are a great way of simulating a complex non-linear mechanic. If the assumption that the mechanic is linear between various key points is good enough, then it can be a good way to go and they are very tunable.
Linear and Non-Linear Living Together
If you like chocolate and you like vanilla, why not combine them together and have both? In and Out Burger doesn't fight you on that, so you shouldn't fight yourself. When designing a game mechanic, there's no reason why you can't have some portions of the domain be linear and some non-linear.
However, you should probably avoid such complexity unless you have a really good reason. (See next page.)
Designing game mechanics is part science, part artistry. Typically you have to make trade-offs between simplicity and accuracy. All sorts of factors should be weighed in a design decision: How accurate of a simulation do you want? How well known is the mechanic you are trying to model? How simple will it be to tune, retune, and balance? Will other team members understand it enough to work on it? Will the end-user (player) understand it? And so on.
Sigman Design Rule 41a: Choose the simplest mechanic that satisfies your design goal.
KISS and all that. This is similar to a very handy axiom in AI Programming. Remember that your goal is not to make the most eloquent/advanced/innovative SYSTEM, but rather to accomplish a DESIGN GOAL with the minimum amount of required work. In other words, your game mechanic only needs to be as clever as it needs to be. A bit Zen-like, but true.
This isn't to say always go simple -- sometimes a design goal can only be achieved with a complex system. But always go as simple as you can get away with, because that will facilitate easier tuning, adjustment, iteration, and understanding.
In order of simplicity of implementation:
Linear mechanic
Non-linear mechanic defined by a single equation (e.g. y = x2)
Segmented Linear mechanic
Non-linear mechanic defined by multiple equations and/or combined linear/non-linear mechanic
However, don't confuse implementation complexity with the complexity that the player sees or experiences!
Sigman Design Rule 41b: Complexity of implementing a mechanic does not always equal the player's complexity of understanding that mechanic.
Non-linear mechanics are usually more complex to implement than linear mechanics, but they aren't typically hard to understand! Like I mentioned earlier, concepts like "diminishing returns" are intuitively familiar to many people. The reason is that we encounter tons of different mechanics in everyday life, and many of them are non-linear.
It is not hard to understand that a car's acceleration varies over its 0-60 run (as gears are changed), or that bunnies multiply exponentially, or that your financial investments can behave any number of ways in between key time periods. People observe mechanics all around them every day, even if they aren't thinking about it.
If you are making a simulation or an arcade action game, studying real-life mechanics is hugely important to game design.
A Few Linear Mechanics in Life
Travel speed and distance: if you travel at 120mph in a straight line, you cover twice as much distance per hour as you do traveling 60mph in a straight line. Yes that sounds obvious, but that's a linear mechanic for you!
Kinetic energy as a function of mass: a flying object moving at 50 feet per second and weighing 2 lbs. has exactly ½ of the kinetic energy of a flying object moving at the same speed but weighing 4 lbs.
Temperature in the troposphere: temperature tends to decrease at a steady rate ("lapse rate") from the surface on up to the tropopause.
A Few Non-Linear Mechanics in Life:
US Federal Taxes: thanks to the myriad of factors involved in US taxes (including tax brackets, phased out deductions, and a million other things), someone who earns 100k isn't guaranteed to pay twice as much taxes as someone who earns 50k. But even within your own tax return, you pay more taxes for the last $10 you earn than the first $10 you earn (assuming you make enough to hit the second marginal tax bracket). The core tax bracket system is segmented linear.
Weight training: for every hour you do strength training, you don't gain the same amount of strength. Sometimes you have rapid gains, and sometimes you plateau for a time. (non-linear decreasing)
Population growth: if you look at human history in 10 year segments, the amount of new people born each decade increases non-linearly. (non-linear increasing)
Compounding Interest: if you invest $1,000 in a 5% earning money-market account at age 20, it will be worth $7,040 at age 60. If you had invested the same $1,000 at age 40, it would only be worth $2653 at age 60 (37.7% of the former). If interest compounding was a linear mechanic, you would have expected a 20 year investment to be worth exactly 50% of a 40 year investment. (non-linear increasing)
Salary as a function of years of experience (Ok, the Game Developer Salary Survey is always on my mind): someone with 15 years of experience doesn't typically make 3 times what a person with 5 years of experience makes. (non-linear decreasing)
Gravity: the attraction of two bodies decreases non-linearly with distance. If you weigh 200 lbs. at Sea Level (~4,000 miles distance from the center of the Earth), you will actually weigh far less than half of that at an altitude of twice that.
Kinetic energy as a function of speed: a five-pound object moving at 50 mph has four times as much kinetic energy when moving at 100 mph (non-linear increasing)
A normal (aka "bell shaped") distribution of data (see my Statistics article <LINK>): values in the upper 10% band are far more rare than those in the middle 10% band.
Ok, enough about real life. Let's do a couple quick case studies of actual game mechanics.
Quick Description: Characters gain "levels", which correspond to predefined improvements in key attributes and skills. It takes a certain amount of Experience Points (earned through completion of various tasks) to gain levels. Later levels cost vastly more Experience Points to advance than early levels.
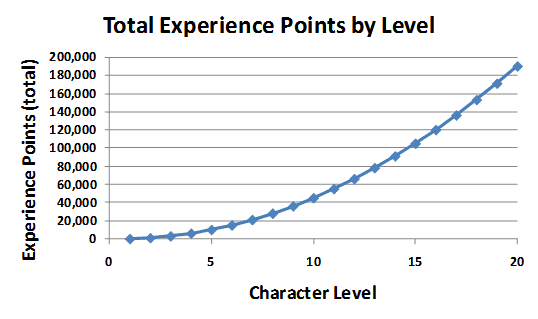
Typical Experience Point / Level Chart
Dissect It!
When it comes to an experience point system, there are two main ways of skinning the cat. Method 1, which is by far the most popular, uses an experience point curve like that shown above -- experience to reach the next level increases non-linearly. Only 1,000 may be required to achieve level 2, but you'll need a total of nearly 200,000 to reach level 20.
This system was used in the grandpappy of all RPGs, Dungeons and Dragons. The advantage of this system is that bigger monsters award the player larger XP numbers, so it is easy to compare monsters on an apples to apples basis. Also, the players feel a sense of accomplishment in gaining the larger rewards.
For completeness' sake, the other common system for XP/Levels involves keeping a constant level ramp (say 1,000 XP per level) but adjusting XP awards for monsters to be relative to the players. For example, defeating a kobold with a level 1 character may yield 50 XP, but defeating the same kobold with a level 10 character might only award 5 XP.
Quick Description: In this game, the player earns 200 gold per turn for each mine. If you have 3 mines, you earn exactly 3 times the income of 1 mine (3 x 200 = 600 gold), not counting tech bonuses.
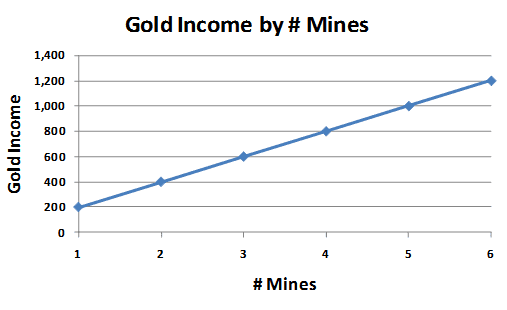
Gold Income as a Function of # Mines in Age of Empires: the Age of Kings DS
Dissect It!
This income mechanic is totally linear. More farms gives a directly-proportional increased food income.
Why do you think the designers chose a linear mechanic in this case?
I have a strong suspicion* that this was a simple case of it being the simplest way to get the desired economic simulation. That is, there was no strong reasoning for having a non-linear mechanic -- it's logical and expected that two mines produce twice as much as one mine. Given that the focus of the game is on core strategy and tactics, there wasn't any compelling justification to model second-order effects of a complex economy.
(The designers could have included an efficiency mechanic that simulates more or less efficiency as the combined network of mines increases... but why bother for this game about skirmishes? It would just be adding complexity where it isn't needed.)
*My suspicion is actually fact, since I designed that particular system
Game Mechanic #3: Victory Points for Routes in Ticket to Ride
Quick Description: In this game, you earn victory points by claiming train routes between different towns. Train routes are claimed by playing enough matching train color cards to fit the route length (e.g. four red train cards to claim a length four red route). Victory Point awards are non-linear for route length -- a length six route awards 15 points whereas a length three route gives only four points.
Graph It!
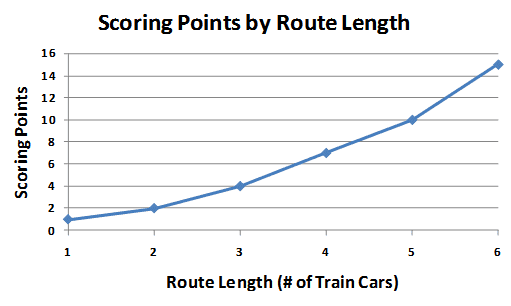
Scoring Points for Different Route Lengths in Ticket to Ride
Dissect It!
Once again, we have a non-linear mechanic breathing down our necks. Claiming a length six route is more than twice as valuable as claiming a length three route. Why do you think the designer chose a non-linear mechanic for this?
While many mechanics are a choice of artistry, I believe in this case that using a non-linear curve is the only real valid decision. This is because of how the game will weaken if the mechanic was linear.
If claiming a length six was only twice as valuable as a length three, or length four vs. length two, then the player has no incentive for claiming the larger routes besides simply needing the route to connect to their destination.
But by having the route lengths award victory points non-linearly, the designer created an additional motivation: if you can manage to save your cards of a given color and claim one of the long routes, it can be a big payoff. This creates opportunities and decisions within the game -- players have a reason to sometimes hold on to their train cards instead of simply spending them whenever a route looks promising. It is a strategy game, after all.
(Note that a length two route is worth exactly twice the points of a length one route. However, claiming a route two is not appreciably harder than a route one, so in this case a nonlinear step was likely unnecessary.)
Game Mechanic #4: Insurance Policies for Starships in Eve Online
Yeah, yeah -- who wants to talk about insurance? But it is in a game, so it's worth discussing because a broken mechanic here isn't much different than a broken mechanic in say, combat.
Quick Description: In Eve online, you can purchase replacement insurance for your starships. If they get destroyed in a valid way (no self-destructs, thank you), the insurance company pays out Interstellar Kredits (ISK) based upon the value of your ship and the level of insurance you purchased.
Graph It!
Here is a sample Insurance Policy choice screen:
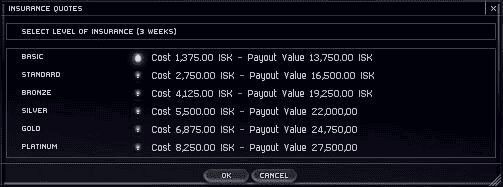
Insurance Policy Options for a Starship in Eve Online
BTW, free insurance covers 40% of the ship value.
Let's graph those numbers. In this case the "domain" (X value) is the purchase cost of the insurance and the payout value is the Y value. The game mechanic, or function, is the behind the scenes link between policy purchase cost and payout value.
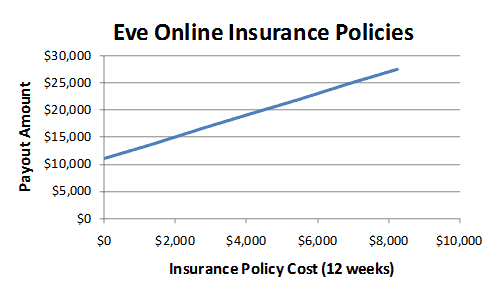
Graph of a Insurance Options for a Starship in Eve Online
Dissect It!
As you can see, the mechanic is linear. Paying nothing gets you insured for 40% of the ship's value. Paying 8,250 for this ship gets you insured for 99% of its value.
Why do you think the developers chose a linear mechanic in this case? What are the advantages or disadvantages of this over a nonlinear insurance schedule?
The starship insurance policies have a 12 week expiration. In what ways does the expiration time affect how the policy costs are structured?
Linearity and non-linearity are core game system design elements I deal with on a daily basis. A simple choice of curve makes a huge difference in everything from control schemes to treasure drops.
Feel free to share any of your favorite mechanics or tips you've encountered in your own design jungle!
Game titles and images are trademark and/or copyright their respective owners. Used for journalistic purposes only.
---
Title photo by Kerri 2009, used under Creative Commons license.
Read more about:
FeaturesYou May Also Like