Trending
Opinion: How will Project 2025 impact game developers?
The Heritage Foundation's manifesto for the possible next administration could do great harm to many, including large portions of the game development community.
This feature takes a look at cellular automation, an algorithmic simulation useful in games, and discusses its use in titles like Minecraft and Dwarf Fortress, as well as other examples, and explains how it can be useful in the context of a game in development.

[This feature takes a look at cellular automation, an algorithmic simulation useful in games, and discusses its use in titles like Minecraft and Dwarf Fortress, as well as other examples, and explains how it can be useful in the context of a game in development.]
What is cellular automation?
My name is John Harris, and I am working on a game called In Profundis (Kickstarter project), that simulates a large cavern world using what is called cellular automation. It allows water to flow, gases to spread, boulders to fall, and other systems propagate and change over time. To perform these feats, it runs a complex system that, each frame, decides on the contents of each cell of a grid-based game world.
Cellular automation is a generally overlooked tool in the game designer's toolbox, but a number of very interesting games have made use of it in one way or another. A partial list: Boulder Dash, SimCity, ADOM, Falling Sand, Dwarf Fortress and Minecraft.
Note those last two, currently darlings of the indie community; both games are popular, at least in part, due to their complex world simulations.
In Profundis uses it in a matter somewhat similar to Dwarf Fortress, although not as complex and in 2D space, as opposed to 3D. (N.B.: I interviewed Tarn Adams, programmer of Dwarf Fortress, for Gamasutra about some of the game's implementation details, including its fluid dynamics.)
By the widest possible definition, cellular automation is a simulation technique that involves performing some operation on the contents of the cells of a regular grid, repeatedly, the results for each cell replacing the previous contents on each pass.
It is a generally overlooked tool for game development for various reasons (we'll get to its drawbacks shortly), but it's been around for some time. The beginning of cellular automation is generally considered to be mathematician John Horton Conway's Game of Life. Life considers the fates of a number of counters on a board who live and die according to a small number of rules.
The player runs the board, seeded with a starting configuration, through a sequence of turns. On each turn, empty spaces with exactly three neighbors experience a birth, and receive a new counter by the next turn. Counters with fewer than two or more than three neighboring counters experience death, and are removed by the next turn. Neighboring spaces are those adjacent either orthogonally or diagonally, thus each space has eight neighbors. And that is all there is to Life.
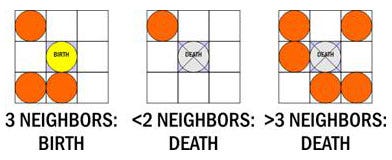
Okay, that is far from all there is to Life. Those are the rules, but cellular automation is an excellent vehicle for illustrating the principle of emergent complexity. Simple patterns with small numbers of counters can explode, over many calculations, and create huge tableaus filling thousands of cells.
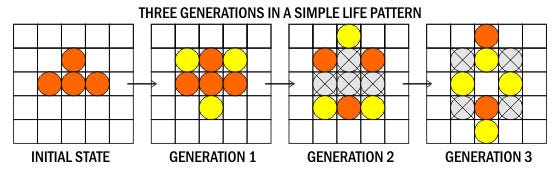
Life's rules are simple, but their consequences have, to this day, yet to be fully explored. (For more information on Life, a good place to start is the Wikipedia page. Also of note are the installments of Martin Gardner's Mathematical Games column in Scientific American, that first publicized the game to the general public. To play around with it yourself, I heartily suggest looking into the open source CA simulator Golly, available for most current platforms.)
While Life can be played without a computer, all the recent discoveries in Life behavior have depended on computer Life simulators. Some of the earliest entertainment software programs written were Life sims.
Not all cellular automation is as deep as Conway's Life. In fact you'd be hard-pressed to come up with a better behavioral-richness to calculation-time ratio. But we don't need elegance of Life's caliber, or anywhere close to it, in order to make good use of cellular automation.
For a game developer, what is useful about cellular automation?
It is great at creating dynamically-changing systems. Flowing liquid is a particularly excellent example. Simulating the spread of lifeforms across a world is another. The spread of fires across a field of fuel is also well suited to CA-driven simulation; both Dwarf Fortress and Minecraft implement interesting (and dangerous) fire spreading behavior.
If designed well, cellular automation takes care of its simulation tasks unobtrusively. You can fairly easily overlay other systems, like a platformer engine, upon the world sim. With a little extra work you could devote the CA process to its own thread, possibly allowing it to be run by its own processor.
Tile-based games are already hosted on a regular, square grid, which naturally suggests a use in cellular automation. In particular, consoles that use hardware tile schemes are well-suited to displaying cellular automation.
Cellular automation systems are not useful in all cases though, and some care must be taken with their use. What must a game developer must be careful about when using cellular automation?
Cellular automation is demanding in both processor time and memory. Every "turn" of the simulation performs a calculation on every square of the grid, which must all be kept in memory.
For 3D simulations this can easily add up to big storage requirements. Minecraft handles it by making the "grain" of its grid quite large; each of its blocks is a meter to a side. If you place a block of water so it flows into a long, complicated channel with many forks the control thread is known to stutter while the water flow is calculated (as of ~1.2). Dwarf Fortress requires lengthy loading and saving processes when starting and finishing sessions, and slows down greatly if many fluids are pouring at once.
With careful design and optimization, the amount of processing can often be greatly reduced, but it is an unavoidable fact that CA-driven simulation is interesting because it allows the world to change dynamically, yet the more changes to the world each turn the more processor time it consumes.
CA is great for simulating changes at its grid size and larger. But because of the coarse nature of the grid (if array is going to be small enough to calculate effectively), and the necessary simplicity of the operations performed in each space, true Newtonian physics simulations are not easy to implement.
For example, falling objects are limited in speed to multiples of the world grid size. It may be possible to cheat around this somewhat, but care must be taken. At the moment however, the sight of pouring liquids is novel enough that great fidelity to the letter of real-world physics isn't normally required.
Some care must be taken that the simulation is carried out evenly; that is to say, that the effects earlier portions of a frame-in-progress do not affect the later calculated portions of that frame. The simplest way to iterate through a cellular world is with nested for loops, iterating in sequence through index variables pointing to each cell of the world array in turn.
But if you use the y loop on the outside and have, say, a rock that falls through space, its position lowered by one y value each x loop, the next y loop may find the rock again in its new home, and cause it to fall again unless you take measures to prevent it. The result: a falling rock seems to teleport instantly to the ground! The same problem can occur on each x loop if the contents of some cells move horizontally.
In Life terms, this is akin to the problem of updating the births or deaths in a cell, but placing those changes immediately into the world grid, where they may affect other births or deaths happening that frame. One way to solve it is to keep a separate world grid handy for recording changes, then swap pointers when a world frame is done, but that has the problem of making it difficult to determine, if you have another thread running that could make changes to the world, which frame to modify. It can also be solved by using special placeholder values to represent births and deaths in progress, which are resolved into real population changes as an extra step.
There are other ways to solve the problem too. I am dubbing this the "partial update" problem. In Profundis uses its own, somewhat hacky, solution, which I describe further below.
CA systems can be difficult to design from scratch. If you're intending to implement real-world physics such as fluid simulation it's not so difficult. More complex use, such as in SimCity which uses it for many purposes, can be daunting.
The difficulty of visualizing the large-scale implications of CA rules means that, to find useful or interesting behavior, you are likely going to have to create prototypes to explore the design space. This makes CA design unfriendly to strict product schedules; you may be better off exploring CA rules on your own time and suggesting its use in a project once you already know of a good ruleset.
CA is sometimes unpredictable! That is part of the appeal, but it can also be trying to level designers. This may be why many CA games use procedural or user-generated content.
This may seem to be a lot of drawbacks, but the advantages are profound, and make possible world simulation with a level of nuance it is difficult to otherwise implement.
While cellular automation must be designed with an eye towards minimizing processor time, it is not necessarily the case that it runs slowly. In Profundis' is fairly complex at it stands, and can handle large amounts of flowing liquid and spreading gas while still maintaining frame rates upwards of 45fps. This, despite the fact that the game engine is currently written in Python, using Psyco for speed!
Additionally, In Profundis' system is designed in such a way that partial frames can be run without sacrificing the integrity of the simulation; each line can be calculated separately, and only a portion of the CA field need be calculated each game frame.
Here is a description of how water is handled in my system. The full system can simulate multiple fluids with different spread rules and densities, but water is an excellent fluid to begin simulating, and can provide interesting game dynamics all by itself.
Each space in the world that contains fluid has a height variable that indicates the amount in the space, from 0 to 8. Let's go over what In Profundis does when its update loop encounters water. (Actually, this isn't exactly what happens -- it's a description of the code from an earlier version of the game. The current version is probably too complex to describe easily.):
First, is the space beneath the current cell empty, or part-full of liquid?
If empty, swap the contents of this space with the contents of the space below, to cause it to "fall" in the game world. We're done with this cell; continue the loop.
If partly full of liquid, how much space is left?
If more than or the same space as liquid, then remove the liquid from this space and add it to that one. We're done.
If less space than liquid, remove as much from this cell as there is space in the lower cell, and add it to the lower cell. Fall through to next case.
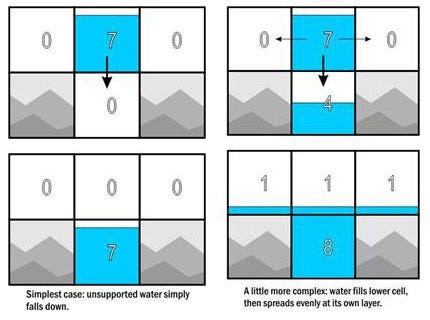
If the lower cell contained a wall or other impassible feature, or it now contains a full cell of fluid, check the left or right sides. Do they have room for fluid?
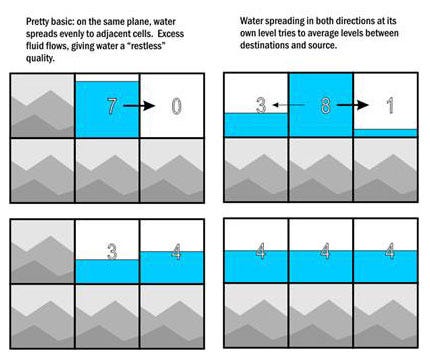
If neither has room, there's nowhere for the fluid to move. We're done.
If only one side is empty, or if the other side has more water than the current one, then we move as much fluid as we can into the emptier side. When we do this, we set a direction flag on that cell, so the next time that cell checks to flow we have a bias direction. This could be considered a flow direction flag. That's important for cases where an odd amount of water wants to flow but must choose between two directions; in the check for direction, the odd unit goes in the bias direction.
This helps water to spread faster, but also gives us a way to have single spaces of water "roam" instead of forming puddles. (There is actually a bug that sometimes prevents this in the current build.) In any case, we find out how much more water is in the current cell than the destination and move half the difference, rounded up.
If both sides have water of lower level than the current one, we attempt to average out the flow so that water levels are the same in all. Ties go to the side in the flow direction, or choose arbitrarily otherwise. We also set each direction's flag.
In all these cases, I also set a nocalc flag on cells water flows into, to prevent cases of water apparently teleporting across the screen if it should get flowing in the direction that we're calculating down the line this world-frame. (For more on this, related to the "partial update" problem mentioned above, see below.)
The takeaway point here is that I covered all the relevant possible situations that a cell containing water could exist in, and just coded what should happen for each one.
I didn't worry about what water should do as a body; I just focused in simulating a little bit of it, and iterated that through the whole screen in a loop.
It is not that complex an algorithm; rarely should good CA code get really windy, since it may be executing hundreds of times a loop. One tries to write simple code, and let all the cells acting together to provide emergent behavior.
This code is, to some extent, a 2D version of Tarn Adams' water flowing system from Dwarf Fortress, and shares one of its flaws: water pressure isn't handled very well. In fact in my game so far, water pressure isn't handled at all; Adams' code simulates it using a bit of a hack to save time.
As a result, water pouring into one side of a U-bend tunnel in my game will currently fail to rise up the other side.
You can watch a video of In Profundis' water simulation by clicking here.
A couple of optimizations my engine uses:
Unlike the similar "Falling Sand" simulation, In Profundis' system calculates tiles, not pixels. While its systems are much more complex, calculation-wise, than Falling Sand's (mostly because of the possibility of multiple types of fluid being in the same cell), each tile is 24 pixels square, producing a tremendous perceived speed advantage compared to Falling Sand.
In Profundis only simulates the portion of the large, scrolling world that's on-screen at the time, plus a small region just outside its borders. In the testbed it is not often that this aspect of the game world becomes visible.
By running some preliminary cycles over the entire world before the simulation begins, allowing the simulation to find equilibrium as fluids find and fill basins, the illusion can be made more complete. The final game will additionally have limited visibility, which will help to further hide the limited nature of updates of the game world.
My solution to the "partial update" problem noted above is unusual. I don't keep a separate copy of the grid. Inspired by some of the work done by hobbyists working on improvements to the Java Falling Sand game, I instead write all changes directly to the grid, reducing memory load and processor overhead. Some special facts of In Profundis' grid help me to avoid the problem:
The y loop iterates from bottom up. This way, falling objects are only "seen" once per loop, so they don't fall multiple times each world-frame.
There is a "do not calculate" flag on each cell. When the contents of a cell other than the current one changes in a given world-frame, the other cell (the one into which the object is being moved) gets its nocalc flag set. When it turns up in a later iteration, if this flag is seen it is cleared then the loop skipped.
This is not the kludge it may seem at first. If you think about it, when two locations are swapped you are really calculating two locations at once, the object you're moving, and the empty space "object" you're moving into its place. The nocalc flag is effectively a way to prevent the new, now-filled space from getting an extra turn. It's something of a kludge, but it is useful in practice.
Even with these considerations, there are still occasional moments where the sequential nature of the loops may cause computational artifacts. These are smoothed out somewhat by alternating left/right direction when I calculate each line, and also alternating every frame. This solution was inspired by the work of the web Falling Sand community, who have created a number of expanded versions of the original Falling Sand game. They are of great interest to anyone seeking to make game use of cellular automation.
Read more about:
FeaturesYou May Also Like