Refractive Texture Mapping, Part Two

Part One of this article investigated the use of sphere mapping to simulate curved-surface reflections. Part Two looks at how refractive texture mapping can be implemented to simulate refractions.

The steps to implement refractive texture mapping are similar to those used in Part One, but instead of figuring out the reflected ray, the refracted ray is computed. These rays are then used to "hit" the texture generating the UV coordinates. The texture doesn't need to be spherical; a simple planar map produces the best results. Finally, the polygons are sent to the hardware to be transformed and rendered. As usual, several details need to be considered for implementation.

Refracted Ray: Is Snell's Law Really Necessary?

The refracted ray (Figure 10) is obtained from the Snell's law that states:

n1*sin (q1) = n2*sin (q2) (Equation 7)
n1 = index of refraction for medium 1 (incident ray)
n2 = index of refraction for medium 1 (refracted ray)
q1= angle between the incident ray and the surface normal
q2= angle between the refracted ray and the surface normal

Figure 10. Refracted ray

I need to share an observation here, because I spent couple of weeks thinking about the problem of the refracted ray. When I realized that I had to use angles to compute the refracted ray, two things entered my mind: first, that it was going to be slow, and second, that the math was going to get complicated. It turned out that computing the refracted ray in 3D space was no exception. As is usual for me, every time I see angles in computer graphics algorithms I don't like it. Among other problems, angles are ambiguous, and normally difficult to work because the algebraic manipulations require special attention with quadrants, conventions, and so on. In spite of my frustration, I finally had an idea: Could I approximate the refracted ray by using another type of calculation rather than Snell's law? Luckily, the answer was yes. There might be several different ways, but here I'll present the one that I came up with that gave me satisfactory results.

Approximating the Refracted Ray

It is possible to approximate the refracted ray by adding the incident ray with the inverted normal and multiplying a factor to the normal. In this article it's called "refraction factor." This refraction factor has nothing to do with the index of refraction (Snell's Law). Indeed the refraction factor is a made up term. What the refraction factor does is to weight the normal's contribution to the final expression. For instance, if the refraction factor is zero, the refracted ray is equal to the incident ray. On the other hand if the refraction factor is a big value, the incident ray's contribution will be so small that the final refracted ray is the inverted normal. By looking at Figure 11 the final expression is:

Figure 11. Approximating the refracted ray

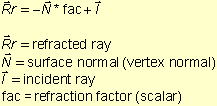
By using Equation 8 to compute the refracted ray, we get rid of angular formulas. Also, because of its nice format, the implementation is straightforward. Figure 12 shows the refracted ray computed by Equation 8 displayed in debug mode.

Figure 12. Refracted ray

"Hitting" The Texture Map

Once the refracted ray has been computed, two more steps are required to get the UV coordinates for rendering. First, the ray needs to be extended to see where it hits the texture map. Second, linear interpolation is used to transform the intersection point to UV coordinates. Note that one more variable is necessary, the depth -- that is, how deep the ray needs to travel until it hits the map. This can be easily done by using the parametric line equation in 3D space. By looking at the line equation we have:

x= x0 + Rfx*t (Equation 9)
y= y0 + Rfy*t
z= z0 + Rfz*t, where:

Rfx, Rfy, Rfz = components of the refracted ray
x, y, z = point of intersection
x0, y0, z0 = initial point
t = parameter

In Equation 9, x0, z0, and y0 are the coordinates of the vertex being processed. Now the program needs to figure out where would be the new XZ coordinates. This can be done by computing the t parameter using the y part of the line equation and the y component from the refracted ray, so that:

y - y0 = Rfy*t,
t = (y - y0) / Rfy (Equation 10)

What is y - y0 exactly? Here is where the variable depth comes into scene. The term y - y0 tells how far down the ray travels, so y - y0 can be replaced by the depth. As y0 is moving up and down throughout the mesh because of the perturbations, the final depth needs to be computed correctly to make sure all the rays stop at the same depth. This is done by adding the initial depth (given variable) plus the displacement between the mesh's initial y and the current vertex. Equation 11 shows how the final t parameter is computed, and Figure 13 a side view of the mesh.

p = pi + (yi - y0)
t = p / Rfy, where: (Equation 11)

p = final depth
pi = initial depth
yi = initial y mesh (mesh without any perturbations)
y0 = current vertex's y component

Figure 13. Intersecting the Map

Once the t parameter has been computed, the z and x part of the line equation is used to compute the ZX intersection. Then, simple linear interpolation is used to transform the new ZX values (intersected point) into UV coordinates. The x-max, x-min, z-max and z-min from the mesh are used for the interpolation. Equation 2 is used, but this time the x-min, x-intersected and x-max values are used to compute the U coordinate. Equally, the z-min, z-intersected z-max values are used to compute the V coordinate. The final equations are:

u, v = texture coordinates
xi = mesh's x minimum value
xe = mesh's x maximum value
zi = mesh's z minimum value
ze = mesh's z maximum value

If we replace xe - xi by the length in the X dimension and ze - zi by the length in the Z dimension we have:

u = (x - xi) / (x_length) (Equation 12)
v = (z - zi) / (z_length), where: (Equation 13)
x_length = xe - xi
z_length = ze - zi

By getting the UV coordinates with these procedures, a problem arises. Depending on the depth and the vertices' positions (especially the ones close to the mesh borders), the refracted ray may not hit the map. What that means is that the intersection region won't be valid, therefore generating or negative UV coordinates, or UV coordinates greater than 1.0. With some hardware, these UV coordinates will make the textures warp, creating undesirable artifacts.

A few things can be done to correct this problem. The simplest way is just to clamp the UV values if they are invalid. Some "ifs" can be added to the inner loop checking for invalid UV coordinates, for example, if they are negative they are clamped to 0 and if they go over 1 they are clamped to 1. This procedure can still generate undesirable artifacts, but depending on the camera position and the texture, it may not be too noticeable. Another way is to figure out what would be the maximum and minimum X and Z values the refracted ray can generate at the corners of the mesh (with the maximum angle). Then you can change the interpolation limits taking into account this fact. Now, instead of interpolating the UV from 0 to 1, let's say for example they would go from 0.1 to 0.9. By doing this, even when the X and Z values extrapolate the limits, the UV coordinates are still in range. My sample program uses the first approach, and Listing 4 shows the implementation of refractive texture mapping.

Second Simulation Using Refractive Texture Mapping

The implementation of the simulation with refractive texture mapping is straightforward, but in this case the render function needs to call the refraction function (Listing 4) instead of the reflection function . There is one more detail needs to be observed, the V coordinate calculations are flipped in Listing 4, because the UV conventions that DirectX 7 (and most libraries) uses do not match the way the Z coordinate is used in the interpolation. This is not a big problem, but if the V coordinate is computed exactly as in Equation 13, the texture will look inverted. Figure 14 shows the final mesh rendered with a few perturbations and refractive texture mapping (note the clamping problem on the lower border of the mesh), and Figure 15 shows the texture used.

Figure 14 (top): Refractive texture mapping Figure 15 (bottom): Texture used in Figure 14

Listing 4. Refractive texture mapping and perturbations

void water_compute_refraction (WATER *water)
{

DEBUG_FATAL_ERROR (!water);

//update camera
camera = TransformD3DCamera;

// x_length is equal xe-xi
interpolation_factor_x= 1.0f/(water->initial_parameters.x_length);
xi = water->initial_parameters.x0;

// z length is equal ze-zi
// to make the z convention match with the v coordinates we need to flip it
interpolation_factor_z = -1.0f/(water->initial_parameters.z_length);
ze = water->initial_parameters.z0+water->initial_parameters.z_length;

//loop through the vertex list
vertex_current = (VERTEX_TEXTURE_LIGHT *)water->mesh_info.vertex_list;
for (t0=0; t0mesh_info.vertex_list_count; t0++, vertex_current++)
{

//get incident ray
camera_ray.x = camera.camera_pos.x - vertex_current->x;
camera_ray.y = camera.camera_pos.y - vertex_current->y;
camera_ray.z = camera.camera_pos.z - vertex_current->z;

//avoid round off errors
math2_normalize_vector (&camera_ray);

vertex_normal.x = vertex_current->nx;
vertex_normal.y = vertex_current->ny;
vertex_normal.z = vertex_current->nz;

//compute the approx refracted ray
refracted_ray.x = -(vertex_normal.x*water->refraction_coeff + camera_ray.x);
refracted_ray.y = -(vertex_normal.y*water->refraction_coeff + camera_ray.y);
refracted_ray.z = -(vertex_normal.z*water->refraction_coeff + camera_ray.z);

math2_normalize_vector (&refracted_ray);

//let's compute the intersection with the planar map
final_depth = water->depth+(vertex_current->y-water->initial_parameters.y0);
t = final_depth/refracted_ray.y;

//figure out the hitting region
map_x = vertex_current->x + refracted_ray.x*t;
map_z = vertex_current->z + refracted_ray.z*t;

//interpolate
new_u = (map_x-xi)*interpolation_factor_x;

//because of variable conventions the z/v is flipped
new_v = (map_z-ze)*interpolation_factor_z;

//clamp if overflow
if (new_u < water->refraction_uv_min) new_u = water->refraction_uv_min;
if (new_u > water->refraction_uv_max) new_u = water->refraction_uv_max;

if (new_v < water->refraction_uv_min) new_v = water->refraction_uv_min;
if (new_v > water->refraction_uv_max) new_v = water->refraction_uv_max;

//assign
vertex_current->u = new_u;
vertex_current->v = new_v;

 

} //end main loop

Optimizations

Some optimizations can be done to the techniques described in this article to speed up the calculations. Nevertheless, I have to admit that water simulation done by these techniques can be intense if the mesh is composed of a lot of polygons, especially because the vertex data changes every frame. Your best bet is not to use too many polygons, but I'll go over some of the bottlenecks here.

In the mapping techniques, most of the calculations rely on vector normalization. I did not address this problem too much because most console platforms perform vector normalization in hardware, and on PCs the new Pentiums can handle square roots reasonably well.

Perhaps where a lot of experimentation can be done is in the perturbations. As I mentioned earlier, instead of use the ripple equation, you can try to replace this part by the array algorithm (see References) or a spring model. However; it's important to know that these algorithms do not use sine waves and therefore the ripples may lose their round shape (in side view). I haven't tried this yet, but it will definitely speed up the code. If you plan to use the ripple equation anyway, another thing that can be done is to create a big square root lookup table. That is, if the ripples are always generated certain positions, the radius

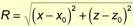
can be precomputed and stored in an array. Even though the values under the square root are floats, the mesh is composed of discrete points. Using this fact, you can use the vertices' indices to index the square root array.

Another big bottleneck in the code is the normal calculation. Here more than anywhere else I welcome reader suggestions, because I could not find a very efficient way of computing the vertex normals for a mesh that's constantly being morphed. They way I've implemented it is to create lookup tables of neighboring triangles. When I loop through the mesh vertices I can quickly look up its neighboring faces and average these face normals. However, this is still slow, and even console hardware won't be able to help me much, except for the vector normalization.

Sample Program

When you look at my implementation, you'll notice that the code is slightly different from the code presented in this article. There is a lot of debugging code, editor interface variables, as well as some experiments I was doing. In this article, I excluded this part for sake of clarity. Also, you won't be able to download the whole application source files to compile in your computer. I just put the water part for you to look at as a reference. The main reason for this is because the water implementation is part of an editor I've been working on for the past two years or so. The whole editor has thousands of lines of code, and it performs several different algorithms, experiments, and so on. So, I decided to not make the entire editor public. If you run the editor, you can control several parameters of the mesh, mapping techniques, and perturbations. You can play around with those parameters to see how they affect the final simulation. Also, you can fly with the camera by using arrows, A, Z, Q, W, and Shift and Control plus these keys will make the camera move slower or strafe.

Final Words

I hope this information has helped you to understand and implement some interesting techniques for simple water simulation using refractive texture mapping. Please e-mail me at [email protected] or [email protected] with suggestions, questions, or comments.

To download the code and run the sample application, go to my web site at www.guitarv.com, and you should find everything you need under "Downloads."

References

Möller, Tomas, and Eric Haines. Real-Time Rendering. A.K. Peteres, 1999. pp 131-133.

Direct X 7 SDK Help (Microsoft Corp.)

Serway, R. Physics for Scientists and Engineers with Modern Phyisics, 4th ed. HBJ, 1996. pp. 1023-1036.

Ts'o, Pauline, and Brian Barsky. "Modeling and Rendering Waves: Wave-Tracing Using Beta-Splines and Reflective and Refractive Texture Mapping." SIGGRAPH 1987. pp. 191-214.

Watt, Alan, and Fabio Policarpo. The Computer Image. Addison-Wesley, 1997. pp. 447-448.

Watt, Alan, and Mark Watt. Advanced Animation and Rendering Techniques: Theory and Practice. Addison-Wesley, 1992. pp. 189-190

Harris, John W., and Horst Stocker. Handbook of Mathematics and Computational Science. Springer Verlag, 1998.

PlayStation Technical Reference Release 2.2, August 1998 (Sony Computer Entertainment)

Elias, Hugo. http://freespace.virgin.net/hugo.elias/graphics/x_water.htm

Lander, Jeff. "A Clean Start: Washing Away the New Millennium." Game Developer (December 1999) pp. 23-28.

Haberman, Richard. Elementary Applied Partial Differential Equations, 3rd ed. Prentice Hall, 1997. pp. 130-150.

Graff, Karl F. Wave Motion In Elastic Solids. Dover Publications, 1991. pp. 213-272.