Inexpensive Underwater Caustics Using Cg

Author: by Daniel Sánchez-Crespo Dalmau

There's something hypnotic about the way water interacts with light: the subtle reflections and refractions, the way light bends to form dancing light patterns on the bottom of the sea, and the infinitely-varied look of the ocean surface. These phenomena and their complexity have attracted many researchers from the physics field and, in recent years, the computer graphics arena. Simulating and rendering realistic water is, like simulating fire, a fascinating task: it is not easy to achieve good results at interactive frame rates, and thus creative thinking must often be used.

This article explains an aesthetics-driven method for rendering the underwater lighting effects known as "caustics" in real-time. We believe the technique is fully original, and has very low computational cost. It is a purely aesthetics-driven approach, and thus realism is simply out of consideration: we try to create something that looks good, not something that is right from a simulation standpoint. As we will soon see, results look remarkably realistic, and the method can easily be implemented in most graphics hardware. This simplified approach has proven very successful in many fractal-related disciplines, such as mountain and cloud rendering or tree modeling.

The purpose of this article is twofold. First, it tries to expose a new technique, from its physical foundations to the implementation details. As the technique is procedural, it yields elegantly to a shader-based implementation. Thus, a second objective is to showcase the conversion from regular OpenGL code to an implementation using the Cg programming language. This article should then satisfy both those interested in water rendering algorithms, as well as those wanting an introduction to pixel shader programming in Cg.

Computing Caustics

Computing underwater caustics accurately is a complex process: millions of individual photons are involved, with many interactions taking place. To simulate it properly, we must begin by shooting photons from the light source (for a sea scene, the sun). A fraction of these photons eventually collide with the ocean surface, either reflecting or refracting themselves. Let's forget about reflection for a second, and see how refracted photons bend their trajectory according to Snell's Law, which states that:

sin (incoming)/sin (refracted) = IOR

The formulation above makes only one restriction, and thus is not very convenient as a way to compute the refracted ray. Assuming the incident, transmitted and surface normal rays must be co-planar, a variety of coder-friendly formulas can be used, such as the one explained in Foley & VanDam's book[1]:

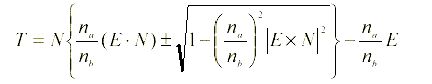
Here T is the transmitted ray, N is the surface normal, E is the incident ray, and na, nb are the incides of the refraction.

Once bent, photons advance through the water, their intensity attenuating as they reach deeper. Eventually, part of those photons will strike the ocean floor, lighting it. As the ocean's surface was wavy, photons following different paths can end up lighting the same area. Whenever this happens, we see a bright spot which is a caustic created by the light concentrating, in a similar way that a lens can burn a piece of paper.

From a simulation standpoint, caustics are usually computed by either forward or backwards ray tracing. In forward ray tracing, photons are sent from light sources and followed through the scene, accumulating their contribution over discrete areas of the ground. The problem with this approach is that many photons do not even collide with the ocean surface and, from those that actually collide with it, very few actually contribute to caustic formation. Thus, it is a brute-force method, even with some speed-ups thanks to spatial subdivision.

Backwards ray-tracing works on the opposite direction. It begins at the ocean floor, and traces rays backwards in reverse chronological order, trying to compute the sum of all incoming lighting for a given point. Ideally, this would be achieved by solving the semi-spherical integral of all light coming from above the point being lit. Still, for practical reasons the result of the integral is resolved via Monte Carlo sampling. Thus, a beam of candidate rays is sent in all directions over the hemisphere centered at the sampling point. Those that hit other objects (such as a whale, ship or stone) are discarded. On the other hand, rays that hit the ocean surface definitely came from the outside, making them good candidate. Thus, they must be refracted, using the inverse of Snell's Law. These remaining rays must be propagated in the air, to test whether that hypothetic ray actually emanated from a light source, or was simply a false hypothesis. Again, only those rays that actually end up hitting a light source do contribute to the caustic, and the rest of the rays are just discarded as false hypothesis.

Both approaches are thus very costly: only a tiny portion of the computation time actually contributes to the end result. In commercial caustic processors it is common to see ratios of useful vs. total rays between 1 and 5%.

Real-time caustics were first explored by and Jos Stam [2]. Their approach involved computing an animated caustic texture using wave theory, so it can be used to light the ground floor. This texture was additively blended with the object's base textures, giving a nice convincing look.

Another interesting approach was explored by Lasse Staff Jensen and Robert Golias in their excellent Gamasutra paper [3]. The paper covers not only caustics, but a complete water animation and rendering framework. The platform is based upon Fast Fourier Transforms (FFTs) for wave function modeling. On top of that, it handles reflection, refraction, and caustics attempting to reach physically-accurate models for each one. It is unsurprising, then, that their approach to caustics tries to model the actual process: rays are traced from the Sun to each vertex in the wave mesh. Those rays are refracted using Snell's Law, and thus new rays are created.

Our Approach

The algorithm we use to simulate underwater caustics is just a simplification of the backwards Monte Carlo ray tracing idea explained above. We make some aggressive assumptions on good candidates for caustics, and thus compute only a subset of the arriving rays. Thus, the method has very low computational cost, and produces something that, while being totally incorrect from a physical standpoint, very closely resembles a caustic's look and behavior.

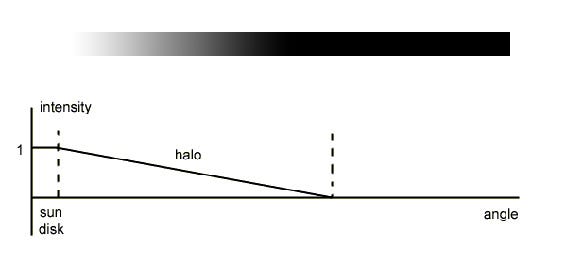
To begin with, we shall assume we are computing caustics at noon in the Equator. This implies the sun is directly above us. For the sake of our algorithm, we will need to compute the angle of the sky covered by the sun disk. The sun is between 147 and 152 million kilometers away from Earth depending on the time of the year, and its diameter is 1,42 million kilometers. Half a page of algebra and trigonometry yield an angle for the Sun disk of 0.53º. Still, the Sun is surrounded by a very bright halo, which can be considered as a secondary light source. The area covered by the halo is about ten times larger than the Sun itself.

The second assumption we shall make is that the ocean floor is located at a constant depth-usually relatively shallow. The transparency of water is between 77 and 80% per linear meter. This means that between 20 and 23% of incident light per meter is absorbed by the medium (heating it up), giving a total visibility range between fifteen and twenty meters. Logically, this means caustics will be formed most easily when light rays travel the shortest distance from the moment they enter the water to the moment they hit the ocean floor. Thus, caustics will be maximal for vertical rays, and will not be so visible for rays entering water sideways. This is an aggressive assumption, but is key to the success of the algorithm.

Then, our algorithm works as follows: we start at the bottom of the sea, right after we have painted the ground plane. A second additive, blended pass is used to render the caustic on top of that. To do so, we create a mesh with the same granularity as the wave mesh, and which will be colored per-vertex with the caustic value: zero means no lighting, one means a beam of very focused light hit the sea bottom. To construct this lighting, backwards ray tracing is used: for each vertex of the said mesh, we project it vertically until we reach the wave point located right on top of it. Then, we compute the normal of the wave at that point using finite differences. With the vector and the normal, and using Snell's Law (remember the IOR for water is 1.33333) we can create secondary rays, which travel from the wave into the air. These rays are potential candidates for bringing illumination onto the ocean floor. To test them, we compute the angle between them and the vertical. As the Sun disk is very far away, we can simply use this angle as a measure of illumination: the closer to the vertical, the more light that comes from that direction into the ocean.

Implementation Using OpenGL

The initial implementation of the algorithm is just plain OpenGL code with the only exception being the use of multipass texturing. A first pass renders the ocean floor as a regular textured quad. Then, the same floor is painted again using a fine mesh, which is lit per-vertex using our caustic generator as can be seen in the figures. For each vertex in the fine mesh, we shoot a ray vertically, collide it with the ocean surface, generate the bent ray using Snell's Law, and use that ray to perform a texture map lookup, such as the one in figure 2. In the end, the operation is not very different from a planar environment mapping pass. The third and final pass renders the ocean waves using our waveform generator. These triangles will be applied a planar environment mapping, so we get a nice sky reflection on them. Other effects such as Fresnel's equation can be implemented as well on top of that. Here is the full pseudo-code for this version:

Paint ocean floor
For each vertex in the fine mesh
   Send a vertical ray
   Collide the ray with the ocean's mesh
   Compute the refracted ray using Snell's law reversed
   Use the refracted ray to compute texturing coordinates on the "sun" map
   Apply textured coordinates to vertex in finer mesh
End for
Render ocean

Implementation Using Cg

Cg allows us to move all these computations to the GPU, using a C-like syntax. In fact, the same wave function previously executed on the CPU was simply copied into the pixel and vertex shaders using an include file, with only minor modifications to accommodate the vector-based structures in Cg.

Calculating the caustics per-pixel instead of per-vertex improves the overall visual quality and decouples the effect from geometric complexity. We considered two approaches when porting the technique to the GPU's pixel shaders-both use the partial derivatives of the wave function to generate a normal, unlike the original method which relies on finite differences.

The first method takes advantage of the fact that a procedural texture can be rendered in screen space, thereby saving render time when only a small portion of the pixels are visible. Unfortunately, this also means that when a large number of pixels are visible a lot of work is being done for each one, even though the added detail may not be appreciable. Sometimes this large amount of work can slow down the framerate enough to be undesirable, so another method is needed to overcome this limitation.

The second method renders in texture space to a fixed resolution render target. Although rendering in texture space has the advantage of maintaining a constant workload at every frame, the benefit of only rendering visible pixels is lost. Additionally, it becomes difficult to gauge what render target resolution most adequately suits the current scene, to the point where relying on texture filtering may introduce the tell-tale bilinear filtering cross pattern if the texel to pixel ratio drops too low.

As decribed earlier, the effect calculates the normal of the wave function to trace the path of the ray to the intercept point on a plane, or the ocean surface in this example. To generate the normal, the partial derivatives of the wave function, in x and y, can easily be found using the chain and product rules, as found in elementary calculus texts. Let's quickly review these rules.

If a function f(x) can be written as f(x)=f(g(x)), then the chain rule states that its derivative with respect to x is given, in Leibniz notation, as

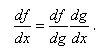
The product rule is given as

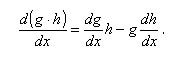
Let's write the wave function used in the original approach as

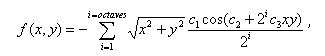
where i indicates the number of octaves used to generate the wave, c₁, c₂ and c₃ are constants to give the wave shape and size, and x and y range from 0 to 1, inclusive, and indicate a point on a plane at a fixed height.

Therefore, to calculate the partial derivates in x and y of the wave function, we let and , where 2ⁱ is treated as a constant.

Applying the chain and product rules yield two functions, the partial derivatives, which are written as

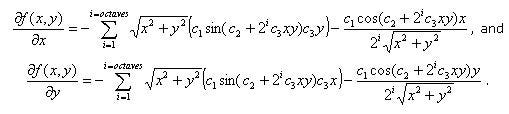
Note that c₁ can be factored outside the summation.

The partial derivatives are actually components of the gradient vector at the point where they are evaluated. As the function actually represents height, or z, the partial derivative with respect to z is simply 1. The normal is then

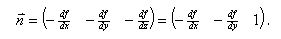
The last equation required to render the caustics is the line-plane intercept. We can calculate the distance from a point on a line to the interception point on the plane using the following formula:

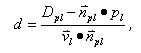
where D_pl is the distance from the plane to the origin, n_pl is the normal of the plane, p_l is a point on the line, and v_l is the vector describing the direction of the line, namely the normal we calculated above.

Evidently the new calculations done per pixel are quite complex, but given the flexibility of higher level shading languages and the pixel processing power available in current generation hardware devices, they are trivial to implement and quick to render. The sample code below shows the implementation in Cg.

Once we have calculated the interception point we can use this to fetch into our caustic light map using a dependent texture read, and then add the caustic contribution to our ground texture, as shown in the following code sample.

The results in Figures 3a and 3b show the quality improvement achieved by doing the calculations per pixel instead of per vertex. As can be seen, a sufficiently large resolution texture has as good quality as screen space rendering, without the performance impact when large numbers of pixels are displayed. Additionally, when using a render target texture, we can take advantage of automatic mipmap generation and anisotropic filtering to reduce aliasing of the caustics, which cannot be done when rendering to screen space.

Conclusions And Future Work

The algorithm we have exposed shows a simple, alternative way to tackle an otherwise complex issue such as caustic simulation. Additionally, this article has tried to show how a classic algorithm can be upgraded and enhanced to take advantage of shader-based techniques, which are becoming more important these days. As future work, we'd like to extend the technique so it can work on non-horizontal ground planes, so it can be used to illuminate a submarine below the water, for example. As shader processing power increases, we hope soon we will be able to directly implement the full Monte-Carlo approach on the shader, and thus compute caustics realistically in real-time.

Another technique we would like to experiment with is incorporating so called "god rays" (very focused light beams through water) to the solution, so a complete, aesthetically pleasing model for underwater rendering using shaders can be described.

I would like to thank Juan Guardado of Nvidia Corporation for helping with the Cg implementation and providing feedback on this algorithm. I would also like to thank everyone at Universitat Pompeu Fabra for their continued support.

Demos

Caustics - No Shader

Cg Caustics

Bibliography

[1] Foley, van Dam, Feiner and Huges. Computer Graphics. Principles and Practice. ISBN 0-201-84840-6
[2] "Random Caustics: Natural Textures and Wave Theory Revisited", Technical Sketch SIGGRAPH'96. In ACM SIGGRAPH Visual Proceedings, 1996, p. 151.
[3] Lasse Staff Jensen, Robert Golias. Deep water animation and rendering,
http://www.gamasutra.com/gdce/2001/jensen/jensen_01.htm
[4] An introduction to Ray Tracing, Glassner, A. S. (editor), Academic Press, 1989

______________________________________________________