Implementing Lighting Models With HLSL
Pixel and vertex shaders are well suited for dynamically lighting scenes. In this article, Engel demonstrates how to implement common lighting formulas using the High Level Shader Language (HLSL) that DirectX 9 supports.

With the introduction of the second generation of shader-capable hardware like the ATI Radeon 9500 (and more recent boards) and the Nvidia GeForce FX, several high-level languages for shader programming were released to the public. Prior to this hardware support, shader programming was performed exclusively with assembly-like syntax, that was difficult to read for a non-assembly programmer. The new C-like languages make learning shader programming faster and make the shader code easier to read.
The new shader languages -- Cg, HLSL and GLslang -- have similar syntax and provide similar functionality. Continuing Gamasutra's series on shader programming (which began with "Animation Using Cg" by Mark Kilgard and Randy Fernando), I will look at using the High Level Shader Language (HLSL) which comes with DirectX 9. However, the examples I provide should run without any changes in a Cg environment and with only minor changes in a GLslang environment. For further rapid prototyping of these shaders, ATI's RenderMonkey is highly recommended. The code and executables for all of the examples presented in this article can be downloaded in a single file called "gamasutra-hlsl-lighting-examples.zip" (17MB). (Editor's note: the file is no longer available.)
Getting a Jump Start with HLSL
The only requirement to start HLSL programming with the DirectX SDK is that the HLSL compiler is installed properly. This is done by setting the right directory path in the Tools>Option>Project>VC++ Directories of the Visual .NET IDE. Additionally the shader debugger provided for Visual .NET (not Visual C/C++ 6) should be installed from the SDK CD-ROM. This installation is optional and has to be explicitely chosen therefore. To be able to use the Visual Studio .NET shader debugger, the following steps are necessary:
Install the shader debugger. This is an option in the DirectX 9 SDK installation routine, which must be selected.
Select the "Use Debug Version of Direct3D" and "Enable Shader Debugger" check boxes in the configuration panel of the DirectX run-time.
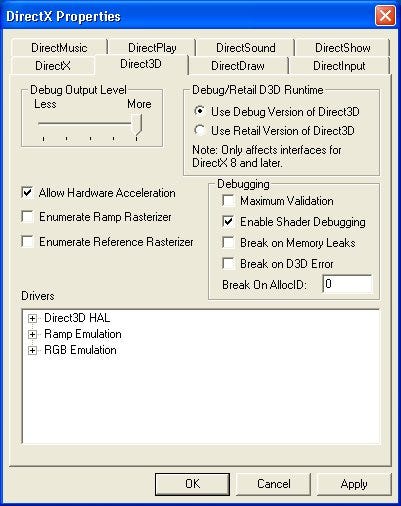
Figure 1. The Direct3D properties box. This checkbox can be found at Start>Control Panel>DirectX and there on the Direct3D tab.
Launch the application under Visual Studio .NET with Debug>Direct3D>Start D3D
Switch to the reference rasterizer
Set a breakpoint in Vertex Shader or Pixel Shader
Shader assembly can be viewed under Debug>Window>Disassembly
Render targets can be viewed under Debug>Direct3D>RenderTarget
Tasks of the Vertex and Pixel Shader
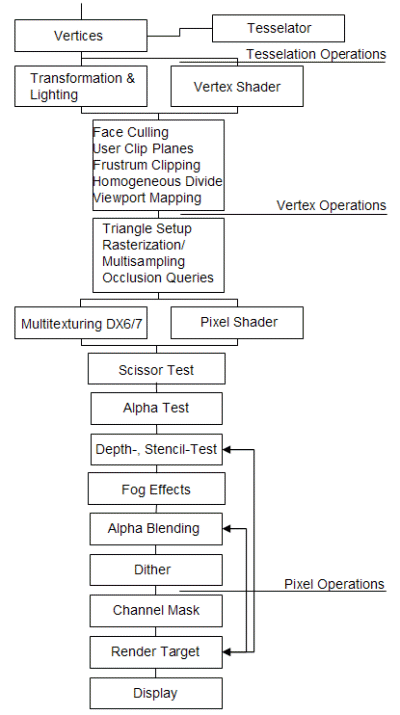
To estimate the capabilities of vertex and pixel shaders, it is helpful to look at their position in the Direct3D pipeline
| ||
Figure 2. The Direct3D pipeline. |
The vertex shader, as the functional replacement of the legacy transform and lighting stage (T&L), is located after the tesselation stage and before the culling and clipping stages. The data for one vertex is provided by the tesselation stage to the vertex shader. This vertex might consist of data regarding its position, texture coordinates, vertex colors, normals and so on.
The vertex shader can not create or remove a vertex. Its minimal output value is the position data of one vertex. It can not affect subsequent stages of the Direct3D pipeline.
The pixel shader, as the functional replacement of the legacy multitexturing stage, is located after the rasterizer stage. It gets its data from the rasterizer, from the vertex shader, from the application and from texture maps. It is important to note here that texture maps can not only store color data, but all kinds of numbers that are useful to calculate algorithms in the pixel shader. Furthermore, the result of the pixel shader can be written into a render target and set in a second rendering pass as the input texture. This is called "render to render rarget". The output of the pixel shader consists usually of a float4 value. In a case where the pixel shader renders in several render targets at once, the output might be up to four float4 values (Multiple Render Targets; MRT).
With the help of the pixel shader, subsequent stages of the Direct3D pipeline can be "influenced" by choosing for example a specific alpha value and configuring the alpha test or alpha blending in a specific way.
Common Lighting Formulas Implemented with HLSL
To demonstrate the use of HLSL to create shaders, and to demonstrate the tasks of the vertex and pixel shaders, the following examples show the implementation of the common lighting formulas (for a more extensive introduction read [Mitchell/Peeper]).
Ambient Lighting
In an ambient lighting model, all light beams fall uniformly from all directions onto an object. A lighting model like this is also called a "global lighting model" (an example of a more advanced global lighting model is called "area lighting"). The ambient lighting component is usually described with the following formula:
I = Aintensity * Acolor
The intesity value describes the lighting intensity and the color value describes the color of the light. A more complex lighting formula with its ambient terms might look like this:
I = Aintensity * Acolor + Diffuse + Specular
The diffuse and specular component are placeholders here for the diffuse and specular lighting formulas that will be described in the upcoming examples. All high-level languages support shader instructions that are written similar to mathematical expressions like multiplication, addition and so on. Therefore the ambient component can be written in a high-level language as follows:
float4 Acolor = {1.0, 0.15, 0.15, 1.0};
float Aintensity = 0.5;
return Aintensity * Acolor;
A simplified implementation might look like this:
return float4 (0.5, 0.075, 0.075, 1.0);
It's common to pre-bake the intensity values and the color values into one value. This is done in the following example programs for simplicity and readability, otherwise the HLSL compiler would pre-bake the two constant values together in its output. The following source code shows a vertex and a pixel shader that displays ambient lighting:
struct VS_OUTPUT VS_OUTPUT VS( float4 Pos: POSITION ) float4 PS() : COLOR | ||
|
The structure VS_OUTPUT at the beginning of the source describes the output values of the vertex shader. The vertex shader looks like a C function with the return value VS_OUTPUT and the input value in the variable Pos in brackets after its name VS.
The input and output values for the vertex shader use the semantic POSITION, which is identified by a colon (:) that precedes it. Semantics help the HLSL compiler to bind the right shader registers for the data. The semantic in the vertex shader input structure identifies the input data to the function as position data. The second semantic indentifies the vertex shader return value as position data that will be an input value to the pixel shader (this is the only obligatory output value of the vertex shader). There are several other semantics for the vertex shader input data, vertex shader output data, pixel shader input data and pixel shader output data. The following examples will show a few of them (consult the DirectX 9 documentation for more information).
Inside the brackets, the vertex shader transforms the vertex position with the matWorldViewProj matrix provided by the application as a constant and outputs the position values.
The pixel shader follows the same C-function-like approach as the vertex shader. Its return value is always float4 and this value is always treated as a color value by the compiler, because it is marked with the semantic COLOR. Unlike to the vertex shader, the pixel shader takes no explicit input value here (except the obligatory POSITION), because the brackets after its name PS are empty.
The names of the vertex and pixel shader are also the entry point for the high-level language compiler and must be provided in its command line.
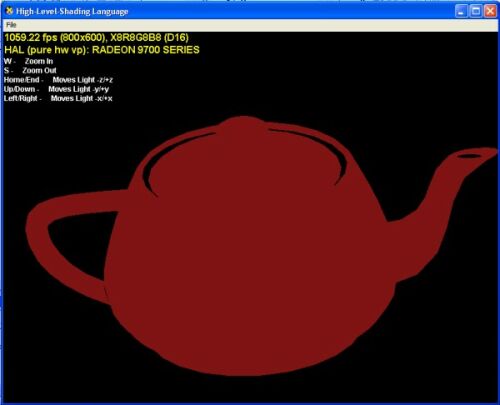
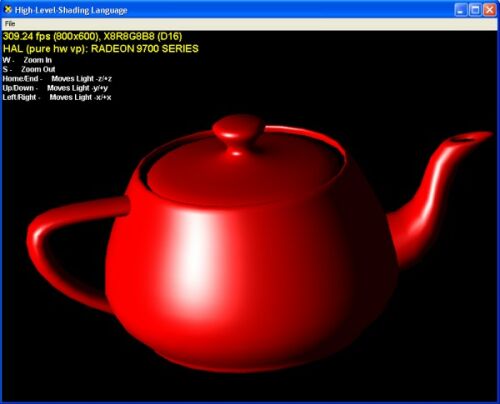
The following screenshot shows the example program with an ambient lighting model:
| ||
Figure 3. Ambient lighting. |
The knob of the top of the teapot is not visible, when it is turned towards the viewer. This is because all light beams are coming from all directions uniformly onto the object, and therefore the whole teapot gets exactly the same color.
Diffuse Lighting
In a diffuse lighting model (or "positional lighting model") the location of the light is considered. Another characteristic of diffuse lighting is that reflections are independent of the observer's position. Therefore the surface of an object in a diffuse lighting model reflects equally well in all directions. This is why diffuse lighting is commonly used to simulate matte surfaces (another more advanced lighting model to simulate matte surfaces was developed by Oren-Nayar [Fosner] [Valient]).
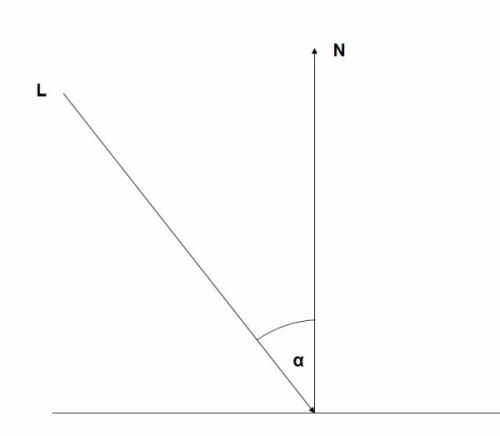
The diffuse lighting model following Lambert's law is described with the help of two vectors (read more in [RTR] and [Savchenko]). The light vector L describes the position of light and the normal vector N describes the normal of a vertex of the object.
The diffuse reflection has its peak (cos alpha = = 1) when L and N are aligned; in other words, when the surface is perpendicular to the light beam. The diffuse reflection diminishes for smaller angles. Therefore light intensity is directly proportional to cos a.
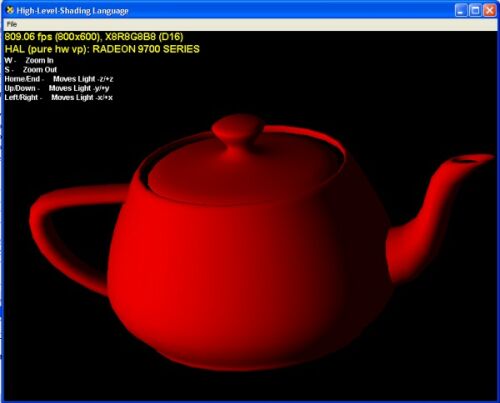
| ||
Figure 4. Diffuse lighting. |
| ||
Figure 5. Light and normal vector. |
To implement the diffuse reflection in an efficient way, a property of the dot product of two n-dimensional vectors is used:
N.L = ||N|| * ||L|| * cos alpha
If the light and normal vectors are of unit length (normalized), this leads to
N.L = cos alpha
When N.L is equal to cos alpha , the diffuse lighting component can be described with the dot product of N and L. This diffuse lighting component is usually added to the ambient lighting component like this:
I = Aintensity * Acolor + Dintensity * Dcolor * N.L + Specular
The example uses the following simplified version:
I = A + D * N.L + Specular
The following source code shows the HLSL vertex and pixel shaders:
struct VS_OUTPUT VS_OUTPUT VS(float4 Pos : POSITION, float3 Normal : NORMAL) float4 PS(float3 Light: TEXCOORD0, float3 Norm : TEXCOORD1) : COLOR | ||
|
Compared to the previous example, the vertex shader gets additionally a vertex normal as input data. The semantic NORMAL shows the compiler how to bind the data to the vertex shader registers. The world-view-projection matrix, the world matrix and the light vector are provided to the vertex shader via the constants matWorldViewProj, matWorld, vecLightDir. All these constants are provided by the application to the vertex shader.
The vertex shader VS outputs additionally the N and L vectors in the variables Light and Norm here. Both vectors are normalized in the vertex shader with the intrinsic function normalize(). This function returns the normalized vector v = v/length(v). If the length of v is 0, the result is indefinite.
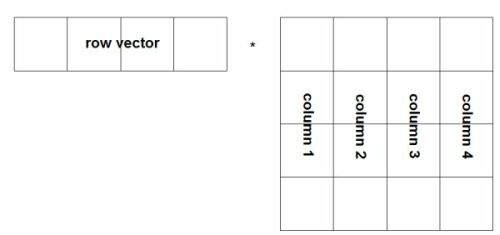
The normal vector is transformed by beeing multiplied with the world matrix (read more on transformation of normals in [RTR2]). This is done with the function mul(a, b), which performs a matrix multiplication between a and b. If a is a vector, it is treated as a row vector. If b is a vector, it is treated as a column vector. The inner dimensions acolumns and brows must be equal. The result has the dimension arows * bcolumns. In this example mul() gets the position vector as the first parameter --therefore it is treated as a row vector -- and the transformation matrix, consisting of 16 floating-point values (float4x4), as the second parameter. The following figure shows the row vector and the matrix:
| ||
Figure 6. Column-major matrix multiply. |
The whole lighting formula consisting of an ambient and a diffuse component is implemented in the return statement. The diffuse and ambient constant values were defined in the pixel shader to make the source code easier to understand. In a real-world application these values might be loaded from the 3D model file.
Specular Lighting
Whereas diffuse lighting considers the location of the light vector and ambient lighting does not consider the location of the light or the viewer at all, specular lighting considers the location of the viewer. Specular lighting is used to simulate smooth, shiny and/or polished surfaces.
| ||
Figure 7. Phong lighting |
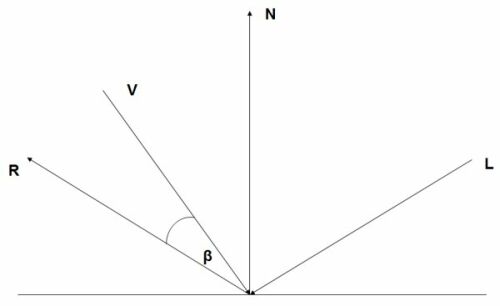
In the specular lighting model developed by Bui Tong Phong [Foley], two vectors are used to calculate the specular component: the viewer vector V that describes the direction of the viewer (in other words the camera), and the reflection vector R that describes the direction of the reflections from the light vector.
| ||
Figure 8. Vectors for specular lighting. |
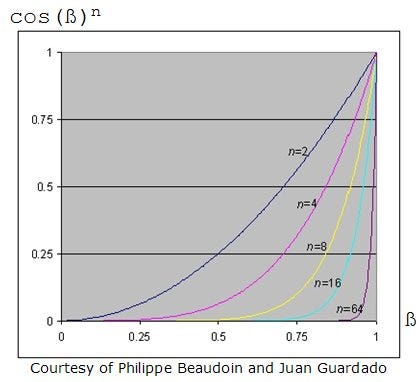
The angle between V and R is ß. The more V is aligned with R, the brighter the specular light should be. Therefore cos ß can be used to describe the specular reflection. Additionally to characterize shiny properties an exponentn is used.
| ||
Figure 9. Specular power value. |
Therefore the specular reflection can be described with
cos (ß)n
In an implementation of a specular lighting model, a property of the dot product can be used as follows:
R.V = ||R|| * ||V|| * cos ß
If both vectors are of unit length, R.V can replace cos ß. Therefore the specular reflection can be described with
(R.V)n
It is quite common to calculate the reflection vector with the following formula (read more in [Foley2]):
R = 2 * (N.L) * N - L
The whole Phong specular lighting formula now looks like this:
I = Aintensity * Acolor + Dintensity * Dcolor * N.L + Sintensity * Scolor * (R.V)n
Baking some values together and using white as the specular color leads to (find a more advanced implementation of specular lighting together with cube map shadow mapping at [Persson] [Valient]):
I = A + D * N.L + (R.V)n
The following source shows the implementation of the Phong specular lighting model:
struct VS_OUTPUT VS_OUTPUT VS(float4 Pos : POSITION, float3 Normal : NORMAL) float4 PS(float3 Light: TEXCOORD0, float3 Norm : TEXCOORD1, // I = Acolor + Dcolor * N.L + (R.V)n | ||
|
Like the previous example, the vertex shader input values are the position values and a normal vector. Additionally, the vertex shader gets as constants the matWorldViewProj matrix, the matWorld matrix, the position of the eye in vecEye and the light vector in vecLightDir from the application.
In the vertex shader, the viewer vector V is calculated by subtracting the vertex position in world space from the eye position. The vertex shader outputs the position, the light, normal and viewer vector. The vectors are also the input values of the pixel shader.
All three vectors are normalized with normalize() in the pixel shader, whereas in the previous example vectors were normalized in the vertex shader. Normalizing vectors in the pixel shader is quite expensive, because every pixel shader version has a restricted number of assembly instruction slots available for use by the output of the HLSL compiler. If more instructions slots are used than available, the compiler will display an error message like the following:
error X4532: cannot map expression to pixel shader instruction set
The number of instruction slots available in a specific Direct3D pixel shader version usually corresponds to the number of instruction slots available in graphics cards. The high-level language compiler can not choose a suitable shader version on its own, this has to be done by the programmer. If your game will targets something other than the least common denominator of graphics cards on the target market, several shader versions must be provided.
Here is a list of all vertex and pixel shader versions supported by DirectX 9.
Version | Inst. Slots | Constant Count |
====== | ======== | =========== |
vs_1_1 | 128 | at least 96 cap'd (4) |
vs_2_0 | 256 | cap'd (4) |
vs_2_x | 256 | cap'd (4) |
vs_2_sw | unlimited | 8192 |
vs_3_0 | cap'd (1) | cap'd (4) |
ps_1_1 - ps_1_3 | 12 | 8 |
ps_1_4 | 28 (in two phases) | 8 |
ps_2_0 | 96 | 32 |
ps_2_x | cap'd (2) | 32 |
ps_3_0 | cap'd (3) | 224 |
ps_3_sw | unlimited | 8192 |
(1) D3DCAPS9.MaxVertexShader30InstructionSlots
(2) D3DCAPS9.D3DPSHADERCAPS2_0.NumInstructionSlots
(3) D3DCAPS9.MaxPixelShader30InstructionSlots
(4) D3DCAPS9.MaxVertexShaderConst
The capability bits above have to be checked to obtain the maximum number of instructions supported by a specific card. This can be done in the DirectX Caps viewer or via the D3DCAPS9 structure in the application. Checking the availability of specific shader versions is usually done while the application starts up. The application can then choose the proper version from a list of already prepared shaders or the application can put together a shader consisting of already prepared shader fragments with the help of the shader fragment linker.
Note that the examples shown here require mostly pixel shader version 2.0 or higher. With some tweaking, some of the effects might be implemented with a lower shader version by trading off some image quality, but that's out of the scope of this article.
The pixel shader example above calculates the diffuse reflection in the source code line below the lines that are used to normalize the input vectors. The function saturate() is used here to clamp all values to the range 0..1. The reflection vector is retrieved by re-using the result from the diffuse reflection calculation. To get the specular power value, the function pow() is used. It is declared as pow(x, y) and returns xy. This function is only available in pixel shaders >= ps_2_0. Getting a smooth specular power value in pixel shader versions lower than ps_2_0 is quite a challenge (read more at [Beaudoin/Guardado], [Halpin]).
The last line that starts with the return statement corresponds to the implementation of the lighting formula shown above.
Self-Shadowing Term

Figure 10. Self-shadowing term. (Image on right is very faint.)
It's common to use a self-shadowing term together with a specular lighting model to receive a geometric self-shadowing effect. Such a term sets the light brightness to zero, if the light vector is obscured by geometry and allows a linear scaling of the light brightness. This helps to reduce pixel popping when using bump maps. The screenshot in Figure 10 shows an example of a self-shadowing term on the right and an example that does not use a self-shadowing term on the left.
There are several ways to calculate this term. The following example uses (read more at [Frazier]):
S = saturate(4 * N.L)
This implementation just re-uses the N.L calculation to calculate the self-shadowing term. This leads to the following lighting formula:
I = A + S * (D * N.L + (R.V)n)
The self-shadowing term reduces the diffuse and specular component of the lighting model to null, in case the diffuse component is null. In other words: the diffuse component is used to diminish the intensity of the specular component. This is shown in the following pixel shader:
// I = ambient + shadow * (Dcolor * N.L + (R.V)n) | ||
|
Bump Mapping
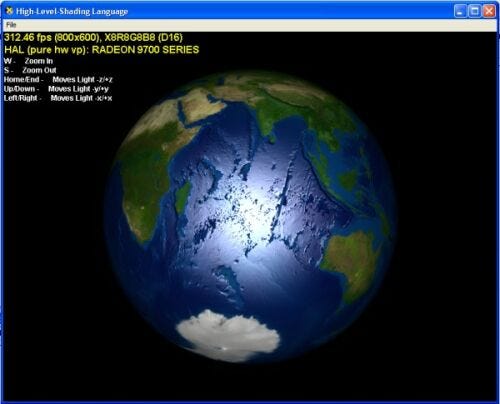
As you are probably aware, bump mapping fakes the existance of geometry (grooves, nodges, bulges). The screenshot in Figure 11 shows an example of a program that gives the viewer the illusion that regions with mountains are higher than the water regions on earth.
| ||
Figure 11. Bump mapping. |
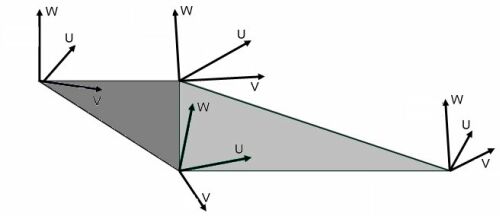
Whereas a color map stores color values, a bump map is a graphics file (*.dds, *.tga etc.) that stores normals that are used instead of the vertex normals to calculate the lighting. These normals are stored in the most common bump mapping technique in what is called texture space or tangent space. The light vector is usually handled in object or world space, which leads to the problem, that the light vector has to be transformed into the same space as the normals in the bump map, to obtain proper results. This is done with the help of a texture or tangent space coordinate system.
| ||
Figure 12. Texture space coordinate system. |
The easiest way to obtain such a texture space coordinate system is to use the D3DXComputeNormal() and D3DXComputeTangent() functions provided with the Direct3D utility library Direct3DX. Source code implementations of the functionality covered by these functions can be found in the NVMeshMender library, that can be downloaded from the Nvidia web site (developer.nvidia.com). Calculating a texture space coordinate system can work similar to the calculation of the vertex normal. For example, if a vertex shares three triangles, the face normal/face tangent of each triangle is calculated first, then these face normals of all three triangles are added together at the vertex that connects these triangles to form the vertex normal/vertex tangent. This example uses the vertex normal instead of a W vector for the texture space coordinate system and calculates the U vector with the help of the D3DXComputeTangent() function. The V vector is retrieved by calculating the cross product of the W and the U vector. This is done with the cross() function in the vertex shader:
struct VS_OUTPUT VS_OUTPUT VS(float4 Pos : POSITION, float2 Tex : TEXCOORD, float3 Normal : NORMAL, float3 Tangent : TANGENT ) Out.Light.xyz = mul(worldToTangentSpace, vecLightDir); // L float4 PS(float2 Tex: TEXCOORD0, float3 Light : TEXCOORD1, return 0.2 * color + shadow * (color * diff + spec); | ||
|
The 3x3 matrix, consisting of the U, V and W (== N) vectors, is created in the vertex shader and is used there to transform L and V to texture space.
Compared to the previous example, the major differences in the pixel shader are the usage of a color map and a bump map, that are fetched with tex2D(). The function tex2D() is declared as tex2D(s, t), whereas s is a sampler object and t is a 2D texture coordinate. Please consult the DirectX 9 documentation for a lot of other texture sampler functions, like texCUBE(s, t), which fetches a cube map.
The normal from the bump map is used instead of the normal from the vertex throughout the whole pixel shader. It is fetched from the normal map by biasing (- 0.5) and scaling (* 2.0) its values. This has to be done, because the normal map was stored in a unsigned texture format with a value range of 0..1 to allow older hardware to operate correctly. Therefore the normals have to be expanded back to their signed range.
Compared to previous examples, this pixel shader restricts the region where a specular reflection might happen to the water regions of the shown earth model. This is done with the help of the min() function and a gloss map that is stored in the alpha values of the color map. min() is defined as min(a, b) and it selects the lesser of a and b.
In the return statement, the ambient term is replaced by an intensity-decreased color value from the color map. This way, if the self-shadowing term reduces the diffuse and specular lighting component, at least a very dark Earth is still visible.
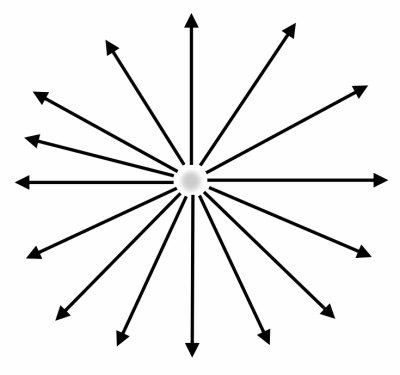
Point Light
The last example adds a per-pixel point light to the previous example. Contrary to the parallel light beams of a directional light source, the light beams of a point light spread out from the position of the point light uniformerly in all directions.
| ||
Figure 13. Point light. |
Using a point light with an attenuation map is extensively discussed in articles by Sim Dietrich [Dietrich2], by Dan Ginsburg/Dave Gosselin [Ginsburg/Gosselin], by Kelly Dempski [Dempski] and others.
Sim Dietrich shows in his article, that the following function delivers good enough results:
attenuation = 1 - d * d // d = distance
which stands for
attenuation = 1 - (x * x + y * y + z * z)
Dan Ginsburg/Dave Gosselin and Kelly Dempski divide the squared distance through a constant, which stands for the range of distance, in which the point light attenuation effect should happen:
attenuation = 1 - ((x/r)2 + (y/r)2 + (z/r)2)
The x/r, y/r and z/r values to the pixel shader via a TEXCOORDn channel and multiply them there with the help of the mul() function. The relevant source code to do this is:
// point light float4 PS(float2 Tex: TEXCOORD0, float3 Light : TEXCOORD1, // colormap * (self-shadow-term * diffuse + ambient) + self- | ||
|
Decreasing the LightRange parameter increases the range of light, whereas increasing this value leads to a shorter light range. The attenuation value is multiplied with itself in the pixel shader because this is more efficient than using the exponent 2. In the last line of the pixel shader, the attenuation value is multiplied with the result of the lighting computation to decrease or increase light intensity depending on the distance of the light source.
Wrapping Up
This article had covered the syntax and some of the intrinsic functions of HLSL by showing how to implement some common lighting formulas. It introduced you to six working (and generally concise) code examples, getting you ready to generate your own shaders. To move on from here, I recommend lurking into the RenderMonkey examples on ATI's web site and playing around with the source code found there. An interactive RenderMonkey tutorial can be found on my website.
Furthermore, two books on shader programming (in the "ShaderX2" series) will be published by Wordware in August 2003. These books contain articles about shader programming by over 50 authors, and cover many aspects of shader programming (more info can be found at http://www.shaderx2.com/). In a few weeks, Ron Fosner will publish an article on HLSL programming on Gamasutra that covers the use of RenderMonkey and Oren-Nayar Diffuse lighting. If you have any comments regarding this article, I appreciate any feedback -- send it to me at [email protected].
Acknowledgements
I have to thank the following people for proof-reading this text and sending me comments (in alphabetical order):
· Wessam Bahnassi
· Stefano Cristiano
· Ron Fosner
· Muhammad Haggag
· Dale LaForce
· William Liebenberg
· Vincent Prat
· Guillermo Rodríguez
· Mark Wang
This text is an excerpt from the following upcoming book:
Wolfgang F. Engel, Beginning Direct3D Game Programming with DirectX 9 Featuring Vertex and Pixel Shaders, May 2003, ISBN 1-93184-139-X
References
[Beaudoin/Guardado] Philippe Beaudoin, Juan Guardado, A Non-Integer Power Function on the Pixel Shader (This feature is an excerpt from Direct3D ShaderX: Vertex and Pixel Shader Tips and Tricks, edited by Wolfgang Engel)
[Dempski] Kelly Dempski, Real-Time Rendering Tricks and Techniques in DirectX, Premier Press, Inc., pp 578 - 585, 2002, ISBN 1-931841-27-6
[Dietrich] Sim Dietrich, "Per-Pixel Lighting", Nvidia developer web-site.
[Dietrich2] Sim Dietrich, "Attenuation Maps", Game Programming Gems, Charles River Media Inc., pp 543 - 548, 2000, ISBN 1-58450-049-2
[Foley] James D. Foley, Andries van Dam, Steven K. Feiner, John F. Hughes, Computer Graphics - Principles and Practice, Second Edition, pp. 729 - 731, Addison Wesley, ISBN 0-201-84840-6.
[Foley2] James D. Foley, Andries van Dam, Steven K. Feiner, John F. Hughes, Computer Graphics - Principles and Practice, Second Edition, p. 730, Addison Wesley, ISBN 0-201-84840-6.
[Fosner] Ron Fosner, Real-Time Shader Programming, Morgan Kauffmann, pp 54 - 58, 2003, ISBN 1 - 55860-853-2
[Frazier] Ronald Frazier, "Advanced Real-Time Per-Pixel Lighting in OpenGL", http://www.ronfrazier.net/apparition/index.asp?appmain=research/
%20advanced_per_pixel_lighting.html
[Ginsburg/Gosselin] Dan Ginsburg/Dave Gosselin, "Dynamic Per-Pixel Lighting Techniques", Game Programming Gems 2, Charles River Media Inc., pp 452 - 462, 2001, ISBN 1-58450-054-9
[Halpin] Matthew Halpin, "Specular Bump mapping", ShaderX2 - Shader Tips & Tricks, Wordware Ltd. August 2003, ISBN ??
[Mitchell/Peeper] Jason L. Mitchell, Craig Peeper, "Introduction to the DirectX 9 High Level Shading Language", ShaderX2 - Shader Programming Introduction & Tutorials, Wordware Ltd., persumably August 2003, ISBN ??
[RTR] Thomas Möller, Eric Haines, Real-Time Rendering (Second Edition), A K Peters, Ltd., p 73, 2002, ISBN 1-56881-182-9.
[RTR2] Thomas Möller, Eric Haines, Real-Time Rendering (Second Edition), A K Peters, Ltd., pp 35 - 36, 2002, ISBN 1-56881-182-9.
[Persson] Emil Persson, "Fragment level Phong Illumination", ShaderX2 - Shader Tips & Tricks, Wordware Ltd. Autumn 2003,
[Savchenko] Sergei Savchenko, "3D Graphics Programming Games and Beyond", SAMS, Seite 266, 2000, ISBN 0-672-31929-2.
[Valient] Michal Valient, "Advanced Lighting and Shading with DirectX 9", ShaderX2 - Shader Programming Introduction & Tutorials, Wordware Ltd., August 2003.
______________________________________________________
Read more about:
FeaturesAbout the Author(s)
You May Also Like