Complex Matrix Transformations

Matrix transforms are a ubiquitous aspect of 3D game programming. Yet it is surprising that game programmers do not often use a rigorous method for creating them or a common way of discussing them. Practitioners in the field of Robotics have mastered them long ago but these methods haven't made their way into daily practice among game programmers. Some of the many symptoms include models that import the wrong way and characters that rotate left when they are told to rotate right. So after a review of matrix conventions and notation, we'll introduce a useful naming scheme, a shorthand notation for transforms and tips for debugging them that will allow you to create concatenated matrix transforms correctly in much shorter time.

Matrix Representation of Transforms

Matrices represent transforms by storing the vectors that represent one reference frame in another reference frame. Figure 1 shows two 2D reference frames offset by a vector T and rotated relative to each. To represent frame one in the space of frame zero , we need the translation vector T, and the unit axis vectors X1 and Y1 expressed in the zero frame.

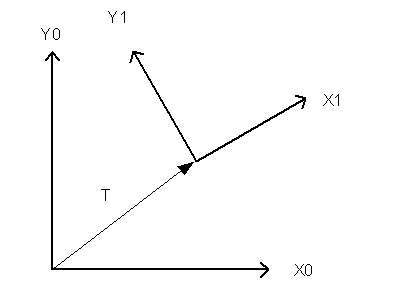
Figure 1: 2D Reference Frames offset and rotated from each other

We know that we need to store vectors in a matrix but now we have to decide how. We can either store them in a square matrix as rows or as columns. Each convention is shown below with the vectors expanded into their x and y components.

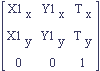
Figure 2: 2D Transform Stored as Columns

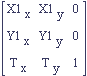
Figure 3: 2D Transform Stored as Rows

Each stores the same information so the question of which one is better will not be discussed. The difference only matters when you use them in a multiplication. Matrix multiplication is a set of dot products between the rows of the left matrix and columns of the right matrix. Figure 4 below shows the multiplication of two 3x3 matrices, A and B.

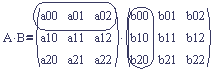
Figure 4: The First Dot Product in a Matrix Multiply

The first element in the product A times B is the row (a00, a01, a02) dotted with the column (b00, b10, b20). The dot product is valid because the row and the column each have three components. This dictates how a row vector and a column vector are each multiplied by a matrix.

A column vector must go on the right of the matrix.

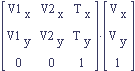
A row vector must go on the left of the matrix.

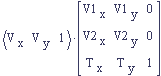
In each convention, the vectors are represented consistently as rows or columns as one might expect but it is important to realize that the order changes. Again, we must switch the order because the rows on the left must be the same size as the columns on the right in order for the matrix multiplication to be defined.

You can convert between row and column matrices by taking the matrix transpose of either matrix. Here we show that the transpose of a column matrix is a row matrix.

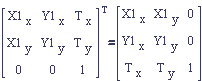
A Naming Scheme for Transform Matrices

In the first section we defined a matrix transform (figures 2 and 3) from reference frame 1 to reference frame 0 by expressing the vectors of frame 1 in frame 0. Let's name it M1to0 to make the reference frames it transforms between explicit. When we start to introduce new reference frames, as in figure 5, this name will be very handy.

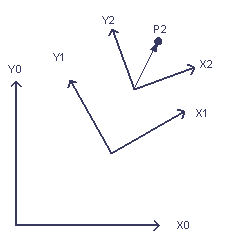
Figure 5: Introducing a third reference frame (2) and a point P2 in that frame.

These frames could represent the successive joints of a robot arm or an animation skeleton. Suppose the problem is to find P2 in the space of the zero frame. We'll call this point P0. We can now write out the answer to this problem using our naming scheme for matrices, keeping in mind the order of multiplication between row vectors and matrices and column vectors and matrices.

Column Convention

Substituting P1 into the equation for P0:

We have been consistent with the way column vectors are multiplied with matrices by keeping the column vectors to the right of the transform matrices.

Row Convention

We have been consistent with the way row vectors are multiplied with matrices by keeping the row vectors to the left of the transform matrices.

So the problem has been reduced to finding the transform matrices, and already we have accomplished a lot. We established a convention for naming points in space by the reference frame that they are in (P0, P1). We named matrices for the reference frames that they transform between (M1to0, M2to1). And finally, we leveraged the naming scheme to write out a mathematical expression for the correct answer. There is no ambiguity regarding the order of the matrices or which matrices we need to find.

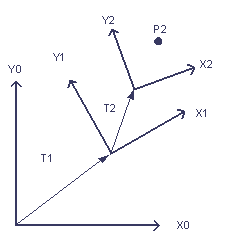
Figure 6: Reference Frames with T offset vectors shown.

Figure 6 shows the translation vectors between the frames. With the new information in the figure, we can plug into the matrices from figures 1 and 2 to get the needed transform matrices.

Column Convention

P0 = M1to0 * M2to1 * P2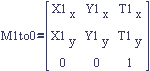

  

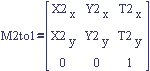
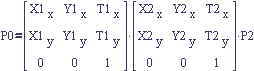
Row Convention

P0 = P2 * M2to1 * M1to0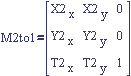

  

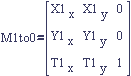
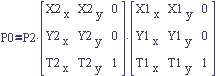
Thus we have solved the problem of finding point P0 given P2.

If we reversed the problem and needed to find point P2 given point P0 we could solve it using the same method. We would quickly find that we need the matrices M0to1 and M1to2 and we can get them using matrix inversion.

Again, we write the equation for P2 given P0, M1to0, and M2to1 by allowing the naming scheme to guide the order of the matrix concatenation.

Another way to write those equations is by multiplying the matrices first. Matrix multiplication is not communative (meaning you can't switch the order of the factors) but it is associative (meaning you can regroup the factors with parentheses). We can take the row equation:

And group the matrices together to illustrate the naming scheme for concatenated matrices.

So when multiplying matrices together using this naming scheme you just chain the reference frame names together.

These matrix derivations make excellent comments in the code that can save the person who reads your code lots of time.

Simplified Math Notation for Matrix Concatenations

The following is the component wise matrix multiplication for two 3x3 matrices and it is big.

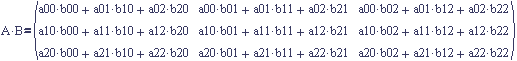
The multiplication of two 4x4 matrices is even bigger. It is already a large bulky expression with just two matrices. No one ever gained any insight into matrix concatenation of transform matrices by looking at the product expressed by each component. Instead we'll substitute algebraic variables for the sections of a transform in order to come up with a much more intuitive notation.

These are the components of a 4x4 column transform matrix:

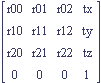
The upper left 3x3 portion is a rotation and the far right column forms the translation. Let's simplify the matrix by making some definitions.

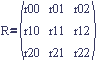
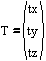
Now we can represent the 4x4 matrix as a 2x2 matrix^:

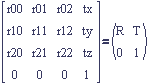
Working with 2x2 matrix multiplication is much easier.

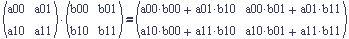
It is easy enough to do by hand. It is just four dot products between the rows on the left and the columns on the right. In the coming notation, many of the multiplications will be with one or zero so that will make it even easier.

Up to this point, we haven't dealt with scale but it is easy enough to add.

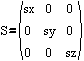
This new notation allows us to study the effects of combining rotation, translation, and scale by combining building blocks for each one. Figure 7 defines a 2x2 rotation matrix that is really a representation of a 4x4 transform matrix. Likewise, Figure 8 defines a 2x2 scale matrix that represents a 4x4 transform matrix.

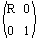
Figure 7: A 2x2 rotation matrix that represent a 4x4 transform

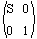
Figure 8: A 2x2 scale matrix that represents a 4x4 transform

This notation is not concerned with whether R has rows or columns in it so the R matrix (Figure 7) is the same in both row and column conventions. S is a diagonal matrix so its 2x2 matrix (Figure 8) is the same in both row and column conventions. The 2x2 matrix for translation must change based on the row/column convention to reflect the location of the translation in the full 4x4 transform.

Column Convention (T is a column):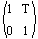

Row Convention (T is a row):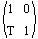

Figure 9: 2x2 Translation matrix that represents a 4x4 transform

Now we have the building blocks and we can start combining them. Let's start with a simple translation and rotation, change the order of multiplication and see what we can learn from it.

Column Convention

With translation on the left and rotation on the right we get the familiar M1to0 matrix, represented as a 2x2.

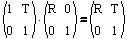
Switching the factors yields an entirely different result. The rotation, R, is the same, but the translation portion of the right hand side shows that R has rotated the translation.

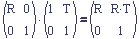
Row Convention

In order to get the familiar M1to0 row matrix, we need to put rotation on the left of the translation.

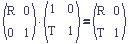
The other way around results in a rotated translation.

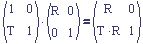
Now that the differences in the notation between row and column conventions have been shown, we'll only show the column convention to avoid repeating the same point.

The column transform for figure 6 is shown below. The change is that we have to distinguish between the different rotations and translations by naming them differently with subscripts.

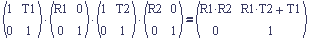
Now we experiment with scale. If we tack a scale matrix factor on the right of the product we get:

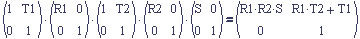
Right away you can see that the scale does not affect the translation (upper right portion of the product) at all because S doesn't appear in it. This makes sense because with columns, the full transform equation with points P0 and P5 included would look like this,

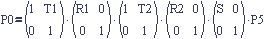
and it is just as though P5 was scaled and then the rest of the transform occurred afterwards. The given point was named P5 because each matrix is considered a transform from one space to another.

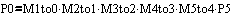
If the scale is introduced on the left,

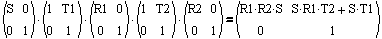
then every term in the result is scaled, as you might expect. There are countless combinations to explore. The notation makes it easier to form a complex transform from intuitive simple pieces.

It is easy to multiply 2x2 matrices by hand but it gets very tedious to repeat. Instead, you can enter any of the above symbolic expressions into Mathematica, MathCad, or Maple V and the product is computed for you. Math programs take some effort to learn but your investment will be paid back many times over.

Interpreting Concatenated Matrix Transforms

Transforms are described in steps made up of translations, scales, and rotations. There is sometimes confusion though about which step is first. The problem is that there are two valid ways of interpreting a transform. You can think of a transform as progressing from right to left with a point, P, being transformed from distant reference frames towards the zero frame. One might describe the following matrix transform as "P4 is rotated by R2, translated by T2, rotated by R1 and then translated by T1."

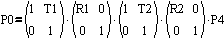
One can also describe the transform as a series of changes applied from left to right. Each change is applied to a reference frame. It would then be described as, "Starting with the zero frame, the axes are translated by T1, rotated by R1, translated by T2 and then finally rotated by R2." The former description mentions a rotation by R2 as the first step. The latter description mentions a translation by T1 as coming first so it can be confusing.

The right to left interpretation is obviously valid because you just start at the right and multiply your column vector by the right most matrix. At each step you get a column vector in another reference frame. The other interpretation is valid because you can imagine combining matrices from left to right. After each multiplication, you have a product matrix that can be partitioned into axis vectors and a translation, just like in Figure 2.

If you run into a discrepancy with someone about the way to read a matrix, write it out and discuss the pieces of the transform. The matrix math is the same regardless of the way it is read. You might each be talking about the same matrix but in two different ways.

Learning Your Company's Matrix Conventions

C++ has been so widely accepted by game developers that by now everyone that wants a matrix class already has one. Chances are your thoughts on whether row or column matrices are better are irrelevant because the company's (or team's) matrix class already exists and you have to use it. The task now is to make sure that you learn the company's matrix conventions. This includes the way the matrix elements are stored, and the decision to form row or column matrices. You could ask another developer or you could take a look at the way a matrix is multiplied with a vector in the matrix class implementation. Look at the dot product performed to reach the first element in the matrix product. If the vector is dotted with the top row of the matrix, the vector is a column. If the vector is dotted with the left most column, then the vector is a row. Next do a sanity check with some other functions. For instance, if there is a function that converts a quaternion to a matrix, check that it is following the same convention. Look up the conversion in a reference and check that the reference author agrees with the author of your class. After you are sure of the class conventions you won't ever have to question what they are again.

Debugging Matrix Concatenations

There is a bad but accepted method of creating matrix transforms amongst many game programmers that goes like this. Make an initial guess of what the transform expression might be and type it in. Try it out and see if it works. If it doesn't work, transpose and swap matrices in the expression until it works. This is exactly what not to do.

Instead, you should write out the expression for your matrix transform and know that it is right. You know it is right because you know your matrix conventions, and you used the above matrix naming scheme to create the expression. Of course there will be times when you have the correct expression but it doesn't work when you try it in code. When that happens you have to check that the matrices you created actually match their names and you have to check the matrices that were passed in from other sources as well. It can still be difficult but at least you will be progressing towards the right answer by isolating the problem.

The reason it is so important not to mechanically transpose or swap your matrices is that it is easy to get lost in all the possible transposes. We've seen that the difference between row and column matrices is a transpose. Unscaled rotation matrices have the property that their inverse is their transpose. So if you blindly invert a matrix you can be introducing a transpose. With enough swapping and transposing, you can get back to where you started because of the matrix identity:

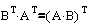
It is easy to get lost in all the transposes after only a few hacks. Another difficulty is that two transposes undo each other.

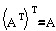
The iterative hacking of the matrix expression is supposed to stop when the result looks right but you may have two errors. This is why mysterious transposes live on in some code bases. After a while it would require a time consuming rigorous audit of too much code to fix. The best way to avoid those situations is to make the matrices correctly the first time.

Conclusion

We've covered several helpful ways to make creating transforms easier. Name vectors and points with the reference frame they are in. Name matrices by the reference frames that they transform between. Use the matrix names to guide the way they can be combined. Use the simplified 2x2 versions of the transforms to visualize and plan out your desired transform. And lastly, don't ever hack your transforms by swapping matrices or transposing them. If you follow these rules and get your fellow programmers to follow these rules, working with transforms becomes much easier.

References and Further Reading

The naming schemes, matrix concatenation, and the 2x2 transform notation was all covered in Prof. Lynn Conway's undergraduate Robotics course at the University of Michigan. Our course text had good coverage in a more rigorous manner:

Robotics for Engineers, Yoram Koren, McGraw-Hill, 1985., pp. 88-101. Unfortunately this book is out of print. Amazon occasionally has a used one.