Part 1

Introduction

It is said that the best suggestion on learning how to make video games is to go and make one. So we did. We started with a simple idea, with the main goal of developing a complete, interesting game while learning along the way and this is a kind of “post-mortem” developer diary on the challenges we faced and how we managed to solve them.

It will be an in-depth feature on our procedural level generation, analysis, and rating and will act as a companion piece to talks given at Codemotion 2012 in Rome (http://roma2012.codemotion.it/talk/skiddy-esperienza-un-primo-progetto-serio-nel-mondo-dei-videogiochi/index.html) and at Politecnico di Milano on October 31^st, 2014 (https://www.youtube.com/watch?v=8_UeywA68kA).

Those talks were design/gameplay oriented but they already presented a brief overview of our level creation system and tools.

Game Mechanics

Skiddy is a puzzle game where the aim is to lead all colored creatures to the matching color goal and clear the level. User input will move all non-static elements in any of the four directions until any obstacle is hit or according to their characteristics. Their movement cannot be altered while in motion.

Levels are composed of different block types laid out on grids of 5x4 to 8x7 cells.             

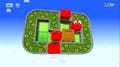
The outer border can only contain solid, unmovable Blocks, and Goals; the inner area of 3x2 to 6x5 can be filled with any other block except Goals.

Some of our available block types, grouped into 2 main categories:

Statics (they do not move regardless of input or other blocks interactions)

Moveable (they move either by player input or by interacting with other blocks)

All adjacent Skiddies will clear out in a combo when touching a goal.

3 Special medals are awarded for clearing a level in a set minimum number of moves (par), by completely clearing each color in a single move (max combo) or doing both at the same time (perfect!).

Hand-made levels

Initially Christian, the game designer, was plotting the first test levels by hand to define block behavior, interaction, goal conditions, and difficulty.

But while small levels with few blocks could still be completely reproduced on paper and solved with the mind, it was quickly apparent that the complexity was going to skyrocket on the way to define the 100 and more levels required for the easy game mode, and even worse for the hard mode.

We had no choice but to try to implement a tool to help us design, solve and analyze levels.

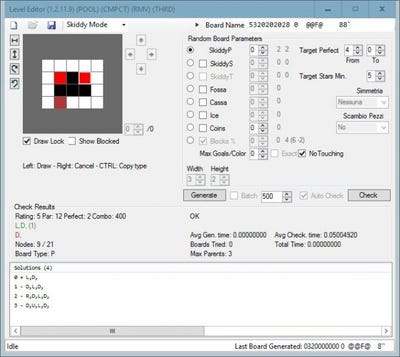
But what will be the limit of this tool? And can the tool tell us if a level is not only correct, but also good? What are the traits of a good level? Here’s how we found out.

Complexity problem

For the intent and purpose of level generation and analysis, blocks mechanics, once implemented correctly, are not important as long as it is understood that player input will take an existing board state and output a resulting state, with the game acting as a black box in the middle. This turns our game into a deterministic state machine with only 4 possible input (up, right, down, left), and a finite number of states S?

         player           block 
         input          mechanics
   S0    ------> [GAME] --------->    S?
Starting                           Resulting
 state                               state

Where:

S? == S0 if the received input will not change the level state.

S? == Sn if it’s a new, unique node.

S? == Sn’ if the resulting state was already created in a previous move.

As static blocks never change, each state S? is determined by the position of all the moveable blocks.

To verify that a level allows all winning conditions for the 3 medals to be obtainable, we also need to keep track of other information describing the game state at each Sn. Is this a Win state (all Skiddies cleared)? Is this a Combo state (always cleared each color in a single move)? And other conditions that will emerge later on, related to a level quality rating.

Even small levels can generate a lot of possible valid S? states, and the addition of a single piece can increase the complexity exponentially.

Level 1-1 in the game and its block representation: 3x2 moveable area. 2 Red Skiddies, 4 Empty Blocks, 1 Red Goal. This simple level contains the minimum number of blocks to fully show basic mechanics and allows one to gain all 3 medals.

Before we even start to think how to track these states, can we get an idea of how many states there will be in a level just looking at the available blocks? Statistics to the rescue!

This problem is a special case of distinguishable permutations of n objects, of which:

and the result is r = n!/n1!n2!n3!…nk! (the factorial of the total blocks divided by the product of the factorials of each type quantity).

In our case: n1==2; n2==4; r0 = (2+4)!/2!*4! == 6!/2*24 == 720/48 = 15

But this only gives us the result when BOTH red blocks are still in play, we must also consider the situation of a single block being cleared while the other remains in play! So we repeat the same formula for:

n1==1; n2==5; r1 = (1+5)!/1!*5! == 6!/1*120 == 720/120 = 6

And the final result is r01+r1 = 21

So a generalized formula for Skiddy becomes the sum of distinguishable permutations of n objects, where the distribution in n1 to nk must account for each block type (red, yellows, ice, etc..) to go from their starting quantity to 0;

In a 3x3 level with 2 couples of different colored Skiddies and 4 free blocks for example we have to calculate distinguishable permutations for

 n1 n2 n3
2  2  4    r0 = 420
2  1  5    r1 = 168
1  2  5    r2 = 168
2  0  6    r3 =  28
0  2  6    r4 =  28
1  1  6    r5 =  56
1  0  7    r6 =   8     
0  1  7    r7 =   8
r0 + r1 + …. + … r8  =  884 

but in the above level, possible game states are only 82.

Luckily this is only a theoretical ceiling, because game rules will not allow the generation of all these states, but we can get an interesting relation between potential complexity and real complexity.

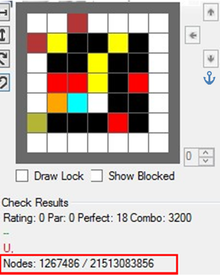Our generator will calculate potential and actual states as part of the level analysis and. Results for complex level gave us a ballpark for pre-allocation of states, to avoid excessive allocations/de-allocations while solving.

Here we can see that in a level with Crates, Ice cubes and 4 pieces per color, the situation can quickly get out of hand and even within the self-imposed limits of block combinations, later levels can reach EXTREMELY high potential states values.

In this case r = 21,513,083,856. Luckily real in-game states are ONLY 1,267,486, so let’s skip the diagram for this one, shall we?

Let’s analyze all potential and real states for level 1-1

Here we can see all game state generated by our moves. State 0 is how a level begins and is our root state. Moving in the 4 direction can either produce no result (0 -> Up -> 0), generate a new, unique state (0 -> Right -> 1) or generate a state we have already generated from a different state (1 -> left -> 3, but 3 was already generated from 0->left).

When a board is cleared of Skiddies we reach a Win state, so no further moves are necessary.

Win states where we achieve the Maximum Combo are marked with *Win*, otherwise the combo was broken in some previous move.

On this first level, only 9 unique states are possible, excluding win states.

These are all the 21 potential states we could create combining the available blocks (real games states are numbered as before).

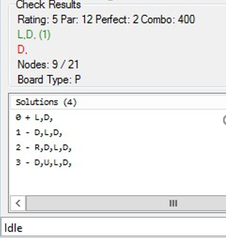
L1-1 Diagram

We correctly have 21 states (we don’t care about winning states) so this first level has a ratio of real to potential states of 9/21, as we can see in our editor.

Fair game

For the game to be fair and fun, we need to make sure that, as a minimal requirement, each possible game stat reachable by the player can still lead to the solution of the level. Otherwise we create a dead-end situation in which it is only possible to ping pong around and never solve the level or, even worse, get stuck in a single SN, both unacceptable conditions to be avoided in our final game levels.

 S0            S3

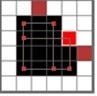
From S0 we move Down, Right, Up, 2 Skiddies will be cleared. We reach S3 and we are left with a single skiddy that can only move to the marked cells with no chance of ever reaching the goal. S3 is a Dead end state.

Continuing with the state machine analogy, it’s allowed to have cycles within our state transitions as long as one of these states is connected to a winning state.

But how do we need to keep track of all these states and check for correctness?

First strategy, a standard tree

We want to analyze all the effective states reachable while playing, so our generator will visit all the states in the same way we manually did in level1-1 analysis. At the same time we will keep track of all winning states to find all solutions, then verify that each unique state is part of a solution.

First let’s implement a game state node for analysis in a simplified, pseudo-C# code. For simplicity’s sake we assume all our moveable blocks can be encoded in an integer variable (with Skiddy we need 63 bit only for the blocks).

//The 3 possible node state according to our solvability check.
Enum NodeState {
      MaxCombo,    //node is part of a solution leading to the max combo
      Ok,          //node if part of a solution but the combo was broken
      DeadEnd      //node is not part of a solution
}

// A node contains information about board configuration and relations to other nodes
class Node {
      int Value;         //encodes our pieces’ layout and board score
      NodeState State;   //max-combo, ok or dead-end?
      ...
}

Starting from our root state, we will move in all 4 possible directions, create the 4 resulting child states and continue to analyze those. This could suggest us that a tree with 4 branch nodes could be the best way to represent our data, so we add the following fields to better define relationship between our nodes:

// A node contains information about board configuration and relations to other nodes
class Node {
      int Value;         //encodes our pieces’ layout and board score
      NodeState State;   //max-combo, ok or dead-end?
      ...
      Node[4] Child;     //the states originating from the next 4 moves
      int Index;         //tracks generating move(none, up, right, down, left)
                         //                       -1     0   1      2     3
}

We also have to keep track of 2 things duplicated states and winning conditions and, while we are looking for the shortest solutions, we want to catch nodes duplication at the shallowest depth, so we opt for standard breadth-first tree generation/traversal.

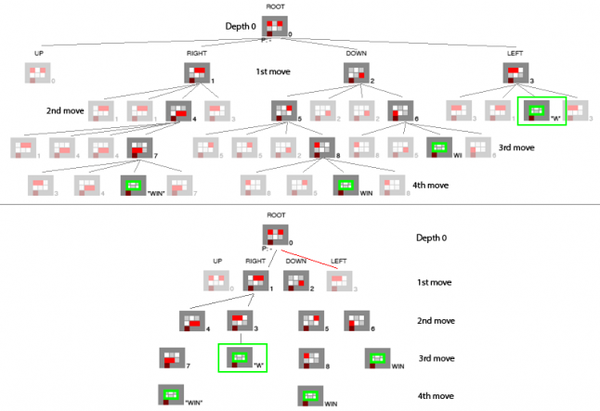
In the above diagram we see level 1-1 generated breadth first on top, depth first on the bottom (duplicated states are omitted). Differences are minimal but significant, and highlight why breadth first is an easier, better approach. In the highlighted depth-first example, when we continue from node 1 we meet S3 as a child (instead of being a-child of our root) since it hasn’t been discovered before, it is a valid unique node. When we proceed from S3, we reach the max combo win in 3 moves instead of 2. When later we try from the root to go left and encounter S3 again, it is now a duplicate. Depth first creates longer solutions.

When we reach a winning state, we need to transfer the notion of “we are part of the solution path” from the end node to the parent states, all the way up to our original starting root state.

So we can add a Parent field for easy backward-traversal of our tree

// A node contains information about board configuration and relations to other nodes
class Node {
      int Value;         //encodes our pieces’ layout and board score
      NodeState State;   //max-combo, ok or dead-end?
      Node[4] Child;     //the states originating from the next 4 moves
      int Index;         //tracks generating move(none, up, right, down, left)
                         //                       -1     0   1      2     3
      Node Parent;       //state before last move, used to traverse our solution
      ...
}

We set our winning state (either MaxCombo or Ok) and recourse back to the root, setting the correct state

//We can add this method to our Node class
void PropagateStateToRoot(NodeState state) {
      State = state;
      if (this != root) {                        //if we are not at the root node
             Parent.PropagateStateToRoot(state); //recursively call this on our
      }                                          //parent node
}

In the end the path from our root node to this winning node will be one of our solutions. If we take Level1-1 as an example:  root (S0) -> Left-> S3 -> Down -> Max combo Win.

At this point our root node, our S3 node and the winning node all have state == DeadEnd.

We set The final Node.State = MaxCombo; and, because (this != root), we call PropagateStateToRoot on the parent ( state3); we repeat and propagate to the root and stop.

While we do this we can also collect all our node indexes in a solution list, and collect all our solution lists in another list. Let’s define a tree class to manage this:

//a tree contains information about all our node, their relations, solution paths, etc.
Class Tree {
      Node Root;
      List<int> CurrentSolution;
      List<List<int>> Solutions;
}

And modify our Node’s method.

//We can add this method to our Node class
void PropagateStateToRoot(NodeState state) {
      State = state;
      if (this != tree.Root) {               //if we are not at the root node
             tree.CurrentSolution.Add(index);//add our move index to the current
                                             //solution;
            Parent.PropagateState(state);    //recursively call this on parent node
      } else {
             tree.Solutions.Add(ReverseSolution(CurrentSolution));
             //reverse the current solution as it was stored child->root but we
             //want it root->child and add it to our tree solutions list
      }
}

One remaining problem with this structure is that when we must verify that a node state is not pre-existing (to avoid getting stuck in a loop) we have to traverse the tree from root to children to finish every time.

Similar to our winning state propagation, we will see that most information in our state checking routine has a tendency to flow backward, from child nodes to parent nodes.

In part 2 we will revise our data structure to accommodate these characteristics and improve our level analysis.

Disclaimer: As a first experience in designing/programming a videogame, we are aware our methods might not be the best but they served the purpose and aided the design and the code to evolve and complement each other.

If readers have questions or suggestions regarding the subject matter and how to improve it, we at BigBangPixel would sincerely like to discuss it, so write us at [email protected]

License: Skiddy and all related assets including levels and editors are Copyright 2012 by BigBangPixel and all rights are reserved. The information published in this article can be used by anyone for non-assignable, non-transferable, non-commercial use or educational purposes.  Any other use, including any redistribution in whole or in part, requires explicit, written permission from BigBangPixel.