[This sponsored feature, part of Intel's Visual Computing site and written by Dr. Michael J. Gourlay of the University of Central Florida Interactive Entertainment Academy, continues a multi-part series that explains fluid dynamics and its simulation techniques. For the first instalment, please click here.]

Fluid Simulation Techniques

As explained in the previous article, non-linear partial differential equations (PDE's), combined with initial and boundary value constraints, describe the motion of fluids. Solving those equations is difficult; unlike simpler like ballistic trajectories or harmonic oscillations, fluid motion has no "closed-form" analytical solution. This article describes numerical techniques used to compute approximate solutions to fluid motion.

The difference between reality and simulation includes at least two aspects: approximation and discretization. The equations we write down are only approximations of reality. For example, the notion of "viscosity" oversimplifies the actual interactions between molecules. Also, fluids are continuous media, meaning that they exist at an infinite number of points in a region of space. Computer simulations convert the mathematical model of fluids from a continuum into a finite number of discrete values. Those values can reside in a mesh, or they can move freely as particles.

Recall from the previous article that to calculate fluid motion, you can solve for either momentum or vorticity. You can categorize fluid simulation techniques according to which equations they solve and according to their discretization scheme. This article presents the ideas behind these techniques:

Fluid simulations run slowly (in part) because of the need to use a large number of points to represent a continuum. You can speed up simulations by employing approximations (that is, trading realism for speed). You can also parallelize the computation and make use of multicore hardware, which is becoming increasingly prevalent. This article reviews some numerical techniques often employed to simulate fluid motion and mentions some ways in which you can parallelize numerical codes to use multi-core hardware.

Discretization

When solving fluid dynamics equations numerically, you convert the original continuous problem (which has infinite degrees of freedom) into a discrete problem (which has finite degrees of freedom). The choice of discretization scheme influences other aspects of the simulation, including interpolation, approximating spatial derivatives, evolving in time, and satisfying boundary conditions. That discretization process has many forms -- too many to cover here -- so this article focuses on intuitive formulations: Discretize space, approximate spatial derivatives using that discretization, and rewrite the continuous equations by replacing spatial derivatives with those approximations.

The previous article presented Eulerian (fixed-coordinate) and Lagrangian (moving-coordinate) views of the fluid momentum and vorticity equations. Analogously, you can discretize space using grids, particles, or a hybrid of the two. Regardless of whether they use grid-based or mesh-free discretization, we give the name nodes to locations where the simulation explicitly represents values.

Grid-based Discretization

Grid-based discretizations are useful for Eulerian views -- that is, treating fluids as fields whose properties the simulation tracks at specific locations. Deciding on a specific grid to represent a field is called meshing.

The simplest is a uniform fixed grid, as Figure 1a depicts: Divide space into cells at equal intervals along the axes of the coordinate system. This allows fast lookups, because you can directly compute the memory address of a grid cell based on its location in the virtual world. Uniform grids can, however, be wasteful; in a typical flow, some regions need very high resolution, but most can use low resolution. With a uniform grid, all regions have the same resolution, so they typically over-resolve some regions and under-resolve others.

Simulations can also use an adaptive grid, which provides high spatial resolution only where needed -- for example, where vortices form and near boundaries, as Figure 1b shows. Creating such a grid can be complicated, especially when boundaries move, such as when objects move in the fluid. Also, space-based lookups are slower for adaptive grids than for uniform grids, because they entail traversing more complicated spatial partitioning data structures.

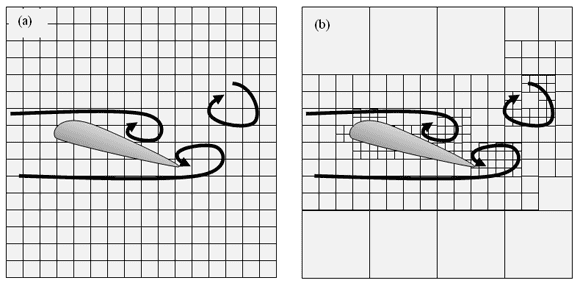
Figure 1: (a) A uniform fixed grid; (b) an adaptive grid

Recall from the previous article that certain governing equations describe fluid motion. Each equation describes the time evolution of a fluid property such as velocity and density. The recipe for a grid-based fluid simulation usually entails computing the terms of those governing equations and updating each of those properties at each grid point. Most of the effort lies in computing those terms and performing the update robustly, which this article delves into later. But in principle (if not in practice), the recipe is that simple.

If you want to know the value of a fluid property between grid points, you have to interpolate. You could use a variety of techniques to perform that interpolation, and this relates to how to compute spatial derivatives, which this article covers in more detail below.

Simulations using grid-based discretizations can suffer from unwanted numerical diffusion. You can understand this phenomenon by employing an analogy to image creation and processing. If you draw a diagonal line through a grid of pixels, you have to choose between making the line jagged or blurry: There is no way to represent a line exactly at every position along the line using a discrete grid. This problem worsens each time you move the line: After each update, it gets blurrier and noisier, as Figure 2 shows. Computer graphics applications prevent this incremental blur by storing and operating on idealized representations of lines (such as pairs of points). Computational fluid dynamics has a loosely analogous technique: store and operate on idealized fluid particles.

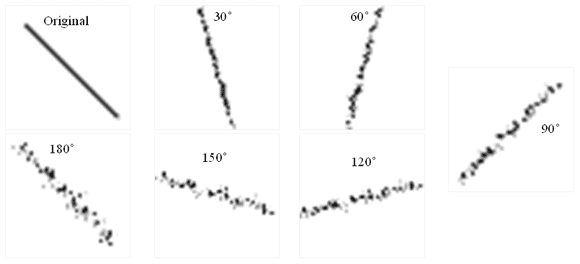
Figure 2: Numerical diffusion. The original line is rotated 180 degrees in increments.

Mesh-free Discretizations

In contrast to grid-based discretizations, mesh-free discretizations are useful for Lagrangian views -- that is, tracking the behavior of particles as they move with the flow. These particles can represent fluid properties such as position, density, velocity, and vorticity. Those properties never diffuse (unless you tell them to). Furthermore, the simulation can place more particles only where the flow requires higher resolution, so the simulation can (in principle) be more efficient.

Fluid particle simulations come in two major varieties: SPH and the discrete vortex method (DVM). SPH simulations use "fluid particles" to represent a flow field. Although it is tempting to think of these fluid particles as particles of fluid material, it is perhaps better to think of them as mobile clouds that move and carry fluid property information with them. The distinction is subtle but important. In mesh-free simulations, finding the value of a fluid property at any given location requires interpolating values between particles. Each particle represents a "source" in a smoothed, localized field. Figure 3a shows an example of a smoothing function that "spreads" the influence of a particle across a small region. The field could be any fluid property, such as density, temperature, or velocity. In order to find the value of the field at a given location, you include contributions to that field due to all particles in the vicinity of that location. Usually, several particles contribute to the field at each location. So, you would need to interpolate between particles, as shown in Figure 3b.

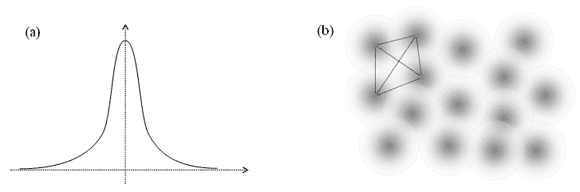
Figure 3: Smoothed particle discretization. (a) Smoothing function. (b) Several smoothed particles representing a field. Lines connect particles that would be used to interpolate the field in that region.

DVM simulations use vortex particles called vortons to represent tiny vortex elements, which represent swirling regions. Each of these particles induces a velocity field that circulates around the vorton, as shown in Figure 4. This induced velocity field extends outward to large distances. So, each vorton influences the motion of all other vortons in the fluid.

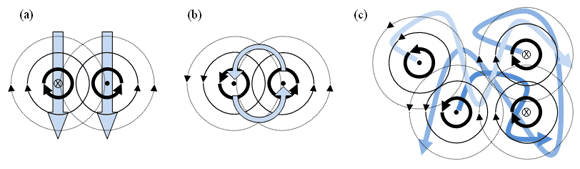
Figure 4: Vortex particles (vortons) and the velocity fields they induce. (a) Counter-rotating vortex pairs push each other along a line. (b) Co-rotating vortex pairs orbit each other. (c) Four or more vortices move each other chaotically.

The recipe for evolving a mesh-free fluid simulation has the same structure as in grid-based simulations, plus one extra step: advection. The first article in this series explained advection; each particle needs to move (following the flow) in addition to having its properties updated. The "update" step resembles the same step as in grid-based simulations; but the advection step differs substantially.

Computing advection in a vortex simulation requires special treatment, because the vorticity equation does not directly provide velocity but via the advection term directly requires velocity. (In contrast, the momentum equation both provides and requires velocity.) Computing advection in a vortex-based simulation therefore requires obtaining velocity from vorticity. The Biot-Savart law relates the vorticity 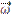of a vortex element at a displacement 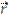to a point with velocity :

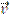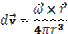
DVM simulations use this law to advect each vorton because of the influence of all other vortons.

If the simulation has N vortons, a straightforward advection computation would take O(N²) operations, which is too slow. So instead, you can approximate the influence of clusters of multiple distance vortices as a single vortex. As long as those clusters are far enough away, this approximation works well enough for visual effects. Figure 5 shows ways in which you can represent vortex clusters using hierarchical data structures (for example, trees). The bottom row of nodes represents actual vortons. In the layer above that, each node represents clusters of vortons, and the layer above that represents clusters of clusters, and so on. To compute the velocity at a query location, traverse the tree from top down, as Figure 5b shows: Visit each node and ask whether the query location (heavy oval) is inside the region that node represents. If not, apply the influence of that cluster (shaded regions) as though it were a single vorton. If the query location lies within the cluster region, then descend that branch (following the arrows) and repeat.

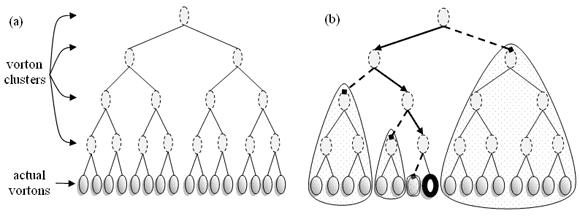
Figure 5: Vorton cluster tree. (a) Each ancestor node represents its descendents as a single vorton. (b) Traversal for finding clusters influencing the marked vorton.

In principle, vorton simulations can focus computational resources on areas of flow with the most interesting motion: regions with vorticity. Because it does not numerically diffuse vorticity, the technique works for low-viscosity flows -- for example, smoke from a fire -- where you want to retain fine-scale swirly motion over long durations. But the long-range advection interaction is either slow or complicated; there are no trivial, fast solutions.

You can combine elements of grid-based and particle-based simulations to get the best of both.

Hybrid Schemes

Eulerian approaches can suffer from instability because of the advection term (as explained below). One way to avoid the instability is to ask, for each grid point at each time step, from where did the flow arrive? This "backtracking" is called a semi-Lagrangian technique, because it treats advection similarly to particle-based methods.

Conversely, discrete vortex methods require either expensive or complicated algorithms (described above) to compute velocity. Instead of using the Biot-Savart law, you can transfer vorticity from particles to a grid and solve a vector Poisson equation to recover the velocity field. (Poisson solvers are readily available.) These so-called particle-in-cell (PIC) or vortex-in-cell (VIC) techniques also simplify computing spatial derivatives (discussed below). Meanwhile, the basis of the simulation remains in vortons, which do not diffuse, so VIC methods give you the relative simplicity of a grid-based method and the lack of diffusion of a particle method.

Numerical Methods

Numerical methods used in fluid simulation include interpolating values between nodes, approximating spatial derivatives, solving differential equations to evolve flow through time, and satisfying boundary conditions.

Interpolation

You need to be able to determine values at locations other than nodes where the simulation explicitly represents them. You do so using interpolants, also called basis functions, which pass through nodes.

You can choose among a variety of interpolating functions, from local to global. Piecewise line segments provide linear interpolation between adjacent gridpoints (Figure 6a). Instead of using only the immediately adjacent points, you can also use a broader neighborhood of gridpoints and a higher-order interpolant such as a piecewise cubic spline (Figure 6b). Taking that line of thought to its logical conclusion, you can use a much higher-order function to create a spline that spans the entire domain (Figure 6c).

Figure 6: Interpolation on a grid. (a) Linear. (b) Cubic. (c) Global.

Particle simulations can track nearest-neighbors (as a portion of Figure 3b shows) and use interpolation techniques specialized for irregular data. Spatial partitions such as octrees and kd-trees organize particles that reside in the same physical neighborhood to also reside in the same data neighborhood. You can then search the resulting tree for the nearest neighbors of a given location.

Alternatively, you could use a hybrid PIC approach; use particles to represent fluid properties, transfer values from particles to a grid, and use grid-based techniques to interpolate those properties in the regions between particles.

Spatial Derivatives

The equations governing fluid motion include terms involving spatial derivatives, so you need to compute those. The techniques to approximate spatial derivatives relate directly to the interpolation techniques.

Finite difference (FD) methods use differences of quantities from adjacent locations divided by their separation (as shown in Figure 7). Because they use only local information, FD methods readily handle arbitrary, changing boundaries (for example, moving bodies in the fluid) but have low accuracy compared to other techniques. FD is simple, flexible, and effective and so is a good choice for video games, where accuracy is not paramount.

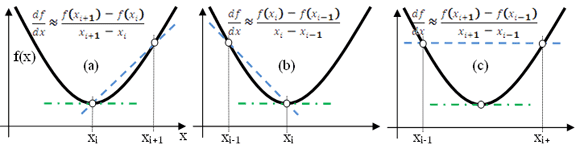
Figure 7: Finite differences. (a) Forward, (b) backward, and (c) centered.

Spectral methods use interpolating functions spanning multiple values in the domain, and you can compute derivatives of those functions analytically. Spectral methods offer higher accuracy but because they use global (or less local) information, the domain shape and boundary conditions impose constraints that determine which functions work well to represent the flow field.

These techniques to approximate spatial derivatives equip you with the ability to compute each term in the governing equations.

By replacing derivatives in the continuous equations with approximation, you convert the continuous equations with a discretized form. When using FDs, this means the continuous PDE's change into a system of linear algebraic equations. For example, replacing the gradient 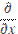with a centered difference, the continuous equation

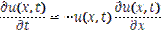
becomes the spatially discrete equation

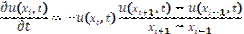
After plugging approximated spatial derivative values into the original fluid dynamics equations we must also discretize those equations in time to create an algorithm to update the simulation for each new step in time.

Time evolution

Simulations evolve forward in time in discrete steps. Time evolution schemes include families of explicit and implicit techniques that have various accuracy and stability properties. The most straightforward scheme entails explicitly and directly integrating values forward in time, given information about previous times. The same schemes apply to ordinary differential equations used to simulate particle and rigid body motion.

Explicit methods solve for the future using information about the past. Varieties include Euler (Figure 8a), Runge-Kutta, and Midpoint (Figure 8b). The simplest method -- the forward Euler method -- is defined as

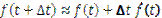
where 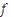is the quantity being evolved, 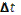is the time step, 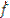is the first time derivative, and 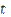is time. The forward Euler method is analogous to using a forward difference scheme (as in Figure 7a). The example PDE above, discretized in both time (using forward difference) and in space (using centered difference), becomes

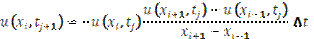
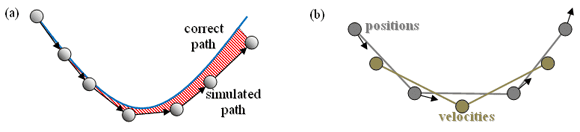
Figure 8: Explicit timestepping. (a) Explicit Euler. (b) Midpoint "leapfrog".

Applying this to each node i makes a system of linear algebraic equations. You could express that system of equations in matrix-vector form. The resulting matrix would be sparse (that is, have a lot of elements that are zero). Specialized linear algebra algorithms exist that exploit sparseness: You could use them to solve that system of equations.

Explicit methods are simple, but they can be tricky or slow to make stable. The Courant-Friedrichs-Lewy (CFL) condition establishes a relationship between spatial resolution and time step in some PDEs. Informally, this means that the time step must be smaller than the duration it takes for a bit of fluid to move from one grid cell to another (as Figure 9 shows). That implies that the faster the fluid motion, the smaller the time step, which implies more time steps, which implies more computational effort and a slower simulation.

If a numerical solution is unstable, errors grow rapidly without bound. One way to mitigate this is to damp out oscillations (for example, using viscosity). This prevents the solution from "exploding" but also restricts fluid motion to have high viscosity -- for example, syrup instead of water.

Semi-Lagrangian techniques (described above) avoid the instability by using a particle-based scheme to advect fluid (as Figure 9c depicts). The other terms of the fluid dynamics equations are computed using an Eulerian view. Backtracking dodges the instability even when fluid parcels move farther than a grid cell per time step.

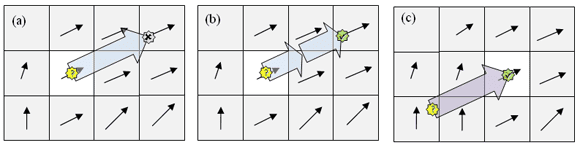
Figure 9: CFL condition. (a) CFL violated, (b) CFL satisfied with smaller timesteps, and (c) instability avoided using backtracking.

Implicit methods derive from writing the equations of motion so that the future solution depends on both future and past solutions. For example, the backward Euler method is defined as

This might seem absurd: You would apparently need to know the future to solve the problem. But in practice, it is possible to find a solution implicitly by using a numerical linear algebraic solver, such as Jacobi, Gauss-Seidel, successive over-relaxation (SOR), or conjugate gradient (CG). When using a finite difference discretization and its corresponding linear system of equations (described above), using an implicit scheme would only require changing the values in the linear algebraic system's matrix; the solver code would remain identical.

Implicit methods are often stable when explicit methods are not, even if the simulation apparently violates the CFL condition. But this stability comes with a cost: Effectively, the simulation becomes damped, behaving somewhat as though it cranked up viscosity. This phenomenon is called numerical viscosity. The final results might end up looking like those from an explicit solver with very high viscosity -- and the implicit solver can take more computational effort.

Interactions with Bodies: Boundary Conditions

Solving PDE's also entails satisfying boundary conditions, meaning that the flow must obey certain rules at boundaries. The previous article described canonical cases, and Figure 10 catalogs various boundary conditions.

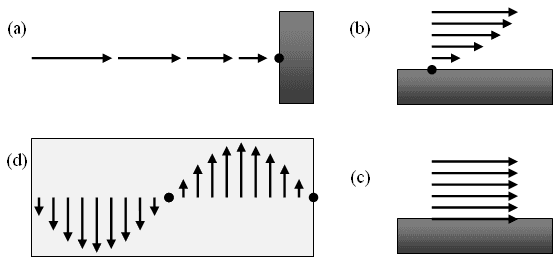
Figure 10: Boundary conditions. (a) No-through, (b) no-slip, (c) free-slip, and (d) periodic.

Simulations can satisfy boundary conditions either explicitly or implicitly. A simulation can explicitly satisfy boundary conditions either by incorporating them into the system of linear algebraic equations resulting from the discretization or by applying a post-process each step. The advection step can result in a preliminary solution that violates boundary conditions(for example, can have flow through or across a rigid body, which is physically impossible). Various techniques exist to resolve that problem. The simplest is to overwrite the fluid values at the boundaries and let the subsequent evolution steps propagate that change away. That treatment is not accurate but can suffice for visual effects. Be aware, though, that such abrupt changes can introduce instability to the simulation.

Alternatively, simulations can represent the solution in a way that it always satisfies boundary conditions. This can usually only be done in special cases -- for example, by using spectral methods where the interpolating functions have the desired values at boundaries. Such schemes are probably too restrictive for use in video games, which likely have objects with arbitrary (possibly changing) shape moving through the fluid.

Satisfying boundary conditions is, in principle, a two-way interaction. Bodies in the fluid affect the flow, and the flow also affects the bodies. In practice, this two-way coupling occurs in separate steps. The fluid simulation provides forces applied to rigid bodies immersed in the fluid either by computing the pressure gradient at the body surface or by using conservation of linear and angular momentum to compute impulses applied by fluid particles. Then, a separate rigid body simulator can apply those forces or impulses to the bodies and proceed as usual.

Parallelization

Using a localized physical model expedites parallelizing fluid simulation; any aspects of the simulation that require global solutions (that is, solutions that affect the entire simulation domain simultaneously) will impede parallelization. Sharing memory across threads simplifies parallelization. Distributed memory systems (such as the IBM CELL architecture) require more sophistication.

Particle-based methods readily parallelize, because you can update the motion of each particle independently from the others. Each particle could, in principle, run in its own thread. For vorton methods, this assumes that the interaction tree contains all the information needed from the original particles before updating any particles, which you can readily arrange.

Mesh-based methods readily parallelize for the same reason particle-based methods do: The simulation algorithm can update each cell independently. In practice, this entails using a numerical linear algebraic solver that stores the output in a different vector than the input, effectively double-buffering the data. Although this requires more memory, it makes parallelization easier. Note that this imposes some prejudice against the Gauss-Seidel method, which uses partially updated information during the solver; although that improves convergence speeds in a serial process, it creates contention in parallel processes.

Summary

Simulating fluid motion entails converting continuous equations into simpler discrete equations and using numerical techniques to solve the discretized equations. Spatial discretizations include grid-based and mesh-free methods. Simulations employ techniques for interpolating values between nodes, approximating spatial derivatives and evolving the simulation forward in time, meanwhile satisfying boundary conditions. Fluid simulations also provide the means to provide forces acting on bodies embedded in the fluid, which a separate rigid body simulator can apply.

The next article in this series presents a mesh-free vortex particle fluid simulation suitable for use in a video game.

Further Reading

Stam, J. (1999): "Stable Fluids", SIGGRAPH 99 Conference Proceedings, Annual Conference Series, August.

Cottet & Koumoutsakos (2000): Vortex Methods: Theory and Practice. Cambridge University Press.

Li & Liu (2004): Meshfree Particle Methods. Springer-Verlag.

Bridson (2008): Fluid Simulation for Computer Graphics.  A.K. Peters.